Основные понятия теории графов

Задача о замене оборудования

Задача оптимального распределения инвестиций

Инвестор выделяет средства в размере с усл. ед., которые должны быть распределены между m предприятиями. Каждое i -тое предприятие 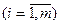при инвестировании в него 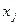средств приносит прибыль 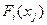усл. ед. Нужно выбрать оптимальное распределение инвестиций между предприятиями, обеспечивающее максимальную прибыль.

В данном случае речь идет об однократном распределении средств, и поэтому задача сама по себе не является динамической. Однако ее можно наиболее просто решить как многошаговую, если объекты капиталовложений включать в рассмотрение последовательно, то есть на каждом шаге к рассмотренным добавлять следующий.

Пусть имеются четыре предприятия, между которыми следует распределить 400 усл. ед. Получаемая предприятиями прибыль в зависимости от выделенной суммы 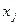представлена в таблице (объем инвестиций разбивается на N интервалов с шагом ):

Капитальные вложения	Предприятия

Целевая функция 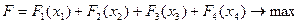при ограничениях .

Пусть 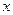– объем средств, выделяемых предприятиям, причем 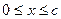; 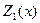– максимальная прибыль фирмы, если 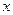средств выделить только первому предприятию; 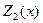– максимальная прибыль фирмы, если 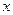средств разделить между первым и вторым предприятиями; 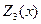– максимальная прибыль фирмы, если 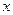средств разделить между первым, вторым и третьим предприятиями; 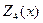– максимальная прибыль фирмы, если 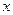средств разделить между всеми четырьмя предприятиями. При этом .

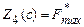Обратный ход. Рассмотрим финансирование только первого предприятия, тогда по определению

.

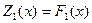Распределим средства в объеме 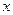между первым и вторым предприятиями: второму в объеме , тогда 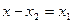выделяется первому, следовательно,

.

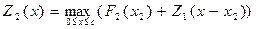Включим в рассмотрение третье предприятие: из общей суммы выделим третьему предприятию усл. ед., тогда остальная часть 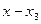оптимальным образом распределится между двумя первыми предприятиями:

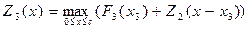. Аналогично, .

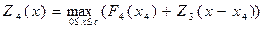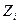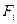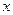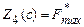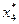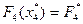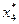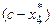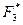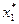Прямой ход. Полученные функциональные уравнения Беллмана позволяют рассчитать значения и для всех возможных . Среди них находим и оптимальное такое, что , после чего результаты вычислений просматриваются в обратном порядке. Зная , находим – объем финансирования остальных трех предприятий, а, следовательно, и и и т.д. до нахождения и .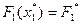

Произведем расчет.

Обратный ход. Составим расчетную таблицу значени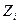й и 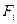, которая заполняется по столбцам:

x	Z1 = F1	F2	Z2	F3	Z3	F4	Z4

Элементы в столбцах для 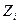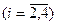находим по уравнениям Беллмана. Например,

.

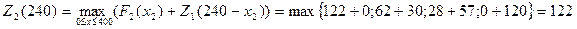Прямой ход.

Из таблицы следует, что 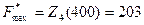(усл. ед.) и

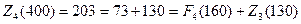, следовательно, четвертому предприятию следует выделить 160 усл. ед., то есть 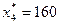. Тогда

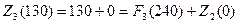, следовательно, , , .

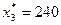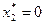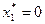Ответ: x ^* = (0; 0; 240; 160), 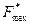= 203.

Таким образом, для получения максимальной прибыли в размере 203 усл. ед. следует 240 усл. ед. вложить в третье предприятие и 160 усл. ед. в четвертое, в первое и второе предприятия вкладывать не стоит.

Замечание 11.1. По расчетной таблице можно получить стратегию вложения средств, например, только в первые два предприятия, или вложение суммы в 240 усл. ед. во все четыре предприятия и т.д. Это так называемый «принцип погружения» метода динамического программирования.

В начале планового периода из N лет имеется оборудование возраста t лет. Для каждого года планового периода известны стоимость r (t) произведенной с использованием имеющегося оборудования продукции и затраты u (t), связанные с его эксплуатацией. Эти характеристики зависят от возраста t оборудования. Известны также остаточная стоимость S оборудования, не зависящая от его возраста, и цена р единицы нового оборудования, не меняющаяся в рассматриваемом плановом периоде. Требуется разработать оптимальную политику в отношении имеющегося оборудования, то есть в начале каждого года планового периода установить, сохранить в этом году оборудование или продать его по остаточной стоимости S и купить новое по цене р, с тем чтобы ожидаемая прибыль за N лет достигла максимальной величины.

Здесь шаг – год планового периода. Число шагов равно числу лет планового периода. Состояние системы характеризуется возрастом оборудования. В начале каждого шага может быть выбрано одно из двух управлений: «сохранение» или «замена» оборудования. Целевая функция за плановый период . Ограничения определяются критерием замены оборудования: прибыль при дальнейшей эксплуатации старого меньше прибыли после его замены с учетом всех издержек. Если прибыль от нового оборудования равна прибыли при старом, то старое сохраняется еще на год, так как оно уже досконально изучено.

Задача решается с помощью принципа оптимальности Беллмана. Рассмотрим годы планового периода от конца к началу (обратный ход). Введем последовательность функций 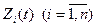– максимальная прибыль, получаемая от оборудования возраста t за последние i лет планового периода.

Здесь 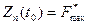, где t ₀ – возраст оборудования в начале планового периода.

Для последнего года оптимальная политика и максимальная прибыль 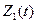находятся из условия:

– сохранение – замена

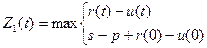
Рассмотрим прибыль за последние два года:

– сохранение – замена

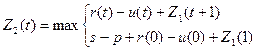
Аналогично, для i последних лет:

– сохранение – замена

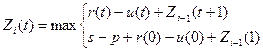
Для i = n: .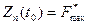

После этого остается пройти процесс в прямом направлении и сформулировать безусловную оптимальную политику в отношении имеющегося оборудования.

Для заполнения расчетной таблицы можно использовать следующий алгоритм:

1) Найти , .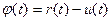

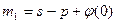2) Заполнить строку 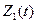, переписав из таблицы данных соответствующие значения 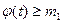, все значения 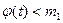заменить на .

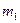3) Начиная с i=2, расчет по строкам производится в следующей последовательности:

а) вычислить 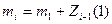, где 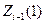берется из уже заполненной строки;

б) вычислить 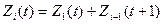, где сумма и слагаемые образуют треугольник, у которого одна из вершин всегда в первой строке над искомым значением, а вторая – в последней заполненной строке следующего столбца. Получаемые значения 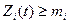вносить в соответствующие клетки строки, начиная с первого 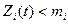, оставшиеся клетки строки заполнить значением ;

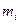в) клетки с первым значением 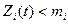в процессе заполнения таблицы отделить от расположенных в строке левее разделительной границей смены управления;

г) если таблица не заполнена до последней строки, перейти к пункту а) и выполнить расчет для следующего значения индекса i.

Задача. Пусть s = 2, p = 15, t ₀ = 4. Прибыль и издержки предприятия в зависимости от возраста оборудования заданы таблицей:

t
r (t)
u (t)
j (t) = r (t) – u (t)

Обратный ход.

Определим .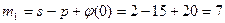

Заполним следующую таблицу по ранее указанному алгоритму:

Zi (t)/t								mi
Z 1(t)
Z 2(t)
Z 3(t)
Z 4(t)
Z 5(t)
Z 6(t)

Прямой ход.

Максимальная прибыль при оптимальной политике .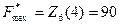

Эта клетка находится слева от границы, следовательно, для достижения максимальной прибыли в начале первого года планового периода оборудование надо сохранить. В течение первого года оборудование постареет на год. Таким образом, за пять лет до конца планового периода будем иметь оборудование возраста пяти лет. Из таблицы возьмем 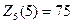. Эта клетка справа от границы, следовательно, во втором году планового периода меняем оборудование, и по окончании этого года за четыре года до конца планового периода будем иметь оборудование возраста один год и т.д. Получаем оптимальную политику управлений:

Итак, заменить оборудование необходимо только на втором году планового периода с тем, чтобы получить максимальную прибыль в размере 75 усл. ед.

Замечание 11.2. По решению для шестилетнего планового периода можно получить решение по оптимальной политике замен на каждом плановом периоде длительностью, не превосходящей шести лет.

Например, для N = 3: 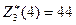и

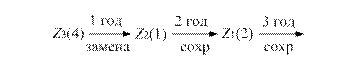
Замечание 11.3. Задачу можно усложнить, например, допуская замену не новым оборудованием, а уже проработавшим некоторое время. При этом возможны три управления: сохранение старого, покупка нового, покупка не нового оборудования.

Педагогический комментарий. Данное лекционное занятие закладывает основы для формирования следующих профессиональных умений студентов-экономистов: умение выявлять проблемы экономического характера при анализе конкретных ситуаций, предлагать способы их решения и оценивать ожидаемые результаты; умение разрабатывать и обосновывать варианты эффективных многошаговых производственно-технологических решений; умение ставить цель и формулировать задачи, связанные с профессиональной деятельностью, умение использовать для их решения методы изученных дисциплин; умение логически мыслить; умение совершенствовать составление оперативно-производственного плана с использованием инструментария математического программирования; умение эффективно управлять экономическими процессами и регулировать использование комплекса имеющихся ресурсов; умение осуществлять выбор объектов финансовых инвестиций; умение рассчитывать календарно-плановые нормативы.

Тема 12. Программирование на сетях

План лекции:

1. Основные понятия теории графов (ТГ)

2. Экстремальное дерево графа

3. Матричные способы задания графов. Упорядочение элементов

орграфа

4. Потоки на сетях. Постановка задачи о максимальном потоке

5. Разрез на сети. Теорема Форда-Фалкерсона. Алгоритм решения задачи

о максимальном потоке

Исторически теория графов, как самостоятельное научное направление возникла из задачи о семи кенигсбергских мостах, соединяющих берега и два острова на реке Преголи (рис. 12.1).

Рис. 12.1

Можно ли пройти по всем семи мостам, не проходя ни по одному из них дважды?

Граф для задачи выглядит следующим образом (рис. 12.2):

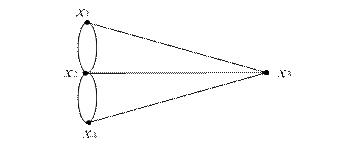
Рис. 12.2

Здесь: 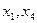– берега реки; 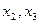– острова; линии, соединяющие точки – мосты.

Отрицательное решение этой задачи в 1736г. получено Эйлером. Со временем, результаты теории графов стали находить все более широкое применение, в том числе для решения экономических задач.

Определение 12.1. Теория графов – это раздел математики, основной особенностью которого является геометрический подход к изучению объектов.

Основным объектом теории графов является граф, который определяется заданием двух конечных дискретных множеств:

1) множество вершин ;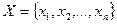

2) множество линий связи между ними .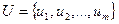

Линии связи 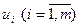называются ребрами, если не указана их ориентация; если же задано направление связи, то - дугами.

Граф, состоящий из дуг, называется ориентированным графом (орграфом), а образованный ребрами – неориентированным.

Например, 1) ориентированный граф (рис. 12.3)

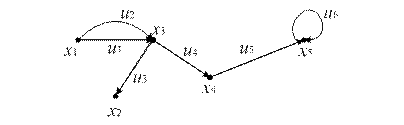
Рис. 12.3

2) неориентированный граф (рис 12.4)

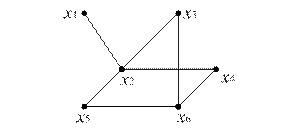
Рис. 12.4

Вершины 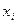и 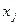, связанные дугой/ребром 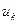, называются концевыми вершинами этой дуги/ребра. Если концевые вершины совпадают, то дугу/ребро называют петлей. Дуги/ребра с одинаковыми концевыми вершинами называются параллельными. Граф без петель и параллельных линий связи называется простым. Концевые вершины одной дуги/ребра или дуги с общей вершиной называются смежными. Простой граф, в котором каждая пара вершин смежна называется полным. Ребро/дугу называют инцидентным вершине, если оно соединено с ней.

Вывод: смежность – это отношение связности между однородными элементами (вершинами или дугами/ребрами), а инцидентность – между разнородными.

Вершина, не имеющая отношений смежности, называется изолированной. Графы с одинаковым отношением инцидентности, называются изоморфными и отличаются друг от друга только геометрической конфигурацией.

Примеры. На рисунке 12.5 представлены изоморфные графы:

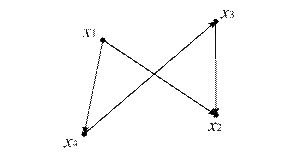
Рис. 12.5.а

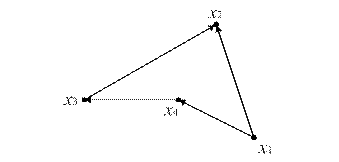
Рис. 12.5.б

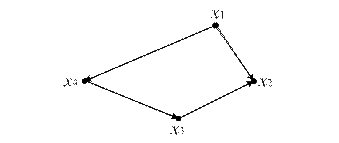
Рис. 12.5.в

Степенью P (x_i) вершины x_i называется число дуг/ребер графа, инцидентных данной вершине.

В орграфе без петель различают полустепени захода P⁺ (x_i) вершины x_i – количество дуг, входящих в x_i, и полустепени исхода P^– (x_i) – количество дуг, исходящих из вершины x_i. Понятно, что P⁺ (x_i)+P^– (x_i) =P (x_i).

В различных приложениях теории графов дугам/ребрам графов, моделирующим реальные процессы, ставят в соответствие числовые характеристики: (длина пути, время выполнения работы, пропускная способность), называемые весом дуг/ребер. В таких случаях граф называют взвешенным.

Путем в орграфе называется последовательность дуг, в которой конец любой предыдущей дуги совпадает с началом следующей. Путь, проходящий через все вершины, и притом только по одному разу, называют гамильтоновым. Путь, содержащий все дуги графа, и притом только по одному разу, называют эйлеровым. Конечный путь, у которого начальная вершина совпадает с конечной, называют контуром. Контур, проходящий через каждую вершину графа только по одному разу (за исключением начальной и конечной вершин), называют гамильтоновым.

В неориентированном графе путь называют цепью, контур – циклом. Орграф/неориентированный граф называют связным, если каждые две его вершины можно соединить путем/цепью. Орграф называют сильно связным, если между любыми двумя его вершинами существует хотя бы один путь.

Пример. а) Сильно связный граф (рис. 12.6.а)

Рис. 12.6.а

б) Несвязный граф (рис. 12.6.б)

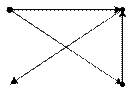
Рис. 12.6.б

Примерами графов могут служить схемы железных или шоссейных дорог, схемы связи поставщиков и потребителей, структурные формулы молекул и т.д.

Дата добавления: 2014-12-07