Задачи для контрольных работ

Ряды.

Выражение 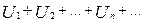называется рядом, а 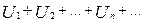,- членами ряда. Ряд записывается так: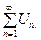

Сумму n первых его членов обозначим 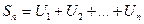и назовём n-ой частичной суммой ряда.

Если при n 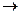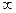существует предел последовательности частичных сумм членов данного ряда 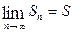,то ряд называется сходящимся, а число 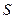-его суммой.

Пример.

Бесконечная геометрическая прогрессия представляет ряд, который сходится при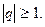

Св-ва сходящихся рядов.

1. Если ряд сходится и имеет сумму 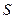, то ряд, образованный из произведений вчех членов данного ряда на одно и тоже число 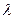тоже сходится и имеет сумму .
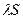2. Если сходятся ряды 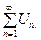и 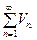, то ряд 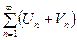тоже сходится.

Необходимый признак сходимости ряда.

Если ряд сходится, то общий член стремится к нулю при неограниченном возрастании его номера.

Достаточный признак сходимости ряда.

Если 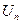не стремится к нулю, то ряд не может быть сходящимся.

Следует помнить, что стремление n-го члена ряда к нулю не является достаточным для сходимости ряда.

Пример.

Рассмотрим ряд 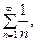который называется гармоническим. Здесь 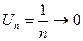, но ряд является расходящимся.

Достаточные признаки сходимости рядов.

Признаки сравнения:

1. Пусть даны 2 ряда с положительными членами и 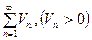и пусть каждый член ряда 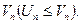Тогда оба ряда сходятся и расходятся одновременно.
2. Если предел отношения 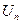к 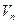существует и не равен нулю 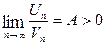, то ряды или оба сходятся или оба расходятся.

Признак Д”Aламбера:

Пусть дан ряд с положительными членами .

Если при n 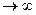существует предел отношения последнего члена к предыдущему, равным p:

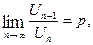то при p<1 ряд сходится. При p>1 ряд расходится. При p=1 ряд может быть как сходящимся, так и расходящимся.

Интегральный признак Коши.

Пусть дан ряд , члены которого являются значениями непрерывной функции 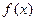при целых значениях аргумента x: 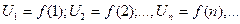и пусть 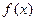монотонно убывает в интервале 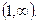Тогда ряд сходится, если сходится несобственный интеграл 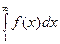и расходится, если этот интеграл расходится.

Знакочередующиеся ряды.

В таких рядах члены попеременно имеют то положительный, то отрицательный знак.

Теорема Лейбница.

Если в знакочередующемся ряде абсолютные величины членов ряда убывают, т.е. 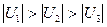и общий член 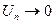, то ряд сходится.

Абсолютная сходимость.

Если ряд, составленный из абсолютных величин членов данного ряда, сходится, то сходится и данный ряд.

Пример.

Ряд 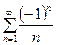условно сходящийся, т.к. по теореме Лейбница он сходится, но для него не выполняется признак абсолютной сходимости.

Радиусом сходимости степенного ряда 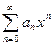называется число R такое, что при 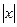< R сходится, а при 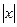> R расходится.

Интервалом сходимости ряда называется интервал (-R;R) где R – радиус сходимости

Найдем радиус сходимости ряда 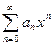через его коэффициенты. По признаку Д`Аламбера для ряда 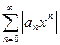при a ≠0 существует 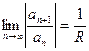, тогда

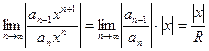
Следовательно: ряд сходится при 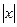< R, ряд расходится при 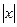> R, т.е. R радиус сходимости данного ряда. Тогда следует, что радиус сходимости ряда 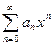определяется формулой 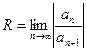, если этот предел существует.

Например:

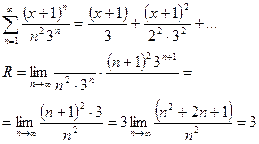
Следовательно, ряд абсолютно сходится при .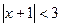

При x=2 ряд имеет вид 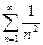и следовательно сходится.

При x= - 4 ряд 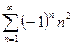сходится, по признаку Лейбница, т.е. интервалом сходимости ряда является отрезок .

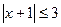Теория вероятности.

Вероятностью события А называют отношение числа благоприятных для А исходов испытания к общему числу исходов. Если обозначить m – число благоприятных для А исходов, а n – число всевозможных, то

Р(А) =

(классическое определение вероятности).

Свойства вероятности:

1⁰. Р(W) = 1.

2⁰. Вероятность невозможного события равна 0, а достоверного события равна 1. Следовательно, 0 £ Р(А) £ 1.

3⁰. Р(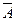) = 1 – Р(А).

Замечание. Вероятности противоположных событий удобнее обозначать буквами p и q: p=P(A), q=P().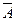

Теорема 1 (сложения). Если события А и В несовместны, то

Р(А+В) = Р(А) + Р(В)

Теорема 2. Сумма вероятностей событий А₁, А₂, …, А_n, образующих полную группу, равна 1, т.е. Р(А₁)+Р(А₂)+…+Р(А_n)=1.

Событие А называется независимым от события В, если появление события А не зависит от появления события В. В противном случае события называются зависимыми.

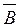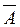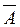Замечание. Если события А и В независимы, то независимы и события А и ; и В; и .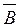

Условной вероятностью Р(В/А) называется вероятность события В, вычисленная при условии, что событие А уже произошло.

Теорема 3 (умножения). Вероятность совместного появления двух событий А и В равна

Р(АВ) = Р(А)×Р(А/В)

(причем неважно, которое из событий считать первым, а которое – вторым).

Если события А и В независимы, то теорема умножения примет вид:

Р(АВ) = Р(А)×Р(В)

Аналогично теорема умножения распространяется на случай нескольких событий:

для зависимых: Р(А₁А₂×××А_n)=Р(А₁)Р(А₂/A₁)P(A₃/A₁A₂)×××Р(А_n/A₁A₂×××A_n-1),

для независимых: Р(А₁А₂×××А_n)=Р(А₁)Р(А₂)×××Р(А_n)

Теорема 4. Пусть событие А может произойти при условии появления одного из попарно несовместных событий Н₁, Н₂, …Н_n, которые образуют полную группу, причем известны Р(Н₁), P(H₂), …, P(H_n) и Р(А/H₁), P(A/H₂), …, P(A/H_n), тогда вероятность события А равна

Р(А) = Р(Н₁)Р(А/H₁) + P(H₂)P(A/H₂) + … + P(H_n)P(A/H_n)

Эта формула называется формулой полной вероятности.

Теорема 5. Пусть событие А может произойти при условии появления одного из попарно несовместных событий Н₁, Н₂, …Н_n, которые образуют полную группу, и пусть известно, что в результате испытания событие А произошло, тогда условная вероятность i -той гипотезы равна

Р(А/H _i) =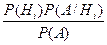

Эта формула называется формулой Байеса.

Если производится n независимых испытаний, в каждом из которых вероятность появления события А одна и та же и равна р (0<p<1), то вероятность того, что событие А появится в этих n испытаниях ровно k раз можно вычислить по формуле Бернулли:

Р_n (k)=С

где q = 1 – p.

Например. Вероятность выиграть по лотерейному билету равна 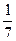. Найти вероятность выиграть по двум билетам из пяти.

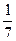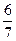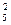
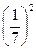
Решение: по условию р = , значит q = ; n = 5, k = 2. Тогда по формуле Бернулли получаем P₅(2)=C 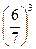= =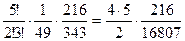0,1285.

Ответ: 0,1285.

Задания на контрольные работы.

Дата добавления: 2014-12-27