Пример 2. Одновременно, обоим неравенствам удовлетворяют точки нижней огибающей

Пример 1.

Решить игру:

Рис. 6

Одновременно, обоим неравенствам удовлетворяют точки нижней огибающей. Какое же значение р выбрать игроку А?

Разумеется, то, при котором нижняя огибающая достигнет максимума.

Решаем систему:

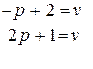
р = 1/3, 1-p = 2/3, v=5/3

Вывод: если игрок А с вероятностью 1/3 будет выбирать 1 стратегию и с вероятностью 2/3 – 2 стратегию, то при достаточно большом количестве игр с данной платежной матрицей, гарантированный средний выигрыш составит 5/3.

Другая интерпретация: чередовать стратегии в пропорции 1:2.

Чтобы найти оптимальную стратегию игрока В, воспользуемся первой строкой матрицы:

q + 3 (1-q) = v → q = 2/3, 1-q = 1/3

Фирма планирует выпуск двух моделей айфонов (игрок А).

Игрок В - спрос на продукцию. Аналитики составили платежную матрицу:

Найти оптимальную стратегию игрока А.

(почему не интересует игрок В?)

Следуем теореме Неймана.

а)находим нижнюю и верхнюю цены игры

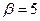
→седловой точки нет.

б) пусть (p,1- p) смешанная стратегия игрока А, (q ₁, q ₂, q ₃) смешанная стратегия игрока В.

Следуя теореме Неймана имеем:

2 p+ 7(1 -p) ≥ν→- 5 p+ 7 ≥ν (1)

3 p +5(1- p)) ≥ν→- 2 p +5 ≥ν (2)

11 p +2(1- p)) ≥ν→ 9 p +2 ≥ν (3)

в) графическая иллюстрация неравенств

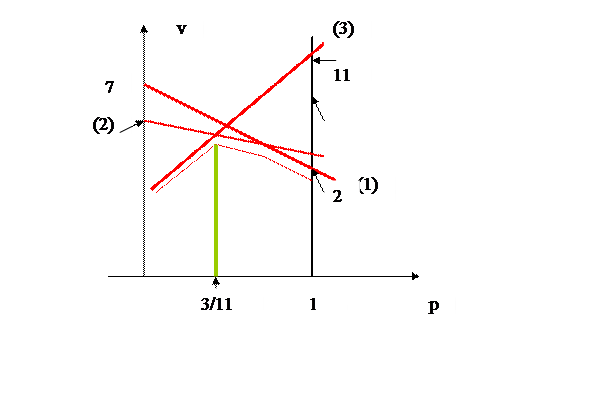
Рис. 7

Одновременно, обоим неравенствам удовлетворяют точки нижней огибающей. Какое же значение р выбрать игроку А?

Разумеется то, при котором нижняя огибающая достигнет максимума.

Решаем систему:

-2 p+ 5=ν

9 p+ 2=ν

р = 3/11, 1-p = 8/11, v = 49/11

Вывод: следует порекомендовать выпускать айфоны обеих моделей в отношении 3:8.

Чтобы найти оптимальную стратегию игрока В, заметим, что в образовании цены игры участвовали только 2-я и 3-я стратегии игрока В: 3q₂ + 11 (1-q₂) = 49/11.

q₂ = 9/11, q₃ =2/11, q₁=0.

14. Решение игры с нулевой суммой сведением к задаче линейного программирования

Покажем, как игру двух лиц с нулевой суммой можно представить задачей линейного программирования и решить, например, симплекс-методом.

Пример 1:

Решить игру, заданную платежной матрицей

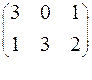α= 1, β= 2 → игра без седловой точки.

Пусть (р₁, р₂) – смешанная стратегия игрока А, (q₁, q₂, q₃) – смешанная стратегия игрока В.

Напомним, что суммы вероятностей равны 1.

Воспользуемся теоремой Неймана из раздела 12.

Для игрока А:

3р₁ + р₂ ≥ v

3р₂ ≥ v

р₁ + 2р₂ ≥ v

F = v → max

Преобразуем ограничения, разделив все члены неравенств на v (обозначим y₁ = р₁/v, y₂ = р₂/v, заметим, что v = 1/(y₁ + y₂)).

Итак, задача принимает вид:

3y₁ + y₂ ≥ 1

3y₂ ≥ 1

y₁ + 2y₂ ≥ 1

G = y₁ + y₂ → min (1)

Для игрока B:

3q₁ + q₃ ≤ v

q₁ + 3q₂ +2q₃ ≤ v

F = v → min

Преобразуем ограничения, разделив все члены неравенств на v (обозначим х₁ = q₁/v, х₂ = q₂/v, x₃= q₃/v, заметим, что

v= 1/(x₁ + x₂+x₃)).

Итак, задача принимает вид:

3x₁ + x₃ ≤ 1

x₁ + 3x₂ +2x₃ ≤ 1

f = x₁+x₂+x₃ → max (2)

Согласно моделям раздела 6 получена пара двойственных задач (1) и (2). Напомним, что, решив одну из них, например, симплекс-методом, мы автоматически найдем решение другой.

Итак, решаем задачу (2):

3x₁ + x₃ +х₄ = 1

x₁ + 3x₂ +2x₃ + х₅ = 1

F = x₁+x₂+x₃ → max

Базисн. перем.	х1	х2	х3	х4	х5	вi	Оцен. отн.
х4
х5			2				1/2
Оцен. строка	-1	-1	-1

Базисн. перем.	х1	х2	х3	х4	х5	вi	Оцен. отн.
х4	5/2	-3/2			-1/2	1/2	1/5
х3	1/2	3/2			1/2	1/2
Оцен. строка	-1/2	1/2			1/2	1/2

Базисн. перем.	х1	х2	х3	х4	х5	вi	Оцен. отн.
х1	1	-3/5		2/5	-1/5	1/5	1/5
х3		9/5		-1/5	3/5	2/5
Оцен. строка		1/5		1/5	2/5	3/5

Получено оптимальное решение:

х₁ = 1/5, х₂ =0, х₃= 2/5

v = 1/(x₁ + x₂ + x₃) = 5/3

q₁ = 1/3, q₂ = 0, q₃ = 2/3

Вывод: чтобы обеспечить гарантированный средний проигрыш 5/3 игроку В нужно с вероятностью 1/3 выбрать первую стратегию и с вероятностью 2/3 – третью стратегию

(или так- чередовать стратегии 1 и 3 в соотношении 1:2).

Чтобы найти оптимальную стратегию игрока А вспомним раздел 6: (в оценочной строке последней таблицы находим абсолютные значения балансовых переменных х₄, х₅)

у₁ = 1/5, у₂= 2/5

р₁ = (1/5)*(5/3)=1/3, р₂ = 2/3.

Пример 2: (военная игра НАТО)

На маневрах флота в средиземном море сторона В может послать подводную лодку в один из регионов моря: 1 или 2. Другая сторона А имеет 3 противолодочных корабля и должна обнаружить и уничтожить подводную лодку.

Вероятность корабля потопить лодку в регионе 1 равна 0,6, а в регионе 2 - 0,4. Командованию флота нужно разработать стратегию распределения кораблей по регионам.

Данную конфликтную ситуацию рассмотрим как игру двух игроков А и В.

У игрока В две стратегии - послать лодку в регион 1 и в регион 2. У игрока А четыре стратегии (0,3), (1,2), (2,1) и (3,0).

Например, (2,1) означает посылку двух кораблей в 1 регион и одного - во 2 регион, и т.п.

Выигрыш игрока А – вероятность уничтожения лодки.

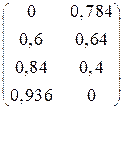α=0,6, β=0,784

Поясним составление платежной матрицы.

(0,3)- посылка 0 кораблей в 1 регион и 3 кораблей во второй.

При этом в первом регионе имеется лодка - ясно, что вероятность ее уничтожения 0.

Пусть игрок В направил лодку во 2 регион:

вероятность того, что хотя бы один из 3-х кораблей уничтожит лодку: р = 1 – (1- 0,4)³ =0,784.

(2,1)- посылка 2 кораблей в 1 регион и одного корабля во 2 регион. Пусть игрок В направил лодку в 1 регион:

Р = 1- (1-0,6)² = 0,64 и т.д. (просчитать вероятности самостоятельно).

Рассуждая, так же как и в первом примере:

Для игрока А:

0,6у₂ + 0,84у₃ + 0,936 у₄ ≥ 1

0,784у₁ + 0,64у₂ + 0,4 у₃ ≥ 1

F = у₁ + у₂ + у₃ + у₄ → min (1)

Для игрока В:

0,784х₂ ≤ 1

0,6х₁ + 0,64х₂ ≤ 1

0,84х₁ + 0,4х₂ ≤ 1

0,936х₁ ≤ 1

G= x₁ + x₂ → max (2)

Решим задачу (1) в EXCEL. (файл игра).

у₁ =0, у₂= 1,48, у₃=0,13, у₄=0, v= 1/(у₁+у₂ + у₃ + у₄)= 1/1,61 = 0,62

р₁=0, р₂ =1,48*0,62= 0,92, р₃=0,13*0,62= 0,08, р₄ =0

Итак, оптимальная стратегия игрока А – послать 1 корабль в 1-й регион с вероятностью 0,92 и 2- в 1 регион с вероятностью 0,08. Не следует посылать 3 корабля во 2 -й регион и 3 корабля в 1 регион!

Пример 3.

Найти решение игры, заданной платежной матрицей:

Решаем игру сведением к двойственным задачам.

Для игрока А:

4у₁ + 3у₂ + 2 у₃ ≥ 1

-2у₁ + 5у₂ + у₃ ≥ 1

2у₁ + у₂ + 5у₃ ≥ 1

G = у₁ + у₂ + у₃ → min (1)

Для игрока В:

4х₁ – 2х₂ + 2х₃ ≤ 1

3х₁ + 5х₂ + х₃ ≤ 1

2х₁ + х₂ + 5х₃ ≤ 1

F = х₁ + х₂ + х₃ → max (2)

Решим задачу (1) в EXCEL:

у₁ = 0,03 у₂ = 0,19 у₃= 0,15

v= 1/ (0,03 + 0,19 + 0,15)= 2,7

р₁ = 0,03*2,7=0,081

р₂ = 0,19*2,7 =0,513

р₃ = 0,15*2,7 =0,405

Наиболее обещающей для игрока А является 2-я стратегия.

Решим задачу (2) в EXCEL:

х₁ = 0,22 х₂ = 0,05 х₃= 0,1

v= 1/ (0,22 + 0,05 + 0,1)= 2,7

q₁ = 0,22*2,7=0,594

q₂ = 0,05*2,7 =0,135

q₃ = 0,1*2,7 =0,27

Дата добавления: 2014-12-27