Устойчивость выборочных средних

Оценка генеральной средней по выборочной средней.

Сложение дисперсий.

Теорема: Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий:

= +

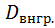Доказательство: Для упрощения доказательства предположим, что вся совокупность значений количественного признака Х разбита на две следующие группы:

группа №1 №2

значение признака , ,

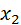
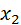
частота , ,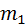

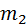
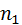объем группы = =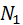

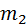
групповая средняя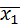

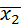
групповая дисперсия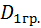

Объем всей совокупности

(для удобства вместо будем писать Σ)

(1)

Преобразуем первое слагаемое числителя, вычитая и прибавляя :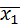

=

.

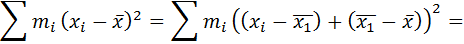
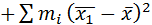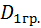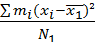= , тогда

Т.к. то первое слагаемое принимает вид:

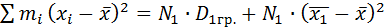(2)

Аналогично второе слагаемое принимает вид:

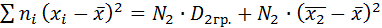(3)

Представим (2) и (3) в формулу (1):

+

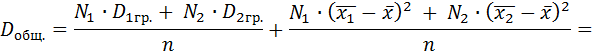
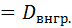Что и требовалось доказать.

6.Основные точечные оценки.

Пусть из генеральной совокупности в результате n независимых наблюдений над количественным признаком Х извлечена повторная выборка объема n со значениями признака …, . Не уменьшая общности рассуждений, будем считать значения признака различными.

Пусть генеральная средняя 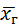неизвестна и требуется оценить ее по данным выборки.

В качестве оценки 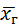принимают .

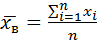Убедимся, что несмещенная оценка, т.е. математическое ожидание этой оценки равно .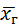

Будем рассматривать , как случайную величину, и 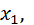…, как независимые, одинаково распределенные случайные величины 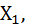…, 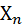. Следовательно, эти величины имеют одинаковые математические ожидания .

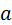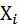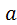Известно, что М () = M( ) = , i= 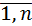. Следовательно,

M( 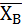) = M() = 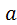. (1)

Т.к. каждая из величин 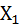, …, 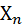имеет то же распределение, что и генеральная совокупность (которую мы тоже рассматриваем как случайную величину), то числовые характеристики одинаковые, следовательно, математическое ожидание 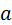каждой из величин равно математическому ожиданию признака Х генеральной совокупности, т.е.

М(Х) = .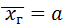

Заменив в формуле (1) 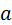на 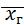, получим:

M( )= .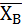

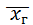Т. о., 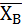– несмещенная оценка генеральной средней.

Легко показать, что выборочная средняя является и состоятельной оценкой генеральной средней.

Действительно, допуская, что случайные величины 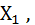…, 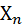имеют ограниченные дисперсии, применяем к этим величинам теорему Чебышёва (частный случай). Т.е. при увеличении n среднее арифметическое рассматриваемых величин, т.е. 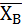, стремится по вероятности к математическому ожиданию 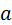каждой из величин, или, что тоже самое, к генеральной средней 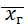(т.к. = ).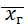

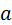Свойство устойчивости выборочных средних: Если по нескольким выборкам достаточно большого объема из одной и той же генеральной совокупности будут найдены выборочные средние, то они будут приближенно равны между собой.

Заметим, что чем больше объем выборки, тем меньше выборочная средняя отличается от генеральной средней.

Мы предполагали выборку повторной. Но полученные выводы применимы и для бесповторной выборки, если ее объем значительно меньше объема генеральной совокупности.

Дата добавления: 2014-12-27