Отношения

Свойства выборочного корреляционного

Выборочное корреляционное отношение 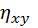обладает теми же свойствами, что и . Поэтому рассмотрим , которое далее, для упрощения записи, будем обозначать 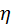и, для простоты речи, называть «корреляционным отношением».

Свойство 1: Корреляционное отношение удовлетворяет неравенству 0 .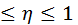

Доказательство: 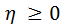, т.к. .

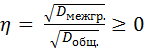Докажем, что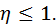

Разделим обе части этого равенства на :

1 = +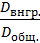

1= +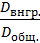

Т.к. оба слагаемых неотрицательны и их сумма равна 1, то каждое из них не превышает 1, т.е., в частности, η² ≤ 1.

Итак, 0 ≤ η ≤ 1.

Свойство 2: Если η = 0, то признак Y с признаком X корреляционной зависимостью не связан.

Доказательство: η = 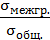_. = 0. А это означает, что σ_межгр= 0, следовательно, D _межгр = 0.

Межгрупповая дисперсия есть дисперсия условных (групповых) средних 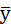_x относительно общей средней .

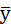Тот факт, что D _межгр = 0 означает, что при всех значениях X условные средние сохраняют постоянное значение, равное общей средней. Т.е. при η = 0 условная средняя не является функцией от X, а значит, признак Y не связан корреляционной зависимостью с признаком X.

Заметим, что можно доказать и обратное: если признак Y не связан с признаком X корреляционной зависимостью, то η = 0.

Свойство 3: Если η =1, то признак Y связан с признаком X функциональной зависимостью.

Доказательство: По условию, η = 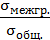= 1. Это означает, что σ_общ.= σ_межгр , возводя обе части этого равенства в квадрат, получим:

D _общ. = D _межгр. (1)

Т.к. D _общ. = D _внгр.+ D _межгр., то, в силу формулы (1), имеем:

D _внгр.= 0 (2)

Поскольку внутригрупповая дисперсия есть среднее арифметическое групповых дисперсий (взвешенное по объемам групп), то из формулы (2) следует, что дисперсия каждой группы (т.е. значений Y, соответствующих определенному значению X) равна нулю. А это означает, что в группе содержатся разные значения Y, т.е. каждому значению X соответствует одно значение Y. Следовательно, при η = 1 признак Y связан с признаком X функциональной зависимостью.

Заметим, что можно доказать и обратное: если признаком Y связан с признаком X функциональной зависимостью, то η =1.

Приведем еще два свойства, опустив доказательства.

Свойство 4: η ≥ | |.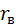

Свойство 5: Если η = | 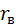|, то имеет место точная линейная корреляционная зависимость.

Другими словами, если η = | 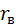|, то точки (x₁, y₁), (x₂, y₂),..., (x_n, y_n) лежат на прямой линии регрессии, найденной методом наименьших квадратов.

При определении корреляционного отношения форма связи не принималась во внимание, отсюда вытекает его достоинство и недостаток.

Достоинство: η служит мерой тесноты связи любой формы, в том числе и линейной.

Недостаток: η не позволяет судить о том, насколько близко расположены точки, найденные по данным наблюдений, к кривой определенного вида, например к параболе, гиперболе и других.

Дата добавления: 2014-12-27