
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дисперсионного анализа
|
|
|
|
Сравнение нескольких средних методом
Поставим задачу: Проверить при заданном уровне значимости нулевую гипотезу о равенстве нескольких  средних нормальных совокупностей с неизвестными, но одинаковыми дисперсиями.
средних нормальных совокупностей с неизвестными, но одинаковыми дисперсиями.
Покажем, что решение этой задачи сводится к сравнению факторной и остаточной дисперсий по критерию Фишера-Снедекора.
Пусть нулевая гипотеза о равенстве средних (далее будем называть их групповыми) справедлива. В этом случае факторная и остаточная дисперсии являются несмещенными оценками неизвестной генеральной дисперсии, и, следовательно, различаются незначительно. Если сравнить эти оценки по критерию F, то, очевидно, критерий укажет, что нулевую гипотезу о равенстве факторной и остаточной дисперсий следует принять.
Таким образом, если гипотеза о равенстве групповых средних правильна, то верна и гипотеза о равенстве факторной и остаточной дисперсий.
Пусть нулевая гипотеза о равенстве групповых средних ложна. В этом случае с возрастанием расхождения между групповыми средними увеличивается факторная дисперсия, а вместе с ней и величина 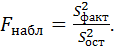
В итоге 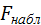 окажется больше
окажется больше 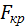 и, следовательно, гипотеза о равенстве дисперсий будет отвергнута.
и, следовательно, гипотеза о равенстве дисперсий будет отвергнута.
Таким образом,если гипотеза о равенстве групповых средних ложна, то ложна и гипотеза о равенстве факторной и остаточной дисперсий.
Легко доказать от противного справедливость обратных утверждений: из правильности (ложности) гипотезы о дисперсиях следует правильность (ложность) гипотезы о средних.
Вывод: Для того чтобы проверить нулевую гипотезу о равенстве групповых средних нормальных совокупностей с одинаковыми дисперсиями, достаточно проверить по критерию F нулевую гипотезу о равенстве факторной и остаточной дисперсий.
|
|
|
В этом и состоит метод дисперсионного анализа.
Заметим, что если 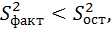 то справедлива гипотеза о равенстве групповых средних а, значит, нет надобности прибегать к критерию
то справедлива гипотеза о равенстве групповых средних а, значит, нет надобности прибегать к критерию 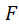 .
.
Если нет уверенности в справедливости предположения о равенстве дисперсий рассматриваемых р совокупностей, то это предположение следует проверить предварительно, по другому критерию.
Пример: Произведено по четыре испытания на каждом их трех уровней. Результаты приведены в таблице. Методом дисперсионного анализа при уровне значимости 0,05 проверить нулевую гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
| i | F1 | F2 | F3 |
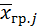
|
Решение: Составим расчетную таблицу. Пользуясь таблицей, и, учитывая что число уровней фактора р = 3, число испытаний на каждом уровне q = 4, найдем общую и факторную суммы квадратов отклонений.
| i | F1 | F2 | F3 | |||
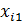
| 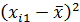
| 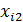
| 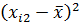
| 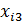
| 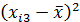
| |
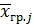
| - | - | 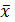 = 52 = 52
| |||
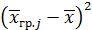
| - | - |
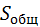 = 226,
= 226,
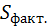 = 4
= 4  (4 + 9 + 25) = 152,
(4 + 9 + 25) = 152,
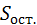 =266 – 152 = 144,
=266 – 152 = 144,
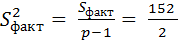 = 76,
= 76,

Теперь сравним факторную и остаточную дисперсии по критерию F:
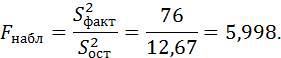
Учитывая, что число степеней свободы числителя 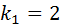 , а число степеней свободы знаменателя
, а число степеней свободы знаменателя 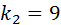 и уровень значимости α = 0,05, по таблице находим критическую точку:
и уровень значимости α = 0,05, по таблице находим критическую точку:
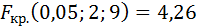
Так как 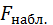 >
> 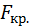 гипотезу о равенстве групповых средних отвергаем. Другими словами, групповые средние «в целом» различаются значимо. Если требуется сравнить средние попарно, то следует воспользоваться критерием Стьюдента.
гипотезу о равенстве групповых средних отвергаем. Другими словами, групповые средние «в целом» различаются значимо. Если требуется сравнить средние попарно, то следует воспользоваться критерием Стьюдента.
13.2.5.Неодинаковое число испытаний на различных уровнях фактора. 
Пусть произведено 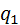 испытаний на уровне
испытаний на уровне 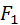 ,
, 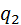 испытаний – на уровне
испытаний – на уровне 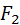 , …, qp испытаний – на уровне
, …, qp испытаний – на уровне 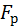 .
.
В этом случае общую сумму квадратов отклонений находят по формуле:
|
|
|
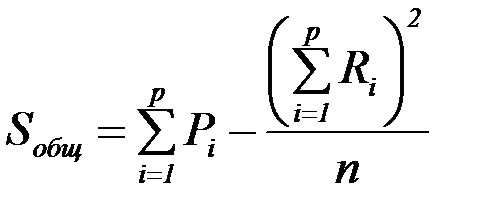 ,
,
где 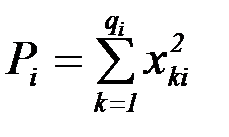 – сумма квадратов наблюдавшихся значений признака на уровне
– сумма квадратов наблюдавшихся значений признака на уровне 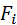 ;
; 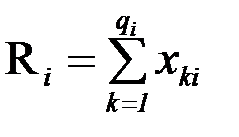 – сумма наблюдавшихся значений признака на уровне
– сумма наблюдавшихся значений признака на уровне 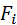 ;
; 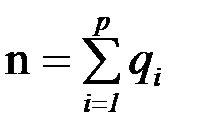 – общее число испытаний (объем выборки).
– общее число испытаний (объем выборки).
Факторную сумму квадратов отклонений находят по формуле:
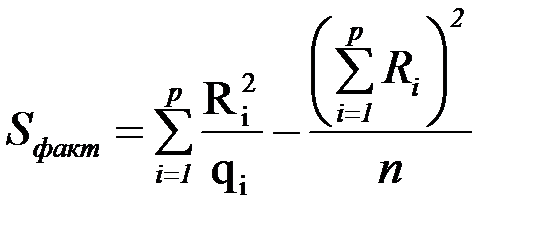 .
.
Остальные вычисления производят, как и в случае одинакового числа испытаний: 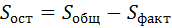
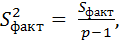
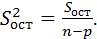
Пример: Произведено 10 испытаний, из них 4 – на первом уровне фактора, 4 – на втором, и 2 – на третьем. Результаты приведены в таблице. Методом дисперсионного анализа при уровне значимости 0,01 проверить нулевую гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
| i | F1 | 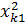
| F2 | 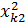
| F3 | 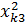
|
| - | - | |||||
| - | - | |||||
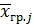
| - | - | - | |||
| Σ |
Решение:
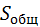 = 44942 -
= 44942 - 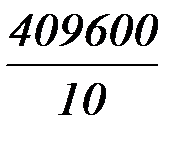 = 3982,
= 3982,
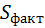 = (7056+23104+14112) -
= (7056+23104+14112) - 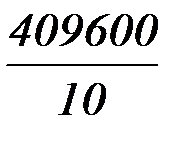 = 44272 – 40960 =3312,
= 44272 – 40960 =3312,
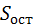 = 3982 – 3312 = 670,
= 3982 – 3312 = 670,
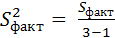 = 1656,
= 1656,
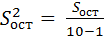 = 95,7142.
= 95,7142.
Сравним факторную и остаточную дисперсии по критерию F:
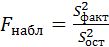 = 17,3015.
= 17,3015.
Учитывая, что число степеней свободы числителя 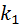 = 2, а число степеней свободы знаменателя
= 2, а число степеней свободы знаменателя 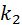 = 7, и уровень значимости
= 7, и уровень значимости 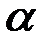 =0,01, по таблице находим критическую точку:
=0,01, по таблице находим критическую точку:
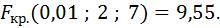
Так как 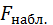 >
> 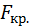 , то нулевую гипотезу о равенстве групповых средних отвергаем. Групповые средние различаются значимо.
, то нулевую гипотезу о равенстве групповых средних отвергаем. Групповые средние различаются значимо.
Заключение
Математическая подготовка экономиста имеет свои особенности, связанные со спецификой экономических задач, а также с широким разнообразием подходов к их решению. Задачи практической и теоретической экономики очень разносторонни. К ним относятся, в первую очередь, методы сбора и обработки статистической информации, а также оценка состояния и перспективы развития экономических процессов.
Неопределенность экономических процессов, значительный случайный разброс и большой объем получаемой информации обусловливают необходимость привлечения к исследованию экономических задач теории вероятностей и математической статистики.
Автор надеется, что благодаря и этой книге будущие экономисты освоят современный математический аппарат и в дальнейшем смогут успешно решать свои профессиональные задачи.
Список литературы:
|
|
|
1. ГМУРМАН В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2010.
2. ГМУРМАН В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2010.
3. ЗВЕРЕВА Е.Н.Математическая статистика. Методические указания и контрольные задания для студентов очной формы обучения. — СПбГИЭУ, 2005.
4. КОБЗАРЬ А.И. Прикладная математическая статистика. — М.: Физматлит, 2006.
5. КРАСС М.С., ЧУПРЫНОВ Б.П. Основы математики и ее приложения в экономическом образовании. – М.: Дело, 2002.
6. ЛАГУТИН М.Б. Наглядная математическая статистика. В двух томах. — М.: П-центр, 2003.
7. Общий курс высшей математики для экономистов под редакцией проф. В.И. ЕРМАКОВА – М.: ИНФРА-М, 2009.
8. Сборник задач по высшей математике для экономистов под редакцией проф. В.И. ЕРМАКОВА – М.: ИНФРА-М, 2009.
9. ЧИСТЯКОВ В.П. Курс теории вероятностей.– М.: Наука, 1987.
10. Carlin, B.P. and Louis, T.A. (2008) Bayesian Methods for Data Analysis, Third Edition. Chapman & Hall/CRC.
11. http://ru.science.wikia.com
Сведения об авторе
Светлана Евгеньевна Игнатова – кандидат экономических наук, доцент кафедры высшей математики СПбГИЭУ. Специалист в области математики, математических методов и моделей в экономике, преподавания математики в высшей школе.
Окончила Математико-механический факультет Санкт-Петербургского государственного университета по специальности «математика». Защитила кандидатскую диссертацию в 2003 году с СПбГИЭУ. Научные исследования посвящены экономико-математическому моделированию.
Автор более 20 научных и учебно-методических печатных работ.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1775; Нарушение авторских прав?; Мы поможем в написании вашей работы!