Непрерывной случайной величины

Плотность распределения вероятностей

Непрерывную случайную величину можно задать с помощью другой функции (кроме функции распределения), которую называют плотностью распределения или плотностью вероятности.

Определение: Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f(x) –первую производную от функции распределения F(x):

График плотности распределения называют кривой распределения.

Теорема: Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (а,b), равна определённому интегралу от плотности распределения, взятому в пределах от a до b:

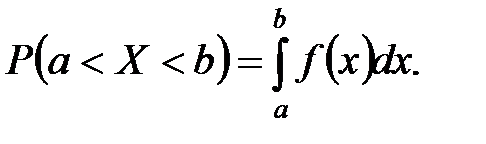
Доказательство: Воспользуемся следствием 1, вытекающим из второго свойства функции распределения вероятностей:

По формуле Ньютона-Лейбница имеем:

Так как для непрерывной случайной величины справедлива формула , то теорема доказана.

С геометрической точки зрения вероятность попадания непрерывной случайной величины в заданный интервал равна площади криволинейной трапеции, ограниченной сверху графиком плотности распределения: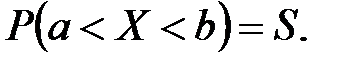

f(x)

S

a b X

Заметим, что если f(x) – четная функция, и концы интервала симметричны относительно начала координат, то получаем упрощенную формулу:

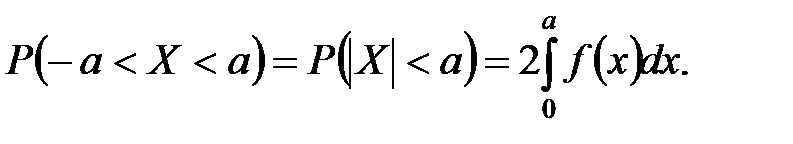
Пример: Непрерывная случайная величина задана плотностью распределения:

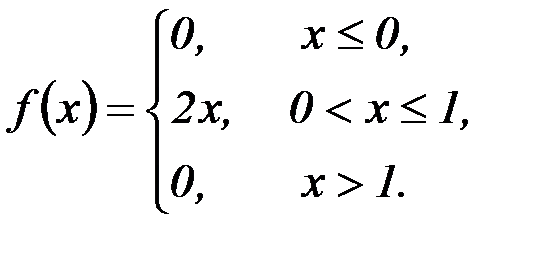
Требуется найти P(0,5< X<1).

Решение: По теореме получаем:

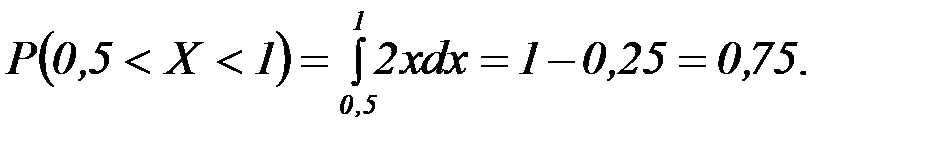
Зная плотность распределения f(x), можно найти функцию распределения F(x) по формуле:

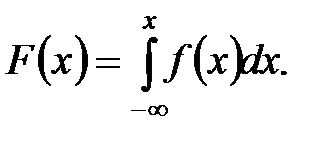
Выведем эту формулу. Для этого воспользуемся определением функции распределения:

Как известно,

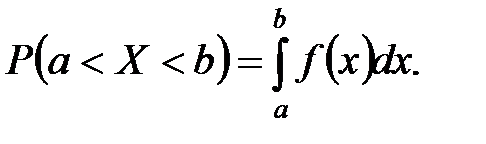
Полагая a = - , b = x, имеем:

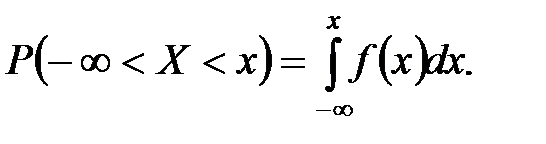
Таким образом,

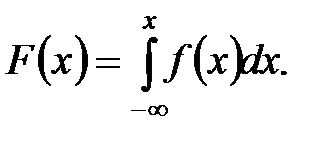
Заметим, что более корректной будет запись:

Пример: По условию предыдущего примера найдём функцию распределения F(x).

Решение: Так какплотность распределения –кусочная функция, то и функция распределения также будет кусочной функцией.

Окончательно получаем:

Рассмотрим основные свойства плотности распределения:

Свойство 1: Плотность распределения – неотрицательная функция:

f(x) 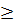0.

Доказательство: Функция распределения F(x) – неубывающая функция, следовательно, ее производная 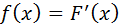– функция неотрицательная.

Свойство 2: Несобственный интеграл от плотности распределения в пределах от 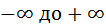равен единице:

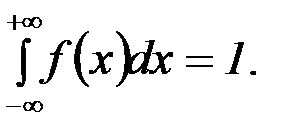
Доказательство: Несобственный интеграл

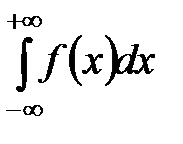
выражает вероятность события, состоящего в том, что случайная величина примет значение, принадлежащее интервалу (. Очевидно, такое событие достоверно, следовательно, его вероятность равна 1.

Геометрически это означает, что площадь криволинейной трапеции под графиком плотности распределения по бесконечному промежутку равна единице.

f(x)

S

X

S = 1.

Заметим, что плотность распределения непрерывной случайной величины называют также законом распределения этой величины.

Рассмотрим вероятностный смысл плотности распределения.

Пусть F(x) – функция распределения непрерывной случайной величины X.

По определению плотности распределения, имеем:

где l – длина интервала (x; x+ x).

По аналогии с определением физической плотности

где F(х) – закон распределения массы, можно рассматривать значение 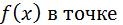х,как плотность вероятности в этой точке. Этот факт объясняет название «плотность».

Из дифференциального исчисления известно, что

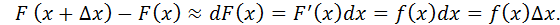
Вывод: Вероятность того, что случайная величина примет значение, принадлежащее интервалу 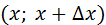, приближённо равна (с точностью до бесконечно малых высшего порядка относительно 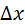) произведению плотности вероятности в точке х и длины интервала .

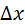С геометрической точки зрения вероятность того, что случайная величина примет значение, принадлежащее интервалу 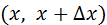, приближённо равна площади прямоугольника с основанием 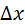и высотой

f(x) C

A B

S

x x+Δx X

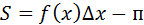лощадь прямоугольника, приближенно равная площади криволинейной трапеции. Допущенная при этом погрешность равна площади криволинейного треугольника АВС.

Дата добавления: 2014-12-27