
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дисперсия
|
|
|
|
Зная лишь математическое ожидание случайной величины, нельзя судить о том, какие возможные значения она может принимать или о том, как они рассеяны вокруг математического ожидания. Например, пусть случайные величины X и Y имеют распределения:
| X | -0,01 | 0,01 |
| P | 0,5 | 0,5 |
| Y | -100 | 100 |
| P | 0,5 | 0,5 |
Несмотря на столь большое различие между возможными значениями этих величин, они имеют одинаковые математические ожидания: M(X) = M(Y) = 0.
Нужна другая числовая характеристика – дисперсия. Но сначала дадим определение отклонения случайной величины от ее математического ожидания.
Определение: Отклонением называется разность между случайной величиной и ее математическим ожиданием:
X – M(X).
Пусть дискретная случайная величина X задана законом распределения:
| X | 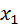
| 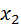
| … | 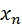
|
| P | 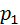
| 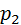
| … | 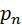
|
Напишем закон распределения отклонения. Для того, чтобы отклонение приняло значение 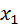 – M(X), достаточно, чтобы случайная величина приняла значение
– M(X), достаточно, чтобы случайная величина приняла значение 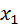 .
.
Если P(X = 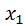 )=
)=  , тогда и P(X – M(X) =
, тогда и P(X – M(X) = 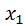 – M(X)) =
– M(X)) =
 .
.
Аналогично для остальных значений. Таким образом, получаем закон распределения:
| X – M(X) | 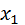 – M(X) – M(X)
| 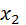 – M(X) – M(X)
| … |  – M(X) – M(X)
|
| P | 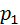
| 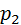
| … | 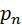
|
Теорема: Математическое ожидание отклонения равно нулю:
М(X – M(X)) = 0.
Доказательство: Пользуясь свойствами математического ожидания, и, приняв во внимание, что М(Х) – постоянная величина, имеем:
М(X – M(X)) = М(X) + М(– M(X)) = М(X) – M(X) = 0.
Это свойство объясняется тем, что одни возможные значения отклонения положительны, а другие – отрицательны. В результате их взаимного «погашения» математическое ожидание равно нулю. Поэтому целесообразно заменить отклонения их квадратами.
Определение: Дисперсией (рассеянием) случайной величины (непрерывной или дискретной) называется математическое ожидание квадрата отклонения этой случайной величины от ее математического ожидания:
|
|
|
D(X) = М(X – M(X))2.
Из данного определения следует, что дисперсия – неслучайная (постоянная) величина, и она неотрицательна.
Согласно данному определению, дисперсию дискретной случайной величиныможно вычислить по формуле:
D(X) = ( 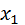 – M(X))2
– M(X))2  + (
+ ( 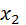 – M(X))2
– M(X))2  + … + (
+ … + (  – M(X))2
– M(X))2 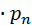 .
.
Если Х – непрерывная случайная величина, возможные значения которой принадлежат отрезку  , а плотность распределения равна f(x), то дисперсию можно вычислить по формуле:
, а плотность распределения равна f(x), то дисперсию можно вычислить по формуле:
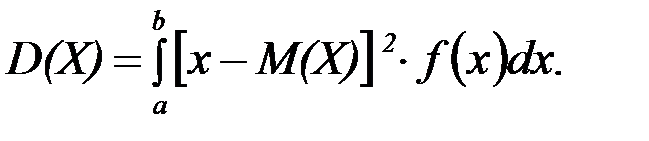
Заметим, что вместо отрезка может быть интервал или полуинтервал.
Если возможные значения Х принадлежат всей числовой оси, то дисперсию можно вычислить по формуле:

Для вычисления дисперсии часто бывает удобно пользоваться следующей теоремой.
Теорема: Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом математического ожидания этой величины:
D(X) = М(X 2) – M 2(Х).
Доказательство: М(Х) – постоянная величина, следовательно, 2М(Х) и M 2(Х) также постоянные величины. Пользуясь свойствами математического ожидания, имеем:
D(X) = М(X – M(X))2 = М(Х 2 – 2ХМ(Х) + M 2(Х)) = М(Х 2) –
– М(2ХМ(Х)) + М(M 2(Х)) = М(Х 2) – 2М(Х)М(Х) + M 2(Х) =
= М(X 2) – M 2(Х).
Согласно этой теореме и формулам для математического ожидания, запишем новые формулы для вычисления дисперсии дискретной и непрерывной случайных величин соответственно:


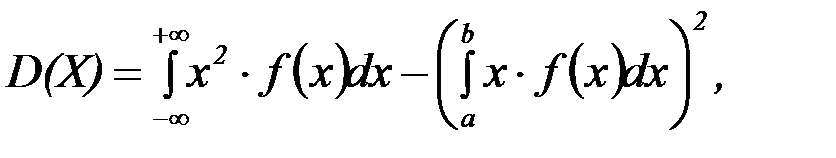
где f(x) – плотность распределения непрерывной случайной величины Х.
Пример: Дискретнаяслучайная величина X задана законом распределения:
| X | 2 | 3 | 5 |
| P | 0,1 | 0,6 | 0,3 |
Вычислим дисперсию X по теореме:
D(X) = М(X 2) – M 2(Х) = 22  0,1 + 32
0,1 + 32 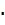 0,6 + 52
0,6 + 52 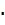 0,3 – (2
0,3 – (2 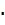 0,1 +
0,1 +
+ 3 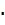 0,6 + 5
0,6 + 5 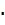 0,3)2 = 13,3 – (3,5)2 =1,05.
0,3)2 = 13,3 – (3,5)2 =1,05.
Заметим, что дисперсия - характеристика рассеяния возможных значений случайной величины вокруг ее математического ожидания.
Рассмотрим основные свойства дисперсии.
|
|
|
Свойство 1: Дисперсия постоянной величины равна нулю, т.е.
D(С) =0,
где С – постоянная величина.
Доказательство: Воспользуемся определением дисперсии и свойством математического ожидания:
D(С) = М(С – M(С))2 = М(С – С)2 = М(0) = 0.
Действительно, постоянная величина сохраняет одно и то же значение и рассеяния не имеет.
Свойство 2: Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат, т.е.
D(СХ) =С2 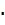 D(Х),
D(Х),
где С – постоянная величина.
Доказательство: Воспользуемся определением дисперсии и свойством математического ожидания:
D(СХ) = М(СХ – M(СХ))2 = М(СХ – СM(Х))2 =
= М(С2 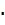 (Х – M(Х))2 ) = С2
(Х – M(Х))2 ) = С2 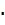 М(Х – M(Х))2 = С2
М(Х – M(Х))2 = С2 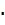 D(Х).
D(Х).
Свойство 3: Дисперсия суммы двух независимых случайных величин X и Y равна сумме дисперсий этих величин:
D(X +Y) =D(X) + D(Y).
Доказательство: По формуле для вычисления дисперсии (согласно теореме) и по свойствам математического ожидания суммы нескольких случайных величин и произведения двух независимых случайных величин имеем:
D(X + Y) = М((X + Y) 2) – M 2(X + Y) = М(X 2 + 2ХY + Y 2) –
–(M(X) + М(Y)) 2 = М(X 2) + 2М(ХY) + М(Y 2) – (M 2(X) +2М(X) 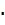
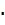 М(Y) + М 2(Y)) = М(X 2) + 2М(Х)
М(Y) + М 2(Y)) = М(X 2) + 2М(Х) 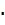 М(Y) + М(Y 2) – M 2(X) – 2М(X)
М(Y) + М(Y 2) – M 2(X) – 2М(X) 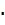
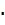 М(Y) – М 2(Y) = М(X 2) + М(Y 2) – M 2(X) – М 2(Y) = М(X 2) –
М(Y) – М 2(Y) = М(X 2) + М(Y 2) – M 2(X) – М 2(Y) = М(X 2) –
– M 2(X)+ М(Y 2) – М 2(Y) = D(X) + D(Y).
Из этого свойства вытекают два следствия.
Следствие 1: Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин.
Доказательство: Пусть X, Y, Z – взаимно независимые случайные величины. Тогда, опираясь на свойство3, имеем:
D(X + Y + Z) = D(X) + D(Y + Z)= D(X) + D(Y) + D (Z).
Для произвольного числа слагаемых доказательство проверяется методом математической индукции.
Следствие 2: Дисперсия суммы постоянной величины С и случайной величины X равна дисперсии случайной величины X:
D(С + X) = D(X).
Доказательство: Величины С и Х независимы, поэтому, по свойству 3, получаем:
D(С + X) = D(С) + D(X) = 0 +D(X) = D(X).
Свойство 4: Дисперсия разности двух независимых случайных величин X и Y равна сумме дисперсий этих величин:
D(X – Y) = D(X) + D(Y).
Доказательство: Пусть X и Y – независимые случайные величины. Тогда, опираясь на свойства 2 и 3, имеем:
D(X – Y) = D(X) + D(–Y)= D(X) + (–1)2D(Y) = D(X) + D(Y).
Теорема: Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления р и непоявления q события в одном испытании:
|
|
|
D(X) = npq.
Доказательство: Пусть Х – число появлений события А в n независимых испытаниях. Очевидно, общее число появлений события в этих испытаниях равно сумме появлений события в отдельных испытаниях:
 ,
,
где Хi – число наступлений события в i -ом испытании, i = 1, …, n.
Величины  взаимно независимы, т.к. исход каждого испытания не зависит от исходов остальных. Тогда по свойству 3 дисперсии имеем:
взаимно независимы, т.к. исход каждого испытания не зависит от исходов остальных. Тогда по свойству 3 дисперсии имеем:
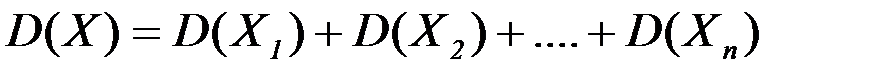 .
.
Вычислим дисперсию числа наступлений события в первом испытании:
 .
.
Из ранее изложенной теории известно, что
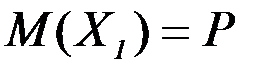 .
.
Найдем M( ). Составим закон распределения случайной величины
). Составим закон распределения случайной величины  :
:

| 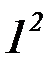
| 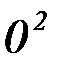
|

| p | q |

Тогда получаем:
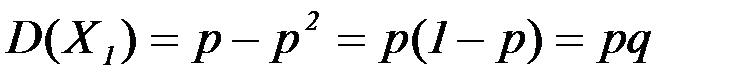 .
.
Очевидно, 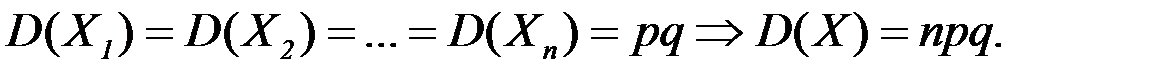
Пример: Производится 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти D(X), где Х – число появлений события в этих испытаниях.
Решение: Так как n=10, p=0,6; q=0,4, то, согласно теореме, легко вычислить дисперсию:

|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1465; Нарушение авторских прав?; Мы поможем в написании вашей работы!