Зависимые и независимые случайные величины.

Условные распределения независимых случайных величин равны их безусловным распределениям.

Теорема: Для того, чтобы случайные величины 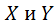были независимыми, необходимо и достаточно, чтобы функция распределения вероятностей соответствующей двумерной случайной величины 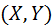была равна произведению функций распределения вероятностей ее компонент:

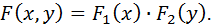
Доказательство: Сначала докажем необходимость. Пусть случайные величины независимы. Следовательно, события 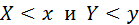также независимы. Тогда имеем:

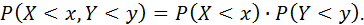
По определению функции распределения получаем:

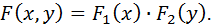
Теперь докажем достаточность. Пусть выполняется равенство:

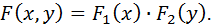
По определению функции распределения это означает, что:

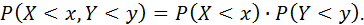
Следовательно, случайные величины независимы.

Следствие: Для того, чтобы непрерывные случайные величины 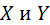были независимыми, необходимо и достаточно, чтобы плотность совместного распределения вероятностей соответствующей двумерной случайной величины 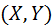была равна произведению плотностей распределения вероятностей ее компонент:

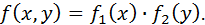
Доказательство: Сначала докажем необходимость. Пусть непрерывные случайные величины независимы. Тогда, на основании теоремы, имеем:

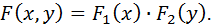
Продифференцируем это равенство по x, затем по y:

.

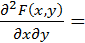
По определению плотности распределения вероятностей двумерной и одномерной случайной величины, получаем:

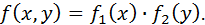
Теперь докажем достаточность. Пусть выполняется равенство:

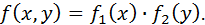
Проинтегрируем это равенство по x, затем по y:

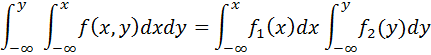
А это то же самое, что 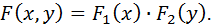На основании теоремы это и озачает, что 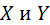– независимы.

Так как приведённые выше условия являются необходимыми и достаточными, то можно дать новые определения независимых случайных величин.

Определение: Две случайные величины 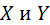называются независимыми, если функция распределения вероятностей соответствующей двумерной случайной величины 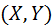равна произведению функций распределения вероятностей ее компонент.

Определение: Две непрерывные случайные величины 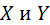называются независимыми, если плотность совместного распределения вероятностей соответствующей двумерной случайной величины 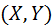равна произведению плотностей распределения вероятностей ее компонент.

Дата добавления: 2014-12-27