Теорема Блоха и наноразмерность

Пусть имеется периодический потенциал вида (рис. 2.4).

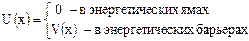(2.24)

Энергию электрона обозначим Е.

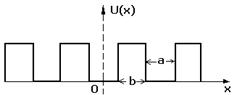
Рисунок 2.4 – П-образный периодический потенциал. a, b – ширина ямы и барьера соответственно, a+b=T – трансляция одномерной решетки

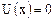Так как рассматривается одномерная модель, то . В области, где волновую функцию обозначим 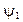, в области, где 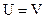– 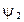. Объединенное уравнение Шредингера примет вид:

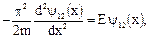(2.25)

или

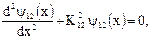(2.26)

где

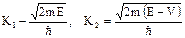. (2.27)

Рассмотрим случай нечетной функции:

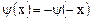. (2.28)

Следовательно, решение (2.25) для 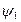имеет вид:

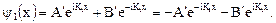(2.29)

Отсюда

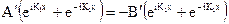, (2.30)

то есть

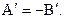(2.31)

Функция 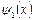(см.(2.29)) в этом случае примет вид:

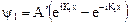. (2.32)

Рассмотрим функцию 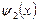для барьера при условии

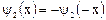, (2.33)

то есть (см. (2.26, 2.27))

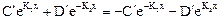. (2.34)

Отсюда

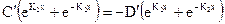, (2.35)

где (см. (2.24)) .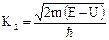

Следовательно 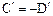и функция (см. (2.32)) примет вид:

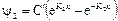. (2.36)

Из уравнений (2.31, 2.34) для случая нечетной волновой функции следует

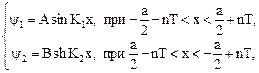(2.37)

где n – целое число.

Если волновая функция четная, что соответствует распространению бозонов, то есть

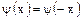. (2.38)

Решение волновых уравнений для ямы и барьера (2.24), (2.25) примет несколько другой вид. В этом случае:

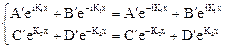, (2.39)

то есть

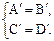(2.40)

Следовательно

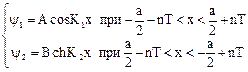. (2.41)

С учетом периодичности потенциалов из (2.39) и (2.40) следует, что решения уравнений Шредингера имеют вид:

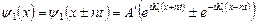, (2.42)

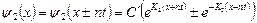, (2.43)

или

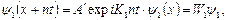(2.44)

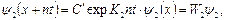(2.45)

что полностью соответствует теореме Блоха.

В уравнениях (2.44, 2.45) экспоненциальный множитель – это тоже волновая функция, так как 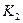<0 (см. (2.44)). Полученные уравнения для описания состояния электрона в поле периодического потенциала говорят о том, что волновая функция электрона в «яме» описывается такой же волновой функцией как и для свободного электрона, но вместо постоянной амплитуды 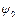появляется амплитудная волновая функция (см. (2.44)) 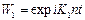. Следовательно, на состояние электрона влияют соседние ямы и в целом весь объем кристалла, так как n меняется от 1 до 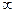, если кристалл бесконечный (в физическом смысле). То есть, строго говоря, состояние электрона в большом кристалле будет отличаться от состояния в более мелких частях, полученных при разрушении этого большого кристалла. Насколько велико влияние соседних ячеек периодического потенциала на состояние электрона? Этот вопрос требует дополнительного анализа.

Волновая (амплитудная) функция 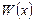(см. (2.44, 2.45)) перед волновой функцией электрона определяет влияние поля периодического потенциала на волновую функцию 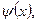то есть на поведение электрона. Функция 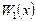периодическая с периодом от нуля до .

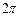Следовательно, максимальное значение показателя степени в этой амплитудной волновой функции в пределах ее одного периода равно

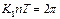. (2.46)

Отсюда (см. (2.27))

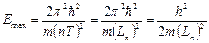. (2.47)

Здесь 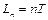определяет воздействие n ячеек в периодическом потенциале, влияющих на энергетическое состояние электрона в рассматриваемой ячейке. То есть из этой формулы следует, что при движении электрона в поле периодического потенциала основное влияние на него оказывают соседние «ямы и барьеры». Действительно

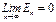. (2.48)

Кроме того, очевидно, что

.

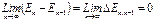Отсюда следует, что до некоторых значений 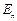, то есть в пределах n соседних периодов потенциала, электрон испытывает влияние соседних ячеек. Определив это «пороговое значение» 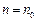можно говорить о том, что при 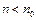весь «объем» одномерного кристалла влияет на движение электрона. Если 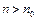, то, особенно при 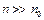, размерные эффекты при описании поведения электрона не играют роли. Следовательно, механизм протекания процессов в кристалле 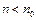при и при 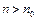различны.

В физике кристаллов рассматриваются процессы, на протекание которых влияние размеров не учитывается. В то же время хорошо известно, что такой двухмерный эффект, как поверхность кристалла, существенно влияет и на глубинные атомные слои. Причем это влияние может затрагивать от 5 до 15 внутренних атомных слоев [6].

В квантовой физике кристаллов используют различные методы описания состояний электронов, среди которых наиболее эффектные это метод сильной связи, метод ячеек, метод присоединенных плоских сил, метод Корринги – Кона – Ростокера МТ – потенциала (maffin-tin) и другие. Все они говорят о том, что в периодическом потенциале электрон испытывает влияние соседних ячеек.

В формуле (2.47) приведено 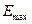для одномерного случая. Рассмотрев, для простоты, кубический кристалл, у которого три пространственных направления по координатам x,y,z, совпадающих с ребрами кубической ячейки, и повторив рассуждения для оси x,y получим, что для трехмерного случая можно записать значение объемной энергии 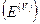в форме

. (2.49)

Как следует из вышесказанного, для каждого вещества имеется значение энергии 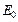разграничивающее механизмы протекания процессов. При 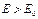размерные эффекты не играют роли и можно считать справедливым объемное приближение. При 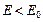необходимо учитывать размерные эффекты. Положив, что 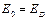, то есть равняется дебаевской энергии 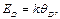тогда на основании формулы (2.49) получим предельный размер нанокристалла, рассчитываемый по формуле:

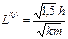. (2.50)

Легко убедиться, что полученная формула для расчета предельного размера нанокристалла абсолютно совпадает с выведенной ранее на основе иных, отличных от представлений о поле периодического потенциала, приближений.

Дата добавления: 2014-12-27