Для неравнобокого уголка 3 страница

6. Максимальное напряжение равно:

.

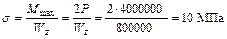Прочность балки обеспечена.

Задача 4.4

Для показанной на рисунке 4.11 а схемы определить допускаемую нагрузку 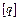. Построить эпюры и .

Дано: Балка изготовлена из стального профиля двутаврового сечения 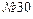(ГОСТ 8239-75); ;

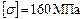Решение

1. Для заданной балки определяем реакции опор (рис. 4.11 б).

;

;

.

;

;

.

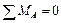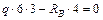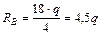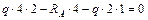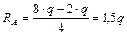Проверка

; ;

; .

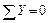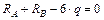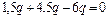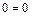2. Разбиваем заданную схему на участки. Составляем выражения для поперечных сил и изгибающих моментов в функции координаты .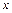

Участок I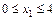

;

;

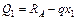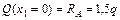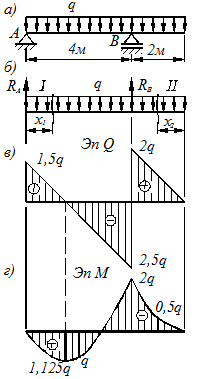
Рисунок 4.11

;

;

; ;

;

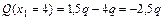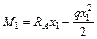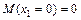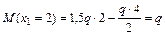Определим экстремальное значение изгибающего момента:

;

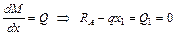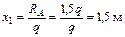
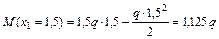
Участок II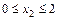

;

; ;

;

; ;

;

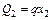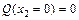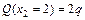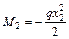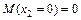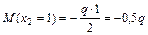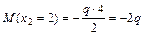3. По полученным данным строим эпюры и (рис. 4.11 в и г).

4. Определяем допускаемую нагрузку на балку, используя условие прочности при изгибе.

,

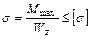где 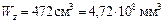– табличное значение для заданного профиля.

Тогда

;

;

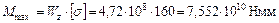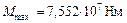Максимальная допускаемая распределенная нагрузка на балку:

;

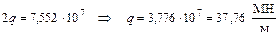Задача 4.5

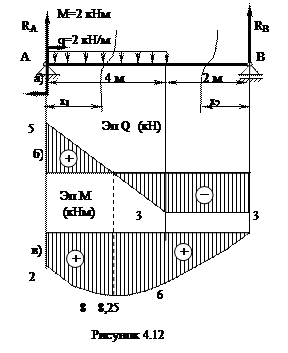
Для показанной на рисунке схемы построить эпюры поперечных сил Q и изгибающих моментов М, подобрать размеры поперечного сечения двутавровой балки, если [s] = 160 МПа

1. Определим значения реакции опор

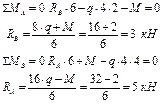
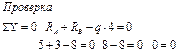
2. Разбиваем заданную схему на участки.

3. Определим значение поперечных сил Q и изгибающих моментов М на границах участков и в характерных точках.

Участок I	Участок II
0£ х1 £4	0£ х2 £2

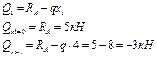
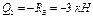
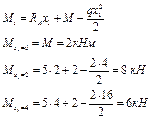
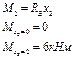
Определим экстремальное значение изгибающих моментов

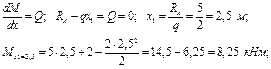
4. По полученным данным строим эпюры Q и М (рис. 4.12б, 4.12в)

Максимальный момент равен М_max = 8,25 кНм;

5. Определим размеры поперечного сечения двутавровой балки по сортаменту. Используем условие прочности при изгибе

.

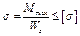Осевой момент сопротивления из условия прочности при изгибе равен

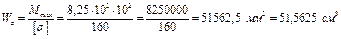
Из таблицы сортаментов определим размеры сечения двутавровой балки.

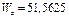см³ ÞΙ№ 12 с 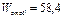см³

Определяем максимальное напряжение для выбранного двутавра

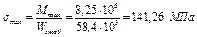
Недонапряжение составляет

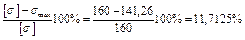
Прочность балки обеспечена

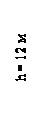
Эпюра нормальных напряжений показана на рис. 4.13

Рисунок 4.13

Задача 4.6

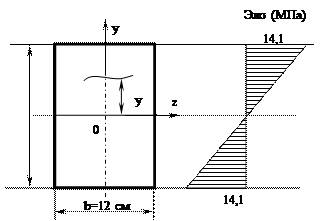
Для показанной на рисунке схемы построить эпюры поперечных сил Q и изгибающих моментов М (рис.4.13)

Сечение прямоугольное со сторонами b=12см; h=24 см.

Определить максимальное напряжение и построить эпюру s

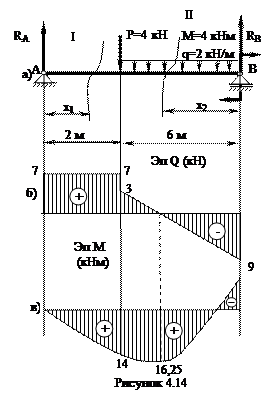
1. Определим значения реакции опор (рис.4.14 а)

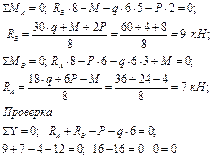
2. Разбиваем заданную схему на участки.

3. Для каждого участка схемы составляем выражения для поперечных сил Q и изгибающих моментов М в функции координаты «х». Определяем значения Q и М на границах участков.

Участок I	Участок II
0£ х1 £2	0£ х2 £6

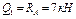
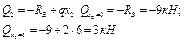
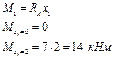
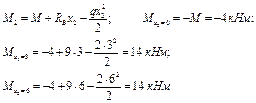
4. Определим экстремальное значение изгибающих моментов

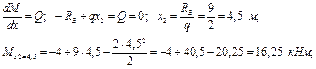
5. По полученным данным строим эпюры поперечных сил Q и изгибающих моментов М (рис. 4.14б, 4.14в)

6. Определим максимальное напряжение в прямоугольном поперечном сечении балки.

Используем условие прочности при изгибе

.

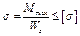Для прямоугольного сечения осевой момент сопротивления равен

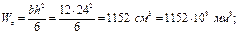
Максимальный изгибающий момент равен

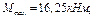
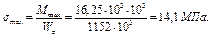
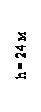
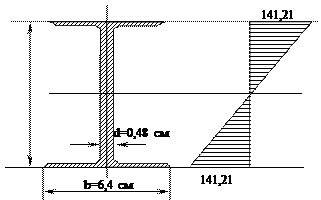
По полученным данным строим эпюру нормальных напряжений (рис. 4.15)

Рисунок 4.15

Задача 4.7

Для показанной на рисунке схемы построить эпюры поперечных сил Q и изгибающих моментов М.

Определить размеры поперечного сечения при соотношении диаметров d/D = 0,6, при[s] = 160 МПа (рис.4.16)

Построить эпюру нормальных напряжений s.

1. Разбиваем заданную схему на участки.

Для каждого участка схемы составляем выражения для поперечных силQ и изгибающих моментов М в функции координаты «х». Определяем значения Q и М на границах участков.

I

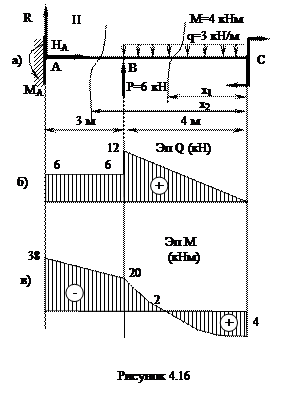
Участок I Участок II

0£ х₁ £4 4£ х₁ £7

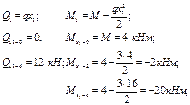
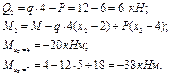
2. По полученным данным строим эпюры попеQ и М (рис. 4.16 б, 4.16 в)

3. Определим размеры поперечного сечения заданной балки. Используем условие прочности при изгибе.

.

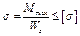Максимальный изгибающий момент равен.

4. Осевой момент сопротивления для кольцевого сечения определяется по формуле.

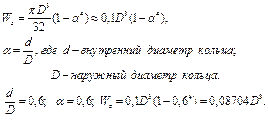
Осевой момент сопротивления из условия прочности равен.

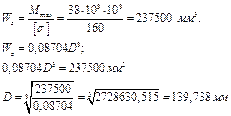
D=139,738 мм, округляя, принимаем D = 140 мм;

d = 0,6×140=84 мм.

Определим максимальное напряжение по принятым размерам поперечного сечения

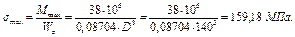
Недонапряжение составляет

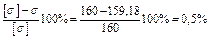
Прочность балки обеспечена.

По полученным данным строим эпюру нормальных напряжений (рис. 4.17)

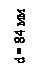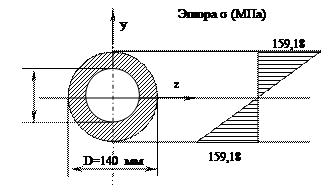Рисунок 4.17

4.6 Вопросы для самопроверки

1. Что называется прямым и косым изгибом?

2. Что называется чистым и поперечным изгибом?

3. Какие правила знаков приняты для каждого из внутренних усилий?

4. Какие внутренние усилия возникают при изгибе?

5. Как проверить правильность определения опорных реакций?

6. Что представляют собой эпюры поперечных сил и изгибающих моментов?

7. В каком порядке строится эпюра и ?

8. Какая дифференциальная зависимость существует между поперечной силой и интенсивностью распределенной нагрузки ?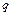

9. Как формулируется теорема Журавского?

10. Чему равна поперечная сила в сечениях бруса, в которых изгибающий момент достигает экстремальных значений?

11. Какой вид имеет эпюра изгибающих моментов на участке балки, во всех сечениях которого поперечная сила равна нулю?

12. Как связано изменение величины изгибающего момента с площадью эпюры ?

13. Как определяется экстремальное значение изгибающего момента?

14. Как формулируется гипотеза плоских сечений?

15. Что представляет собой нейтральный слой и нейтральная ось и как они расположены?

16. По какой формуле определяются нормальные напряжения в поперечном сечении балки при чистом изгибе и как они меняются по высоте балки?

17. Как записывается условие прочности при изгибе?

18. Какие типы задач решаются с помощью условия прочности при изгибе?

5 ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ЭНЕРГЕТИЧЕСКИМ МЕТОДОМ
(интеграл Мора и способ Верещагина)

При проработке этой темы нужно обратить особое внимание на определение перемещений при помощи способа Верещагина.

С целью обеспечения проработки этой темы ниже приводится подробное решение типовых задач на расчет балки и рамы; решения излагаются в той последовательности, которой необходимо придерживаться при выполнении контрольной работы.

Следует отметить, что в большинстве случаев при определении перемещений в балках, рамах и опорах по методу Мора, можно пренебречь влиянием продольных деформаций и сдвига, учитывая лишь перемещения, которые вызываются изгибом.

Поэтому формула Мора для плоской системы имеет вид

,

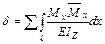где 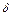– искомое обобщенное перемещение;

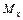– выражение изгибающего момента в функции координаты 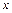только от заданной внешней нагрузки кНм;

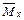– выражение изгибающего момента в функции координаты 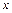от обобщенной единичной силы 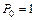или от 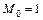, приложенной по направлению искомого перемещения;

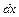– элемент длины бруса;

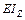– жесткость поперечного сечения рассматриваемого участка при изгибе.

Под обобщенной силой следует понимать любую нагрузку (сосредоточенные силы, сосредоточенные моменты, распределенные нагрузки), которая способна совершать работу на соответствующем обобщенном перемещении.

Если хотя бы одна из эпюр 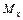, 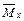имеет прямолинейный вид, то значение интеграла Мора для прямолинейного участка постоянной жесткости 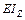можно вычислить по правилу Верещагина.

Правило Верещагина формулируется так, значение интеграла равно площади криволинейной эпюры изгибающего момента 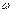, умноженной на ординату прямолинейной эпюры, взятую под центром тяжести криволинейной эпюры 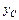или

;

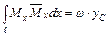Если одна из эпюр имеет вид ломанной, то интеграл Мора можно разбить на сумму 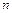интегралов, у которых одна из эпюр прямолинейна, тогда интеграл Мора может быть вычислен так:

,

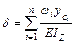где 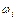– площадь нелинейной эпюры изгибающего момента от заданной внешней нагрузки, 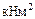на 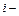том участке;

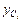– ордината прямолинейной эпюры изгибающих моментов под центром тяжести площади .

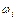Процедуру вычисления интеграла Мора по правилу Верещагина часто называют перемножением эпюр и символически изображают следующим образом.

,

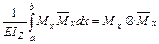здесь знак 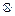означает вычисление интеграла Мора по способу Верещагина (перемножение эпюр).

При использовании способа Верещагина надо иметь в виду, что жесткость сечения бруса постоянна и если перемножаемые эпюры находятся по разные стороны от оси стержня ставится знак минус ("–").

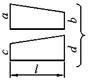
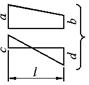
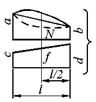
Способы сокращенного перемножения эпюр представлены на рис. 5.1.

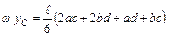
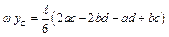
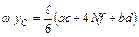
Рисунок 5.1

5.1 Статически определимые задачи

Задача 5.1

Для схемы (рис. 5.2) вычислить прогиб и угол поворота поперечного сечения на свободном конце консоли, используя интеграл Мора или способ Верещагина. Данные взять из таблицы 5.1

Порядок расчета

1. Для заданной нагрузки построить эпюру изгибающих моментов .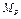

2. Приложить единичное усилие, соответствующее искомому прогибу и построить единичную эпюру изгибающих моментов.

3. Используя интеграл Мора или правило Верещагина, вычислить искомый прогиб.

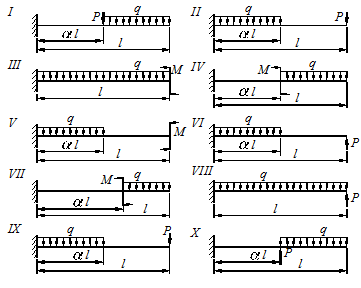
Рисунок 5.2

Таблица 5.1

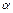
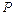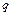№ строки	№ схемы	l, м		, кН	, кНм	, кН/м
	I		0,3
	II		0,4
	IV		0,2
	VI		0,4
	VII		0,2
	IX		0,4
	X		0,2
	III		0,3
	VIII		0,4
	V		0,3
	е	д	г	д	д	г

4. Приложить единичное усилие, соответствующее искомому углу поворота поперечного сечения и построить единичную эпюру изгибающих моментов.

5. Используя интеграл Мора или правило Верещагина, вычислить искомый угол поворота поперечного сечения.

Пример решения задачи 5.1.

Дано: ; ; .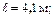

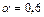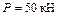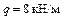Схема балки представлена на рисунке 5.3.

Определить прогиб 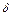и угол 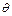поворота конца консоли, используя для вычисления интеграла Мора правило Верещагина.

1. Строим эпюры изгибающих моментов только от заданной внешней нагрузки (рисунок 5.3 а), определяя значения изгибающих моментов на границах участков и в характерных точках.

Участок I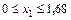

;

;

.

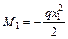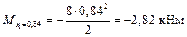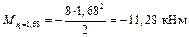Участок II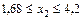

;

;

;

.

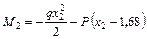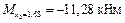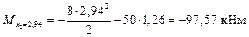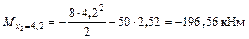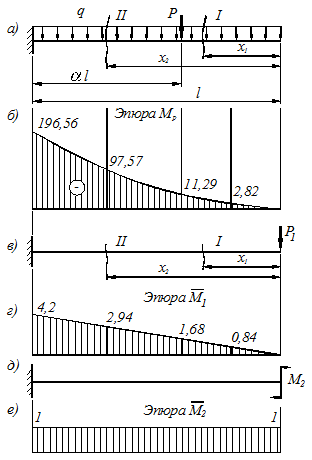
Рисунок 5.3

Эпюра изгибающих моментов 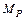приведена на рис. 5.3 б.

1. Для определения прогиба свободного конца балки в сечении 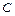прикладываем единичную силу 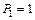(рис. 5.3 в).

Определяем значения изгибающих моментов на границах участков

Участок I	Участок II

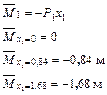
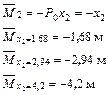
По полученным данным строим эпюру изгибающих моментов 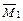от единичной силы 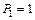(рис. 5.3 г).

Прогиб конца консоли, вычисляемый интегралом Мора, следует обозначить 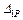, перемножаем эпюру 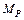с эпюрой 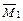по правилу Верещагина:

.

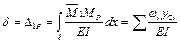Обе эпюры расположены с одной стороны, поэтому принимаем знак "+".

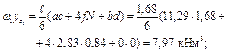
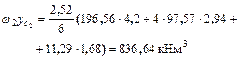
Прогиб конца консоли равен:

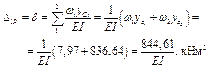
2. Для определения угла поворота свободного конца балки прикладываем единичный момент 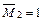рис. 5.3 д.

Строим эпюру 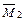на всей балке она постоянна и равна 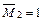. Эпюра приведена на рисунке 5.3 е.

Перемножаем грузовую эпюру 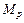(рис. 5.3 б) с эпюрой 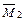(рис. 5.3 г)

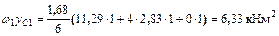
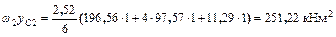
Искомый угол поворота сечения согласно обозначению эпюр есть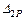

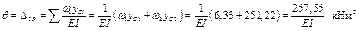
5.2 Статически неопределимые задачи

Расчет статически неопределимых балок и рам может выполняться методом сил, т.к. основными неизвестными являются силы. Пусть система 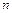– раз статически неопределима.

Заданная статически неопределимая система преобразуется в основную статически определимую систему, путем отбрасывания "лишних" с точки зрения статики связей и заменой их действия неизвестными силами 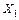, , 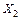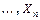. Эти силы называются основными неизвестными метода сил.

Условием эквивалентности основной системы и заданной является равенство нулю перемещений основной системы по направлению отброшенных связей.

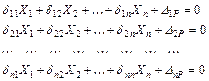
Здесь первая строка выражает требование равенства нулю перемещения по направлению силы 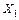, вторая – 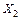и т.д., последняя по направлению 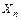. Коэффициенты 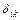это перемещения по направлению силы 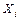, вызванные силой 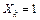. Они вычисляются интегралом Мора:

.

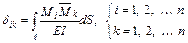Грузовые слагаемые 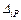являются перемещениями по направлению силы 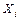, вызванные заданной внешней нагрузкой. Эти перемещения также вычисляются по формуле Мора:

.

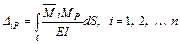Степень статической неопределимости может быть вычислена как разность:

,

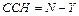где 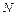– число неизвестных усилий;

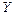– число возможных уравнений статики.

Дата добавления: 2014-12-27