Физический смысл второй производной

Если тело движется прямолинейно по закону, 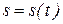, то вторая производная пути 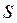по времени равна ускорению движения тела в данный момент времени : .

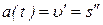Таким образом, первая производная характеризует скорость некоторого процесса, а вторая производная – ускорение того же процесса.

Пример 10. Точка движется по прямой по закону . Найти скорость и ускорение движения при .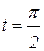

Решение. Скорость движения тела в данный момент времени равна производной пути 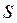по времени , а ускорение – второй производной пути 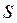по времени . Находим:

Пример 11. Скорость прямолинейного движения пропорциональна квадратному корню из пройденного пути (как, например, при свободном падении). Доказать, что это движение происходит под действием постоянной силы.

Решение. По закону Ньютона, сила 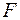, вызывающая движение, пропорциональна ускорению, т.е.

.

Согласно условию, 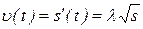. Дифференцируя это равенство, найдем .

Следовательно, действующая сила .

Приложение производной к исследованию функций

Условия постоянства функции. Дифференцируемая функция

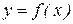постоянна на промежутке X тогда и только тогда, когда внутри X.

Условие возрастания функции. Дифференцируемая функция 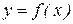монотонно возрастает на промежутке Х тогда и только тогда, когда её производная не отрицательна внутри этого промежутка: 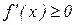причём производная обращается в нуль в конечном числе точек, лежащих внутри Х.

Это условие геометрически означает, что касательная к графику монотонно возрастающей функции образует с положительным направлением оси Ох острый угол или параллельна ей (рисунок 5).

Условие убывания функции. Дифференцируемая функция 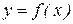монотонно убывает на промежутке Х тогда и только тогда, когда ее производная не положительна внутри этого промежутка: 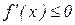, причем производная обращается в нуль в конечном числе точек, лежащих внутри Х.

Это условие геометрически означает, что касательная к графику монотонно убывающей функции образует с положительным направлением оси Ох угол или параллельна ей (рисунок 6).

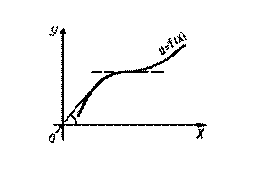
Рисунок 5 Рисунок 6

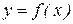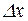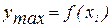Экстремумы функции. Говорят, что функция имеет максимум в точке х ₁,если значение функции в этой точке больше, чем ее значения во всех точках, достаточно близких к х ₁, т.е. если для любых , как положительных, так и отрицательных, но достаточно малых по модулю. Таким образом, – точка максимума, а – максимум функции.

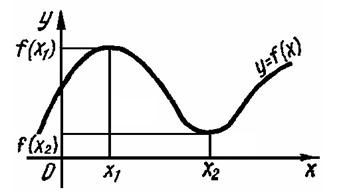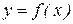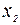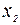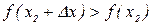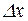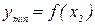Говорят, что функция имеет минимум в точке , если значение функции в этой точке меньше, чем ее значения во всех точках, достаточно близких к , т.е. если для любых , как положительных, так и отрицательных, но достаточно малых по модулю. Таким образом, – точка минимума, а – минимум функции (рисунок 7).

Если в некоторой точке функция имеет максимум или минимум, то говорят, что в этой точке имеет место экстремум.

Рисунок 7

Значение функции в этой точке называется экстремальным.

Замечание. Следует помнить: 1 что максимум (минимум) не является обязательно наибольшим (наименьшим) значением, принимаемым функцией;

2 функции может иметь несколько максимумов или минимумов;

3 функция, определенная на отрезке, может достигать экстремума только во внутренних точках этого отрезка.

Необходимое условие экстремума. Если функция 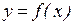имеет

экстремум при 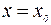, то ее производная в этой точке равна нулю или

бесконечности, либо вовсе не существует, при этом сама функция в точке определена.

Из этого следует, что точки экстремума функции следует разыскивать только среди тех, в которых ее первая производная равна нулю, или бесконечности, или не существует. Эти точки называются критическими точками I рода.

Этот признак экстремума является только необходимым. Поэтому, определив критические точки I рода, каждую из них в отдельности исследовать на

основании достаточных условий экстремума.

Первое достаточное условие существования экстремума функции. Пусть точка является критической точкой I рода функции 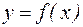, а сама функция дифференцируема во всех точках некоторого промежутка, содержащего эту точку (за исключением, возможно, самой этой точки). Тогда:

1 если при переходе слева направо через критическую точку I рода первая производная меняет знак с плюса на минус, то в этой точке функция достигает максимума, т. е. – точка максимума,

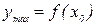
2 если при переходе слева направо через критическую точку I рода 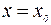первая производная меняет знак с минуса на плюс, то в этой точке функция достигает минимума, т. е. – точка минимума, .

3 если при переходе через критическую точку 1 рода первая производная не меняет знака, то в этой точке экстремума нет.

Для исследования функции на экстремум по первой производной следует:

1 найти область определения функции;

2 найти первую производную функции и критические точки I рода;

3 отметить границы области определения и критические точки I рода на числовой прямой;

4 исследовать знак производной в каждом из полученных интервалов;

5 выписать точки экстремумов и вычислить экстремумы функции.

Пример 12. Найти экстремумы функции .

Решение. 1 Областью определения функции служит множество всех действительных чисел, т. е. .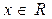

2 Функция имеет производную всюду, поэтому определяем критические точки из условия . Находим производную:

3 Отмечаем эти критические точки на числовой прямой (рисунок 8).

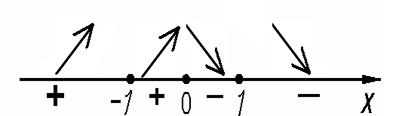
Рисунок 8

4 Исследуем знак производной 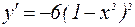в каждом из полученных интервалов:

5 Точка х = 0 – точка максимума, так как при переходе через нее слева направо производная меняет знак плюса на минус: 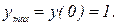Точки х = −1 и х = 1 не являются точками экстремума.

Второе достаточное условие существования экстремума функции. Если в точке х=х₀ первая производная функции равна нулю (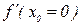), а вторая производная отлична от нуля, то х=х₀ ‌– точка экстремума.

При этом, если вторая производная в этой точке положительна (), то х=х₀ – точка минимума; если вторая производная в этой точке отрицательна (), то х=х₀ – точка максимума.

Для исследования функции на экстремум по первой и второй производной следует:

1 найти область определения функции;

2 найти первую производную функции и стационарные точки, т. е. точки, в которых она обращается в нуль;

3 найти вторую производную функции и исследовать ее знак в каждой стационарной точке;

4 выписать точки экстремума и вычислить (если нужно) экстремумы функции.

Пример 13. Найти экстремумы функции .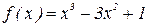

Решение. 1 Областью определения функции служит множество всех действительных чисел, т.е. .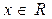

2 Функция имеет производную всюду, поэтому критические точки определяем из условия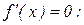

4 Находим вторую производную функции 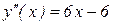. Исследуем знак второй производной в каждой критической точке 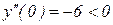; значит, х = 0 – точка максимума,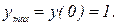 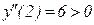; значит, х = 2 – точка минимума,

Наибольшее и наименьшее значения функции. Наибольшим значением функции называется самое большое, а наименьшим значением – самое меньшее из всех ее значений.

Функция может иметь только одно наибольшее значение и только одно наименьшее значение или может не иметь их совсем.

Нахождение наибольшего и наименьшего значений непрерывных функций основывается на следующих свойствах этих функций:

1 если в некотором открытом промежутке 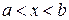(конечном или беско-

нечном) функция непрерывна и имеет только один экстремум и если

это максимум, то он является наибольшим значением функции, а если минимум - наименьшим значением функции в этом промежутке;

2 если функция 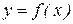непрерывна на отрезке , то она обязательно имеет на этом отрезке наибольшее и наименьшее значения. Эти значения достигаются ею или в точках экстремума, лежащих внутри отрезка, или на концах этого отрезка.

Поэтому, чтобы найти наибольшее и наименьшее значения , где она непрерывна, следует:

1 найти экстремумы функции на данном отрезке;

2 найти значения функции на концах отрезка: ;

3 из всех найденных значений выбрать наибольшее и наименьшее.

Пример 14. Найти наибольшее и наименьшее значение функции на отрезке .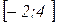

Решение. 1 Найдем экстремумы функции, для чего найдем производную функции и критические точки I рода из условия :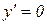

,

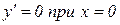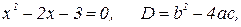
Отметим критические точки I рода х = -1, х = 0, х = 3 на числовой прямой (рисунок 9).

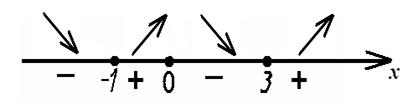
Рисунок 9

Исследуем знак производной в каждом из полученных интервалов: .

Таким образом,

2 Найдем значения функции на концах отрезка:

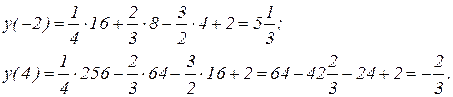
3 Итак, наибольшее значение функции , а наименьшее значение функции .

Пример 15. Число 10 разбить на два положительных слагаемых так, чтобы сумма их кубов была наименьшей.

Решение. Пусть одно из слагаемых равно х, тогда другое слагаемое есть 10 − х. Сумма кубов этих слагаемых равна:

Наименьшее значение этой функции и надо определить.

1 Областью определения функции S являются положительные значения х, т.е. х >0.

2 Находим производную:

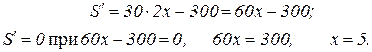
З Находим вторую производную: при х = 5 функция S имеет минимум, который и является наименьшим значением функции.

Итак, число 10 надо разложить на два равных слагаемых: 5 и 5.

Пример 16. Закон прямолинейного движения тела задан уравнением 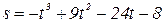( 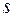– в метрах, 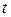– в секундах). Найти максимальную скорость движения тела.

Решение. Скорость движения тела в данный момент времени равна производной пути по времени :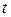

.

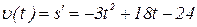Исследуем эту функцию на экстремум с помощью второй производной: . Вторая производная отрицательна; следовательно, скорость является наибольшей при 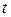=3.

Максимальная скорость движения составляет

м/с.

Направление вогнутости и точки перегиба кривой. Говорят, что на промежутке 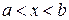кривая обращена выпуклостью вверх или выпукла (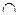) если она лежит, ниже касательной, проведенной в любой ее точке (рисунок 10).

Говорят, что на промежутке 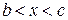кривая обращена выпуклостью вниз или вогнута (), если она лежит выше касательной, проведенной в любой ее

точке (рисунок 10).

Точкой перегиба непрерывной кривой называется точка А (рисунок 10), при переходе через которую кривая меняет свою вогнутость на выпуклость или наоборот.

Достаточное условие выпуклости (вогнутости) кривой.

Рисунок 10

График дифференцируемой функции является выпуклым на промежутке 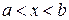, если вторая производная функция отрицательна в каждой точке этого промежутка: 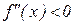при .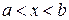

График дифференцируемой 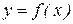функции является вогнутым на промежутке 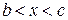,если вторая производная функции положительна в каждой точке этого промежутка: 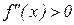при .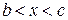

Точки, в которых вторая производная функции равна нулю, или бесконечности, или не существует, называются критическими точками II рода.

Если при переходе через критическую точку II рода х = х₀ вторая производная функции меняет знак, то х = х ₀ – абсцисса точки перегиба. Ордината точки перегиба равна значению функции в точке х₀. Точка (х ₀, ) – точка перегиба графика функции .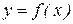

Чтобы найти направление вогнутости и точки перегиба кривой, следует:

1 найти область определения функции;

2 найти вторую производную функции и критические точки II рода;

3 отметить границы области определения и критические точки II рода на числовой прямой;

4 исследовать знак второй производной в каждом из полученных интервалов;

5 записать промежутки выпуклости и вогнутости, абсциссу точки перегиба и вычислить ее ординату.

Пример 17. Определить направление вогнутости и точки перегиба кривой .

Решение. 1 Областью определения функции служит множество всех действительных чисел, т.е. .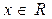

2 Найдем вторую производную функции и критические точки II рода из условия :

3 Отметим критические точки 11 рода х = −2 и х = 1 на числовой прямой (рисунок 11).

	Рисунок 11		Рисунок 12

4 Исследуем знак второй производной в каждом из полученных интервалов: .

5 Кривая вогнута при кривая выпукла при 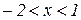. Точки перегиба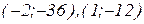

Общая схема исследования функций и построения их графиков

1 Найти область определения функции.

2 Выяснить вопрос о четности, нечетности и периодичности функции.

3 Найти точки пересечения графика функции с осями координат.

4 Найти промежутки монотонности и эксремумы функции.

5 Найти направление вогнутости и точки перегиба.

6 Построить график функции.

Дата добавления: 2014-12-27