
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Аффинные преобразования
|
|
|
|
2.2.1 Общие аффинные соответствия
Рассмотрим цепь последовательных параллельных проецирований:  (рисунок 2.5).
(рисунок 2.5).

Рисунок 2.5 – Цепь последовательных параллельных проецирований
Таким образом, представлен ряд перспективно-аффинных преобразований:  ,
, 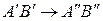 ,
,  Результатом можно записать:
Результатом можно записать: 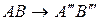 . Полученное результирующее соответствие плоскостей
. Полученное результирующее соответствие плоскостей 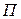 и
и 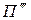 называется аффинным. Здесь также сохраняются коллинеарность и простое отношение трех точек.
называется аффинным. Здесь также сохраняются коллинеарность и простое отношение трех точек.
Тогда аффинное преобразование  можно записать как произведение родственных преобразований
можно записать как произведение родственных преобразований  :
:  .
.
Резюме: аффинные преобразования – коллинеарные, в качестве основных инвариантов рассматривает два равносильных свойства: простое отношение трех точек 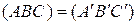 и параллельность прямых
и параллельность прямых 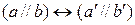 .
.
2.2.2 Частные случаи аффинного преобразования плоскости
Рассмотрим два родственных треугольника (соответственные треугольники перспективно-аффинного преобразования) 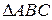 и
и 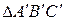 (рисунок 2.6).
(рисунок 2.6).

Рисунок 2.6 – Соответственные треугольники перспективно-аффинного
преобразования
На этом рисунке отрезки  ,
, 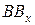 ,
,  считаются положительно направленными, так как положительное направление задает
считаются положительно направленными, так как положительное направление задает  . Тогда отрезки
. Тогда отрезки 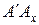 ,
,  ,
,  имеют противоположное, т.е. отрицательное направление.
имеют противоположное, т.е. отрицательное направление.
При этом, вводится коэффициент преобразования  , который определяется (или задается) как отношение:
, который определяется (или задается) как отношение:
 . (2.1)
. (2.1)
Для перспективно-аффинного преобразования  .
.
Ниже приведены другие частные случаи аффинного преобразования.
2.2.2.1 Косая симметрия
Для этого преобразования  ,
,  ,
,  (рисунок 2.7), поэтому в соответствии с выражением (2.1)
(рисунок 2.7), поэтому в соответствии с выражением (2.1) 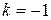 .
.

Рисунок 2.7 – Косая симметрия
Если, направление  оказалось бы перпендикулярным прямой
оказалось бы перпендикулярным прямой 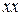 , то имело бы место осевая симметрия (отражение относительно этой прямой), которое является ортогональным преобразованием, или движением. Нетрудно видеть, что ортогональная и косая симметрия являются инволюционным преобразованием, так как при таком преобразовании безразлично к какой плоскости отнесены прообраз и образ (см. рисунок 2.8, точки
, то имело бы место осевая симметрия (отражение относительно этой прямой), которое является ортогональным преобразованием, или движением. Нетрудно видеть, что ортогональная и косая симметрия являются инволюционным преобразованием, так как при таком преобразовании безразлично к какой плоскости отнесены прообраз и образ (см. рисунок 2.8, точки  и
и  ).
).
|
|
|
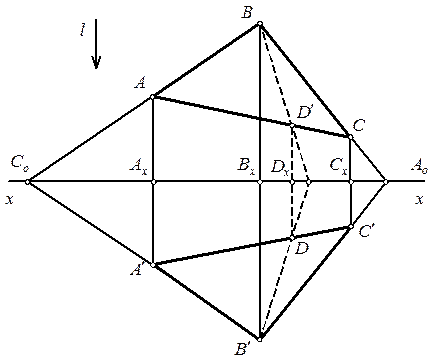
Рисунок 2.8 – Ортогональная симметрия
2.2.2.2 Косое сжатие и растяжение
Для косого сжатия коэффициент преобразования принимает следующие значения:  . Пример построения сжатия
. Пример построения сжатия 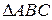 к прямой
к прямой 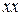 показан на рисунке 2.9.
показан на рисунке 2.9.

Рисунок 2.9 – Косое сжатие
Если коэффициент  , то имеет место растяжения от прямой
, то имеет место растяжения от прямой  (рисунок 2.10).
(рисунок 2.10).

Рисунок 2.10 – Косое растяжение
Для значения  все точки плоскости остаются на месте, такое преобразование называется тождественным. (
все точки плоскости остаются на месте, такое преобразование называется тождественным. ( ,
,  ,
,  ).
).
Аналогично можно рассматривать ортогональное сжатие и растяжение по отношению к прямой  , к которой направление
, к которой направление  перпендикулярно.
перпендикулярно.
2.2.2.3 Гомотетия
Рассмотрим другой частный случай аффинного преобразования, который называется гомотетией. Гомотетию можно рассматривать как равномерное растяжение и как равномерное сжатие к точке (прямая гомотетия). Для равномерного сжатия коэффициент преобразования (коэффициент гомотетии)  , для равномерного растяжения
, для равномерного растяжения  . При значении
. При значении  , имеет место тождественное преобразование (все точки плоскости остаются на месте). Кроме того, различают еще и обратную гомотетию, для которой
, имеет место тождественное преобразование (все точки плоскости остаются на месте). Кроме того, различают еще и обратную гомотетию, для которой  , однако, при значении
, однако, при значении  , получаем более частный случай – центральную симметрию. Рассмотрим перечисленные преобразования плоскости более подробно.
, получаем более частный случай – центральную симметрию. Рассмотрим перечисленные преобразования плоскости более подробно.
Пример прямой гомотетии представлен рисунком 2.11.
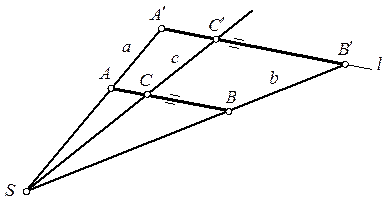
Рисунок 2.11 – Построение точки 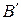 в прямой гомотетии
в прямой гомотетии
Любой вид гомотетии задается центром гомотетии (точка  ) и парой соответственных точек (даны точки
) и парой соответственных точек (даны точки 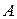 и
и 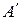 , расположенные на слабоинвариантной прямой
, расположенные на слабоинвариантной прямой 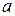 , проходящей центр гомотетии
, проходящей центр гомотетии  )[1]. При задании еще одной точки, например
)[1]. При задании еще одной точки, например 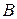 , можно построить ее образ
, можно построить ее образ 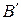 . Для этого необходимо через центр гомотетии
. Для этого необходимо через центр гомотетии  и точку
и точку 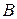 провести слабоинвариантную прямую
провести слабоинвариантную прямую 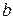 , а из точки
, а из точки 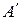 провести прямую
провести прямую  . Тогда, точка
. Тогда, точка 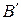 определится, как результат пересечения прямой
определится, как результат пересечения прямой 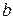 и
и  :
:  .
.
|
|
|
Отсюда заключаем, каждая прямая 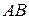 преобразуется в прямую
преобразуется в прямую  . Кроме того, прямая
. Кроме того, прямая 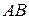 , не проходящая через центр гомотетии
, не проходящая через центр гомотетии  , переходит в параллельную ей прямую
, переходит в параллельную ей прямую  .
.
В гомотетии сохраняется простое отношение трех точек 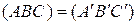 , что можно проследить по рисунку 2.11:
, что можно проследить по рисунку 2.11:
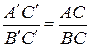 .
.
Коэффициент гомотетии будет определяться отношением
 .
.
На рисунке 2.12 показаны два соответственных треугольника 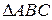 и
и 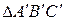 в прямой гомотетии (гомотетичные треугольники).
в прямой гомотетии (гомотетичные треугольники).

Рисунок 2.12 – Соответственные треугольники в прямой гомотетии
Здесь следует отметить, что прямая гомотетия преобразует каждую фигуру (например, 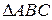 ) в подобную и подобно расположенную фигуру (
) в подобную и подобно расположенную фигуру (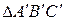 ). Величины углов не изменяется в гомотетии, так как каждый угол переходит в угол с соответственно параллельными сторонами.
). Величины углов не изменяется в гомотетии, так как каждый угол переходит в угол с соответственно параллельными сторонами.
В обратной гомотетии заданные соответственные точки, расположенные на слабоинвариантной прямой, всегда находятся по разные стороны от центра гомотетии  .
.
Однако гомотетия не является еще преобразованием подобия. Для преобразования подобия необходимо последовательно выполнить гомотетию и как минимум одно преобразование движения (трансляцию, поворот, осевую или центральную симметрию). Композицию этих преобразований можно выполнить и в обратном порядке.
На рисунке 2.13 представлено построение треугольника 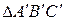 соответственного треугольнику
соответственного треугольнику 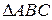 в обратной гомотетии. Эту гомотетию можно рассматривать и как композицию двух преобразований: сначала выполнить прямую гомотетию, а затем – центральную симметрию относительно центра гомотетии (можно выполнить эти преобразования и в обратной последовательности).
в обратной гомотетии. Эту гомотетию можно рассматривать и как композицию двух преобразований: сначала выполнить прямую гомотетию, а затем – центральную симметрию относительно центра гомотетии (можно выполнить эти преобразования и в обратной последовательности).
 |
Рисунок 2.13 – Соответственные треугольники в обратной гомотетии
На рисунке 2.14 выполнена сначала центральная симметрия, а затем прямая гомотетия:  .
.

Рисунок 2.14 – Обратная гомотетия, как композиция преобразований
2.2.2.4 Центральная симметрия
|
|
|
Центральная симметрия является частным случаем обратной гомотетии. Это преобразование является преобразованием второго рода, так как меняется ориентация фигуры на противоположную: если при обходе 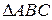 мы движемся против хода часовой стрелки (рисунок 2.14), то при обходе
мы движемся против хода часовой стрелки (рисунок 2.14), то при обходе 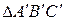 – по часовой, т.е. в обратном направлении.
– по часовой, т.е. в обратном направлении.
Свойства этого преобразования знакомы из средней школы.
2.2.2.5 Сдвиг
Рассмотрим сдвиг, т.е. еще одно аффинное преобразование, для которого слабо инвариантные прямые линии параллельны двойной (неподвижной, инвариантной) прямой, которая называется осью сдвига (рисунок 2.15).

Рисунок 2.15 – Преобразование сдвига
В этом случае коэффициентом сдвига называется отношение

Вместо коэффициента сдвига  часто задают угол сдвига
часто задают угол сдвига
 ,
,
где 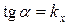 .
.
Угол  считается направленным:
считается направленным:
– положительно направленный сдвиг – это сдвиг вправо, т.е. присваивается знак «+», например от  к
к  ;
;
– отрицательно направленный сдвиг – это сдвиг влево, т.е. угол  и величина
и величина  имеют знак «–».
имеют знак «–».
При  (и
(и  ) имеем тождественное преобразование.
) имеем тождественное преобразование.
2.2.3 Аффинное преобразование как произведение преобразований
Пусть имеется аффинное соответствие двух плоских полей: 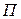 и
и 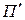 установленное парой соответственных треугольников
установленное парой соответственных треугольников 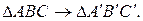 Покажем, что данное аффинное преобразование можно выразить как произведение (умножение, композицию) преобразований:
Покажем, что данное аффинное преобразование можно выразить как произведение (умножение, композицию) преобразований:  , где
, где 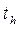 – гомотетия,
– гомотетия,  – движение,
– движение,  – перспективно-аффинное преобразование (рисунок 2.16).
– перспективно-аффинное преобразование (рисунок 2.16).

Рисунок 2.16 – Аффинное преобразование 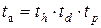
В соответствии с этим рисунком выполним следующие действия:
– устанавливаем перспективно- аффинное соответствие 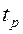 с осью родства
с осью родства 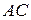 и парой соответственных точек:
и парой соответственных точек: 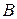 и
и  , следовательно,
, следовательно,  , где
, где  , а
, а  подобен
подобен 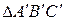 ;
;
– выполняя 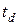 , переместим плоскость
, переместим плоскость 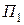 в новое положение так, чтобы вершина
в новое положение так, чтобы вершина 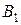 совпала с
совпала с 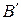 , а угол
, а угол  совместился бы с углом
совместился бы с углом  ;
;
– произведем преобразование гомотетии 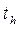 с центром
с центром 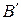 , и коэффициентом
, и коэффициентом
 .
.
В результате получим 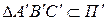 .
.
Таким образом, из двух произвольных заданных треугольников 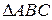 и
и 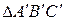 каждый можно считать аффинно-соответственным другому.
каждый можно считать аффинно-соответственным другому.
|
|
|
Другим примером этого положения может служить преобразование  (рисунок 2.17).
(рисунок 2.17).

Рисунок 2.17 – Аффинное преобразование 
Выполнение этой композиции преобразований понятно из данного рисунка:
– осуществляется первое перспективно-аффинное преобразование  (родство), для которого ось родства проходит через прямую
(родство), для которого ось родства проходит через прямую 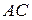 , отрезок
, отрезок  в произвольном направлении, тогда
в произвольном направлении, тогда  ;
;
– выполняется второе перспективно-аффинное преобразование  , здесь ось родства
, здесь ось родства  , точка
, точка  является геометрическим местом пересечения дуг окружностей соответственно радиуса
является геометрическим местом пересечения дуг окружностей соответственно радиуса  и
и  , тким образом получается
, тким образом получается 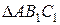 ;
;
– производится преобразование движения 
 .
.
Рассмотрим теорему.
Теорема. Существует лишь одно аффинное преобразование 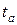 , которое переводит треугольник
, которое переводит треугольник 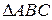 одной плоскости
одной плоскости 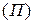 в
в 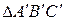 второй плоскости
второй плоскости 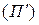 .
.
 Доказательство.
Доказательство.
Пусть точка 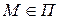 и
и  (рисунок 2.18), тогда имеется равенство простого отношения трех точек
(рисунок 2.18), тогда имеется равенство простого отношения трех точек 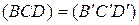 . Следовательно, точка
. Следовательно, точка  , соответственная точке D, однозначно определяется на прямой линии
, соответственная точке D, однозначно определяется на прямой линии  .
.
Кроме того, наблюдается равенство простого отношения трех точек  , тогда и точка
, тогда и точка 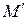 однозначно определяется на прямой линии
однозначно определяется на прямой линии 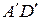 , которая соответствует прямой
, которая соответствует прямой  . Таким образом, в аффинном преобразовании одной плоскости в другую переводящим
. Таким образом, в аффинном преобразовании одной плоскости в другую переводящим 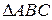 в
в 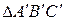 , соответствие точек определяется единственным образом.
, соответствие точек определяется единственным образом.

Рисунок 2.18 – Аффинное преобразование 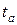 :
: 
Следовательно, не может быть двух аффинных преобразований, переводящих 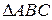 в
в 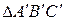 , которые не были бы тождественными.
, которые не были бы тождественными.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 5286; Нарушение авторских прав?; Мы поможем в написании вашей работы!