
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЗАНЯТИЕ 16. Контрольная работа №2. Прием части-2 БДЗ
|
|
|
|
ЗАНЯТИЕ 15. Однородные системы уравнений. Общее решение системы уравнений, Фундаментальная система решений. Связь решения неоднородной системы уравнений и соответствующей ей однородной системы.
☺ ☻ ☺
Как и в общем случае исследования системы неоднородных линейных уравнений, использование теоремы Кронекера–Капелли в частном случае исследования системы линейных однородных уравнений также плодотворно. Общая схема решения:
A 1 *: Вычисляем ранг: 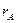 матрицы системы.Так как для однородной системы уравнений
матрицы системы.Так как для однородной системы уравнений 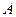 =
= 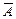 , то всегда выполняется
, то всегда выполняется 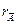
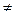
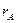 . Однородная система уравнений всегда совместна. Пусть
. Однородная система уравнений всегда совместна. Пусть 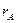 =
= 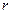 . Это значит, что определён базовый минор M
. Это значит, что определён базовый минор M 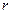 матрицы системы.
матрицы системы.
A 2 *: В системе уравнений оставляем только те 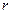 уравнения-строки, которые попали в базовый минор: остальные являются следствием выделенных.
уравнения-строки, которые попали в базовый минор: остальные являются следствием выделенных.
A 3 *: В левой части каждого из оставшихся для дальнейшего решения уравнений оставляем те 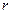 столбцов с неизвестными, которые попали в базовый минор: остальные неизвестные объявляем свободными и соответствующие столбцы с ними переносим в правую часть.
столбцов с неизвестными, которые попали в базовый минор: остальные неизвестные объявляем свободными и соответствующие столбцы с ними переносим в правую часть.
A 4 *: Находим решения преобразованной системы уравнений, применяя формулы Крамера: определитель преобразованной системы не равен нулю!
A 5 *: Полученное решение системы называют общим: вычисленные по формулам Крамера неизвестные выражаются через свободные неизвестные. Присваивая свободным неизвестным произвольные значения, получаем частные решения.
Замечание: отметим, что свободных неизвестных 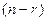 : их можно воспринимать как число степеней свободы процесса; вычисляемых неизвестных –
: их можно воспринимать как число степеней свободы процесса; вычисляемых неизвестных – 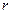 .
.
••• ≡ •••
Пример 15 – 1: Исследовать систему уравнений: 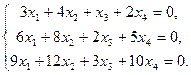 Найти общее решение и одно частное.
Найти общее решение и одно частное.
|
|
|
Решение:
1). Составим матрицу: 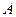 =
= 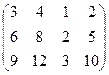 и найдём её ранг. Выделим для окаймления минор (не равен нулю), расположенный в правом верхнем углу матрицы:
и найдём её ранг. Выделим для окаймления минор (не равен нулю), расположенный в правом верхнем углу матрицы:
3). Окаймляющие миноры будем обозначать: 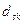 , где
, где 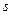 – указывает номер отмеченной для окаймления строки,
– указывает номер отмеченной для окаймления строки, 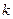 – указывает номер отмеченного для окаймления столбца. Тогда можем записать:
– указывает номер отмеченного для окаймления столбца. Тогда можем записать:
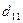 =
= 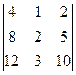 =4·
=4· 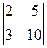 –8·
–8· 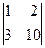 +12·
+12· 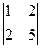 = m 1· (5) – h 1· (4) + g 1· (1) =
= m 1· (5) – h 1· (4) + g 1· (1) =
=4·(5)–8·(4)+12·(1) =0;
Замечание: параметры: m 1, h 1, g 1 изменяются при переходе к минорам 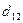 ,
, 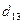 , числа: (5), (4), (1) не изменяются. Это позволяет применить единый шаблон вычислений!
, числа: (5), (4), (1) не изменяются. Это позволяет применить единый шаблон вычислений!
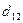 =
= 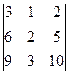 = m 2· (5) – h 2· (4) + g 2· (1) = 3·(5)–6·(4)+9·(1) =0;
= m 2· (5) – h 2· (4) + g 2· (1) = 3·(5)–6·(4)+9·(1) =0;
4). Так как все миноры 3-го порядка оказались равными нулю, то 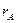 =2.
=2.
5). Учитывая расположение не равного нулю минора, 3-е уравнение отбрасываем и свободными неизвестными объявляем 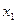 и
и 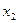 :
:
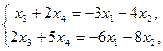
далее применяем правило Крамера:
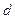 =1;
=1; 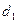 =
= 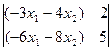 =
= 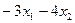 ;
; 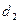 =
= 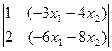 =0.
=0.
6). Общее решение системы: 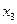 =
= 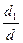 =
= 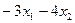 ;
;  =
= 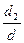 =0; частное решение получим при значениях:
=0; частное решение получим при значениях: 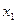 =1,
=1, 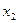 =–1, →
=–1, → 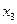 =1,
=1,  =0.
=0.
Ответ: общее решение: 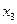 =
= 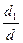 =
= 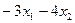 ;
;  =
= 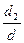 =0; частное решение: (1,–1,1,0).
=0; частное решение: (1,–1,1,0).
Пример 15 – 2: Исследовать систему уравнений: 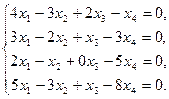 Найти общее и частное решение.
Найти общее и частное решение.
Решение:
1). Применим пошаговый процесс метода Гаусса:
| -3 | -1 | -1 | -1 | |||||||
| -2 | -3 | -1 | ||||||||
| -1 | -5 | =(1)→ | -1 | =(2)→ | ||||||
| -3 | -8 | -1 | -7 |
| -1 | -1 | -7 | ||||||||
| -2 | ||||||||||
| -2 | =(3)→ | =(4)→ | ||||||||
| -9 | -9 |
Выполнены операции: (1): [R4]–[R1]; [R1]–[R2]; [R2]–[R3]; [R3]–[R4]. (2): [R2]–[R1]; [R3]–[R1]; [R4]–[R1]. (3): [R3]–[R1]; [R2] делим на (–2); [R1]–[R2]; [R1]–[R4]. (4): раскрываем полученный результат.
2). Видим: 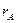 =3. Свободной неизвестной объявляем
=3. Свободной неизвестной объявляем  =
= 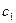 .
.
3). Из уравнения-строки [R4] запишем: 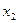 =9
=9 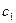 ; из строки [R2]:
; из строки [R2]: 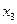 =0; [R4] запишем:
=0; [R4] запишем: 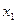 =7
=7 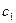 . Произвольная величина
. Произвольная величина 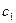 определяет бесчисленное множество решений заданного уравнения.
определяет бесчисленное множество решений заданного уравнения.
|
|
|
Ответ: общее решение: (7 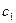 ;9
;9 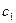 ;0;
;0; 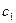 )=
)= 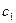 (7,9, 0;1).
(7,9, 0;1).
Пример 15 – 3: Найти общее решение системы уравнений: 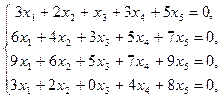 и фундаментальную систему решений.
и фундаментальную систему решений.
Решение:
1). Применим пошаговый процесс метода Гаусса:
| -1 | -3 | |||||||||||
| =(1)→ | -2 | -6 | =(2)→ | |||||||||
| -1 |
| -1 | -3 | -1 | -3 | |||||||||
| =(3)→ | =(4)→ | |||||||||||
Выполнены операции: (1): [R4]–[R1]; [R2]–[R1]·2; [R3]–[R1]·3. (2): [R3]–[R2]·2; [R4]–[R2]. (3): [R1]–[R2]. (4): раскрываем полученный результат.
2). Видим: 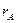 =2. Пусть
=2. Пусть 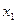 ,
, 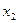 ,
,  свободные неизвестные. Раскрываем таблицу:
свободные неизвестные. Раскрываем таблицу:
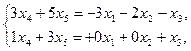
3) Применяем правило Крамера:
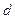 = 4;
= 4; 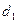 =
= 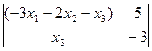 =
= 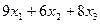 ;
; 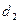 =
= 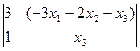 =
= 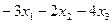 .
.
4). Общее решение системы: x 4 = 
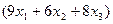 ; x 5 =
; x 5 = 
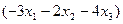 .
.
5). Построим ФСР (фундаментальную систему решений), избегая дробей:
| x 1 | x 2 | x 3 | x 4 | x 5 | |
| α 1 | -3 | ||||
| α 2 | -2 | ||||
| α 3 | -4 |
Векторы-решения 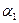 ,
, 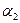 ,
, 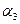 линейно независимы, их количество
линейно независимы, их количество 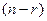 =3. Эти векторы могут быть приняты в качестве ФСР.
=3. Эти векторы могут быть приняты в качестве ФСР.
Ответ: общее решение: x 4 = 
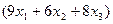 ; x 5 =
; x 5 = 
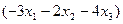 ;
;
ФСР: 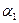 = (4, 0, 0, 9,–3);
= (4, 0, 0, 9,–3); 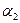 = (0, 4, 0, 6, –2);
= (0, 4, 0, 6, –2); 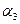 = (0, 0, 4, 8, –4).
= (0, 0, 4, 8, –4).
Пример 15 – 4: Найти общее решение системы уравнений: 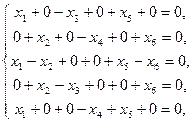 и фундаментальную систему решений.
и фундаментальную систему решений.
Решение:
1). Применим пошаговый процесс метода Гаусса:
| -1 | -1 | ||||||||||||
| -1 | -1 | ||||||||||||
| -1 | -1 | =(1)→ | -1 | -1 | =(2)→ | ||||||||
| -1 | -1 | ||||||||||||
| -1 | -1 |
| -1 | -1 | ||||||||||||
| -1 | -1 | ||||||||||||
| -1 | =(3)→ | -1 | =(4)→ | ||||||||||
| -1 | |||||||||||||
| -1 |
Выполнены операции: (1): [R3]–[R1]; [R5]–[R1]. (2): [R3]+[R2]; [R4]–[R2]. (3): [R4]+[R3]; [R5]–[R3]. (4): раскрываем полученный результат.
2). Видим: 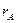 =3. Свободными неизвестными объявляем
=3. Свободными неизвестными объявляем  ,
, 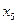 ,
,  .
.
|
|
|
3). Из уравнения [R3] следует: 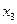 =
=  . Далее из уравнения [R2]:
. Далее из уравнения [R2]: 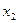 =
=  –
–  ; из уравнения [R1]:
; из уравнения [R1]: 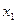 =
=  –
– 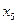 . Получено общее решение: как и в случае неоднородной системы уравнений.
. Получено общее решение: как и в случае неоднородной системы уравнений.
5). Построим ФСР (фундаментальную систему решений), избегая дробей:
| x 1 | x 2 | x 3 | x 4 | x 5 | x 6 | |
| α 1 | ||||||
| α 2 | -1 | |||||
| α 3 | -1 |
Векторы-решения 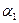 ,
, 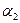 ,
, 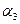 линейно независимы, их количество
линейно независимы, их количество 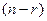 =3. Эти векторы могут быть приняты в качестве ФСР.
=3. Эти векторы могут быть приняты в качестве ФСР.
Ответ: общее решение 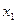 =
=  –
– 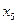 ,
, 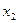 =
=  –
–  ;
; 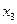 =
=  .
.
ФСР: 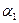 = (1,1,1,1,0,0);
= (1,1,1,1,0,0); 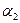 =(-1,0,0,0,1,0);
=(-1,0,0,0,1,0); 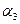 =(0,-1,0,0,0,1).
=(0,-1,0,0,0,1).
☻
Вопросы для самопроверки:
1. Можно ли, применяя метод Гаусса, провести полное исследование решений системы линейных уравнений с произвольным числом уравнений и неизвестных?
2. Можно ли решить систему уравнений методом Гаусса, если все значения свободных членов b i, i = 1, 2, …, n равны нулю?
3. Можно ли любую систему уравнений записать в виде матричного уравнения AX = B?
4. Можно ли, применяя правило Крамера, провести полное исследование решений системы линейных уравнений с произвольным числом уравнений и неизвестных?
5. Можно ли решить систему уравнений по правилу Крамера, если все значения свободных членов b i, i = 1,2, …, n равны нулю?
6. Как практически применяется теорема Кронекера-Капелли при решении системы линейных уравнений?
7. Можно ли провести полное исследование системы уравнений без использования теоремы Кронекера-Капелли?
8. Может ли ранг расширенной матрицы 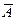 быть равным 7, а ранг А -матрицы 8? а наоборот?
быть равным 7, а ранг А -матрицы 8? а наоборот?
9. Могут ли ранги матриц А и 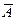 равняться нулю?
равняться нулю?
10. Является ли линейным векторным пространством множество всех решений однородной системы линейных уравнений с обычными операциями сложения и умножения на число?
11. Какова размерность линейного пространства решений однородной системы 8 линейных уравнений с 12 неизвестными, если ранг матрицы системы равен 4?
12. Что называется фундаментальной системой решений (ФСР) однородной системы линейных уравнений?
13. Как построить ФСР однородной системы линейных уравнений?
14. Сколько ФСР можно построить для заданной однородной системы линейных уравнений?
|
|
|
Задачи для самоподготовки:
Пример C15 – 1: Найти общее решение системы уравнений: 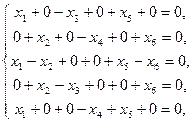 и фундаментальную систему решений.
и фундаментальную систему решений.
Ответ: общее решение x 1 = –6 x 3 + 5 x 4; x 2 = 8x 3 –7 x 4. ФСР: 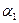 = (8, 6, 1, 0);
= (8, 6, 1, 0); 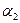 = (–7, 5, 0, 1).
= (–7, 5, 0, 1).
Пример C15 – 2: Найти общее решение системы уравнений:  и фундаментальную систему решений.
и фундаментальную систему решений.
Ответ: общее решение: 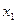 =
= 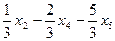 ,
, 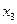 =
=  , или:
, или: 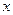 =
= 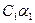 +
+ 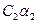 +
+ 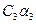 .
.
ФСР: 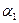 = (2, 0, 6, 0,0);
= (2, 0, 6, 0,0); 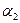 = (–4,–3, 0,6,0);
= (–4,–3, 0,6,0); 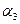 = (–10,9, 0, 0,6).
= (–10,9, 0, 0,6).
Пример C15 – 3: Найти общее решение системы уравнений: 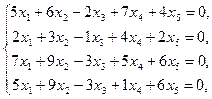 и фундаментальную систему решений.
и фундаментальную систему решений.
Ответ: общее решение: 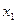 =0,
=0,  =0,
=0, 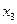 =
= 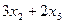 ; или:
; или: 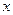 =
= 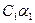 +
+ 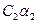 .
.
ФСР: 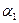 = (0,3,0,1,0);
= (0,3,0,1,0); 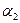 = (0,2,0,0,1).
= (0,2,0,0,1).
< * * * * * >
☺ ☻ ☺
Контрольная работа №2 предназначена оценить степень усвоения основных терминов, определений и свойств алгебраических конструкций, изучаемых «Линейной алгебре».
Состав и степень трудности предлагаемых в Контрольной работе заданий согласовывается с Методическим советом кафедры «Высшая математика».
При разработке заданий Контрольной работы учитывается также требование побудить студентов повторить пройденный материал по предмету. Это значит, что в заданиях не должно быть ничего такого, что, так или иначе, требует самостоятельных обобщений и выводов со стороны студентов.
Перед выполнением Контрольной работы студенты должны ознакомиться с перечнем вопросов, которые будут отражены в заданиях. Так же важным элементом подготовки к контрольной работе должны быть регулярные текущие контрольные мероприятия в виде оперативных опросов: по 6-7 минут в начале каждого занятия.
Прием части-2 БДЗ. Приём БДЗ определяется двумя последовательными мероприятиями:
1). Формальный приём выполненных Заданий непосредственно в аудитории: проверка на соответствие правилам закрепления вариантов заданий за каждым студентом.
2). Контроль выполненных Заданий преподавателем: проверка правильности решения заданий и соответствия требованиям по оформлению каждого задания БДЗ.
3). Защита выполненных заданий БДЗ каждым студентом в специально назначенное время (обычно, в день консультаций по предмету). Определение окончательной оценки качества выполнения Части-2 БДЗ.
Замечание: 1). Сборник заданий по БДЗ находится в информационной системе института с самого начала семестра, постоянно.
2). Сборник заданий по БДЗ содержит по каждому заданию примеры решения и оформления.
< * * * * * >
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 502; Нарушение авторских прав?; Мы поможем в написании вашей работы!