Дифференцирование на основе интерполяционной формулы Лагранжа

Дифференцирование на основе формулы Стирлинга

Формулы численного дифференцирования, рассмотренные ранее используют лишь значения функции при 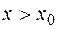. Более точный результат дают центральные формулы дифференцирования, которые учитывают значения данной функции как при 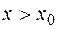, так и при . Одна из подобных формул получается, если взять за основу интерполяционную формулу Стирлинга.

Пусть - система равноотстоящих точек с шагом . Значения данной функции в этих точках 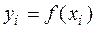. Заменив приближенно заданную функцию интерполяционным полиномом Стирлинга, получим:

Формула численного дифференцирования, основанная на формуле Стирлинга имеет вид

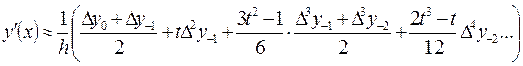
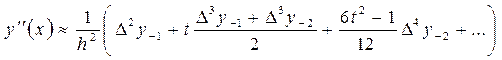
Пример. Вычислить значение первой и второй производных при 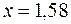. В таблице берем .

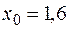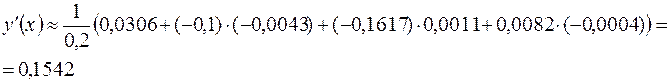
Пусть 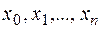равноотстоящие точки, , значения функции в этих точках известны и равны 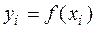. Таким образом, создана система равноотстоящих узловых точек, для которой можно построить многочлен Лагранжа

(1)

Значение полинома Лагранжа в точке 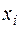совпадает со значением функции в этой точке

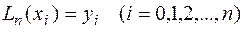(2)

Обозначим 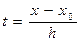, тогда

. (3)

Производная выражения (3) имеет вид

(4)

Подставив в (1) получим

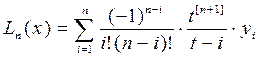(5)

Учитывая, что 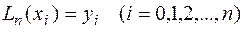найдем производную

,

Глава 5. Численное интегрирование функций

Если функция непрерывна на отрезке 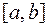и известна ее первообразная 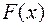, то определенный интеграл от этой функции на заданном отрезке вычисляется по формуле Ньютона – Лейбница .

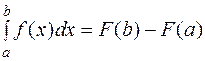Во многих случай первообразная функции не может быть найдена аналитически, либо является слишком сложной. На практике подынтегральная функция часто задается таблично и тогда само понятие первообразной не имеет смысла. Большое значение имеют приближенные и в первую очередь численные методы вычисления определенных интегралов. Задача численного интегрирования функции заключается в вычислении значения определенного интеграла на основании ряда значений подынтегральной функции. Численное вычисление однократного интеграла называется механической квадратурой, двойного – механической кубатурой. Соответствующие формулы называются квадратурными и кубатурными формулами. Метод состоит в том, что данную функцию на рассматриваемом отрезке 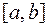заменяют интерполирующей или аппроксимирующей функцией 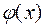простого вида (например, полиномом) и полагают

Функция 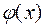должна быть такова, чтобы интеграл вычислялся непосредственно.

Дата добавления: 2014-12-27