Метод Эйлера. Простейшим одношаговым численным методом решения задачи Коши для обыкновенного дифференциального уравнения является метод Эйлера

Простейшим одношаговым численным методом решения задачи Коши для обыкновенного дифференциального уравнения является метод Эйлера. Метод основан на разложении искомой функции 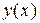в ряд Тейлора в окрестности точки 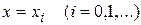, являющейся узлом сетки. В этом разложении отбрасываются члены, содержащие производные второго и более высоких порядков.

(3)

Заменим значения функции 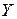в узлах 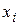значениями сеточной функции . 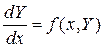, то значение первой производной в узлах сетки 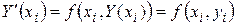. Допустим, узлы сетки являются равноотстоящими, т.е. . Шаг изменения аргумента 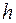определяется промежутком, в котором находится решение и количеством требуемых значений функции. Если X правая граница исследуемого промежутка значений аргумента, а n - количество значений функции, то шаг 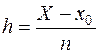. Если внутри отрезка функция сохраняет постоянное значение, то 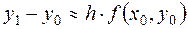, где - значение искомой функции в точке или 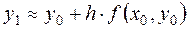. Повторяя этот алгоритма получим последовательные значения функции Соотношения имеют рекуррентный вид и представляют собой разностную схему метода Эйлера. Значения сеточной функции в любом узле вычисляются по значению в предыдущем узле. Метод Эйлера относится к одношаговым.

Интегральная кривая имеет вид ломаной линии с вершинами в точках .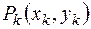

При решении задачи Коши методом Эйлера выбирается начальное приближение

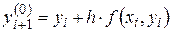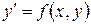, где , (4)

а затем это значение уточняется по формуле (5)

Пример. Решить задачу Коши для обыкновенного дифференциального уравнения первого порядка 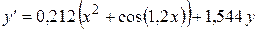на отрезке с шагом 0,1 при начальном условии .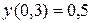

Вычисления проводить с четырьмя десятичными знаками.

Решение.

Используем для первичной оценки значения функции формулу

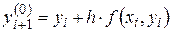, (6)

а для уточнения - формулу

. (7)

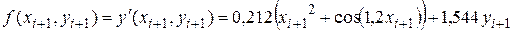, (8) (9)

Последовательность вычислений:

1. Подставив начальные значения 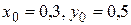в выражение (8), получим значение

и запишем его в столбец 4 таблицы.

2. Найдем грубую оценку и запишем в столбец 5.

3. Подставим значения 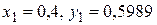в (9) получим

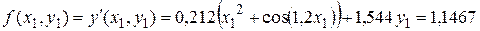, запишем в столбец 7.

4.Найдем точное значение 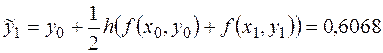и запишем в столбец 8.

5. Перезаписываем полученное значение в столбец 3 в строку, соответствующему следующему значению аргумента и теперь оно является исходным значение для расчета на следующем шаге.

6. Повторяем пп. 1-5 до полного заполнения таблицы.

Таблица 1

					оценка		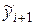Точное Значение
	0,3	0,5000	0,9895	0,0989	0,5989	1,1467	0,6068
	0,4	0,6068	1,1589	0,1159	0,7227	1,3438	0,7319
	0,5	0,7319	1,3581	0,1358	0,8678	1,5755	0,8786
	0,6	0,8786	1,5923	0,1592	1,0379	1,8478	1,0506
	0,7	1,0506	1,8676	0,1868	1,2374	2,1678	1,2524
	0,8	1,2524	2,1910	0,2191	1,4715	2,5436	1,4891
	0,9	1,4891	2,5709	0,2571	1,7462	2,9850	1,7669
		1,7669	3,0170	0,3017	2,0686	3,5031	2,0929
	1,1	2,0929	3,5406	0,3541	2,4470	4,1111	2,4755
	1,2	2,4755	4,1551	0,4155	2,8910	4,8243	2,9245
	1,3	2,9245

В результате расчета получим таблицу значений функции, удовлетворяющих исходному дифференциальному уравнению.

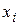
0,3	0,5000
0,4	0,6068
0,5	0,7319
0,6	0,8786
0,7	1,0506
0,8	1,2524
0,9	1,4891
	1,7669
1,1	2,0929
1,2	2,4755
1,3	2,9245

Существует модификация метода, которая называется методом Эйлера с уточнением и содержит вместо одного три приближения. Вычисления продолжаются до тех пор, пока два последовательных приближения не совпадут.

Пример. Используя метод Эйлера с уточнением, составить таблицу приближенных значений интеграла дифференциального уравнения , удовлетворяющего начальным условиям 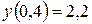на отрезке 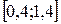. Значение шага взять равным 0,1. Все вычисления вести с четырьмя десятичными знаками.

Последовательность вычислений:

1. Значение производной в начальной точке (k=0)

записываем в (графу 4).

2. Вычисляем нулевое приближение для k =0:

и записываем в (графу 5).

3. Значение аргумента для k +1=1 .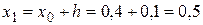

4. Первое уточнение для k =0

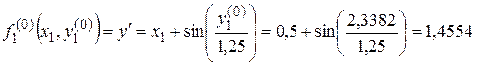(графа 6)

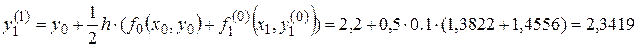(графа 7)

5. Второе уточнение

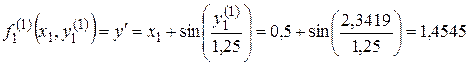(графа 8)

(графа 9)

6. Вычисляем производную, соответствующую полученному уточненному значению

(графа 10)

, следовательно, переходим к следующей итерации для k =1.

7. Приняв k =1 и повторяем вычисления в соответствии с пп 1-6.

Результаты вычислений представлены в таблице 2.

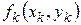
				yk +1^(0)		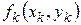yk +1^(1)	fk +1^(1)	yk +1^(2)	fk +1^(2)
	0,4	2,2000	1,3822	2,3382	1,4554	2,3419	1,4545	2,3418	1,4545
	0,5	2,3418	1,4545	2,4873	1,5135	2,4902	1,5125	2,4902	1,5125
	0,6	2,4902	1,5125	2,6414	1,5565	2,6436	1,5556	2,6436	1,5556
	0,7	2,6436	1,5556	2,7992	1,5847	2,8006	1,5840	2,8006	1,5840
	0,8	2,8006	1,5840	2,9590	1,5993	2,9597	1,5989	2,9597	1,5989
	0,9	2,9597	1,5989	3,1196	1,6019	3,1198	1,6018	3,1198	1,6018
		3,1198	1,6018	3,2799	1,5948	3,2796	1,5951	3,2796	1,5951
	1,1	3,2796	1,5951	3,4391	1,5805	3,4384	1,5810	3,4384	1,5810
	1,2	3,4384	1,5810	3,5965	1,5613	3,5955	1,5621	3,5956	1,5621
	1,3	3,5956	1,5621	3,7518	1,5397	3,7506	1,5406	3,7507	1,5406
	1,4	3,7507	1,5406

6.2. Метод Рунге – Кутта

Найти решение дифференциального уравнения 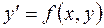при начальном условии 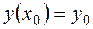в промежутке и заданном шаге h. При численном интегрировании уравнения методом Рунге – Кутта определяют четыре числа:

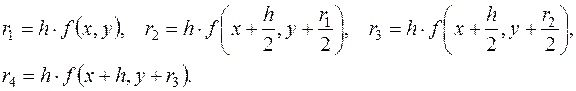
Значение искомой функции , где 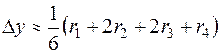. Схема вычислений имеет вид

x	y		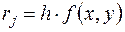Добавка

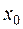
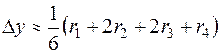
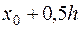
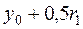
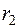
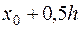
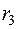
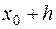
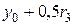
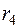
Дата добавления: 2014-12-27