Градиентные методы

Процесс оптимизации заключается в выборе наилучшего варианта из всех возможных. В процессе решения задачи оптимизации необходимо найти оптимальные значения параметров, определяющих данную задачу. Выбор оптимального решения проводится с помощью целевой функции, определяемой параметрами задачи.

Целевую функцию можно записать в виде

(1)

В результате оптимизации получают значения параметров, обеспечивающих минимум (или максимум) целевой функции. Допустим, имеется выпуклая целевая функция , которую необходимо минимизировать (максимизировать). Можно выделить два типа задач оптимизации:

1. Задачи без ограничений (задачи безусловной оптимизации), в которых необходимо отыскать абсолютный минимум (максимум) функции 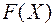от n действительных переменных и соответствующих значений аргументов на некотором множестве n -мерного пространства.

2. Задачи с ограничениями (задачи условной оптимизации) Ограничения задаются совокупностью некоторых функций, удовлетворяющих уравнениям или неравенствам. Ограничения можно записать в виде системы

(2)

Задача максимизации вогнутой функции 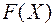эквивалентна задаче минимизации выпуклой функции - 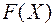, поэтому в дальнейшем рассмотрим методы решения задач минимизации выпуклой функции (задачи выпуклого программирования). Оптимальное решение может соответствовать либо локальному экстремуму (максимуму или минимуму) внутри области допустимых решений, либо значению целевой функции на границе области.

Общая схема широкого класса методов приближенного решения Алгоритм задачи безусловной минимизации следующий:

1. Выбор начального приближения.

2. Проверка условия оптимальности. Если оно выполняется, то работа алгоритма заканчивается, иначе – переходим к пункту 3.

3. Определение направления.

4. Определение шага.

5. Вычисление очередного приближения и переход к пункту 2 (проверка условия оптимальности.

Конкретные алгоритмы спуска отличаются правилами выбора направления и шага спуска. Градиентные методы используют для определения направления спуска производную целевой функции. Методы обладают х скоростью сходимости, но требуют довольно сложных вычислений.

7.2. Метод Франка – Вулфа

1. Определить исходное допустимое решение задачи .

2. Найти градиент функции в точке исходного допустимого решения .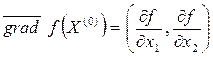

3. Построить линейную функцию

и найти оптимальное решение 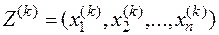, при котором ее значение максимально при заданных в задаче ограничениях.

4. Составить выражение для нового допустимого решения

,

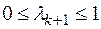
и подставить в целевую функцию задачи

5. Определить шаг вычислений как стационарную точку функции 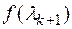из условия . Полученное значение 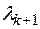есть шаг вычислений.

6. Вычислить новое допустимое решение

.

7. Вычислить значение .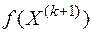

8. Проверить выполнение условия

.

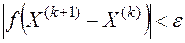Если оно выполняется, оптимальное решение найдено, если нет, то переходим к шагу 2.

Пример.

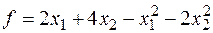
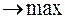
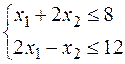
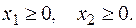
Решение.

1. Найдем градиент функции

.

2. В качестве исходного допустимого решения выберем точку , а в качестве критерия оценки качества получаемого решения неравенство 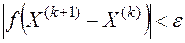, где .

1-я итерация

1. В точке найдем градиент функции , тогда необходимо решить задачу максимизации

при условии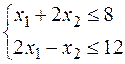

Решаем эту задачу симплекс – методом.

Каноническая задача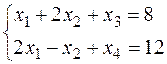

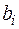
	базис						Q
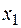
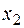
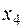
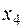
				-1			-----
			-2	-4
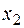
			1/2		1/2
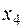
			5/2		1/2
							оптим

Оптимальное решение

2. Составим новое допустимое решение

,

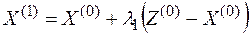Подставим в целевую функцию, получим

,

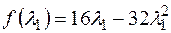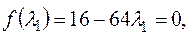
Тогда новое допустимое решение 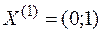, значение функции в этой точке .

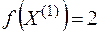3. 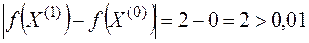, следовательно, переходим к следующей итерации.

2-ая итерация

1. В точке 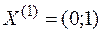найдем градиент функции , тогда необходимо решить задачу максимизации

при условии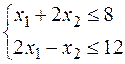

Решаем эту задачу симплекс – методом.

Каноническая задача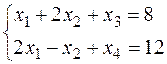

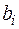
	базис						Q
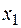
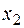
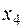
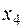
				-1
			-2
				5/2		-1/2
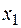
				-1/2		1/2
				-1
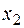
		4/5			2/5	-1/5
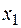
		32/5			1/5	2/5
		64/5			2/5	4/5	оптим

Оптимальное решение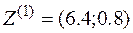

2. Составим новое допустимое решение

,

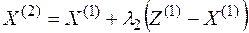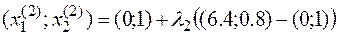
Подставим в целевую функцию, получим

,

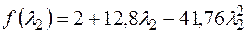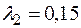
Тогда новое допустимое решение 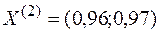, значение функции в этой точке .

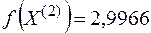3. , следовательно, переходим к следующей итерации.

3-я итерация

1. В точке 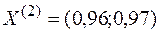найдем градиент функции 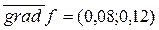, тогда необходимо решить задачу максимизации

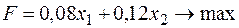при условии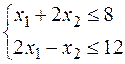

Решаем эту задачу симплекс – методом.

Каноническая задача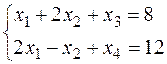

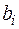
	базис		0,08	0,12			Q
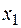
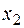
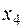
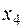
				-1			-----
			-0,08	-0,12
0,12		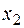	1/2		1/2
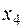
			5/2		1/2		32/5
		0,28	-0,02		0,06
0,12		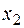4/5			2/5	-1/5
0,08		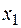32/5			1/5	2/5
		0,608			0,064	0,008	оптим

Оптимальное решение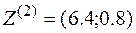

2. Составим новое допустимое решение

,

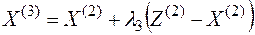Подставим в целевую функцию, получим

,

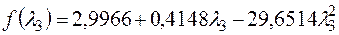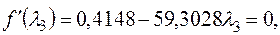
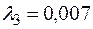
Тогда новое допустимое решение 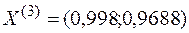, значение функции в этой точке .

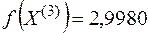3. 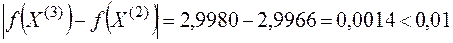, следовательно, вычисления закончены. Искомое решение .

Дата добавления: 2014-12-27