Тепловые схемы для конвективного теплообмена

Метод теплового баланса позволяет построить тепловые схемы для конвек­тивного теплообмена, возникающего при движении жидкости в канале или около поверхности тела, причем в этом случае необходимо введение новых схемных элементов, не используемых в тепловых схемах, моделирующих про­цессы теплопроводности, рассмотренные ранее.

Сначала рассмотрим метод для одномерной конвекции и затем для двумер­ного течения жидкости в плоскопараллельном канале.

Везде далее принимается, что жидкость несжимаема, теплофизические па­раметры жидкости постоянны. Течение считается гидродинамически стаби­лизированным, и вязкой диссипацией энергии пренебрегается.

3.3.1. Одномерное течение жидкости. Рассмотрим одномерное течение жидкости в прямом, направленном вдоль оси х канале, с известной темпера­турой стенки канала T_w = T_w(x,t) с площадью и периметром ее внутреннего сечения равными А, р, соответственно. Взаимодействие стенки канала и жид­кости характеризуется коэффициентом теплоотдачи 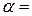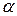(x,t). Плотность, удельную теплоемкость и теплопроводность жидкости обозначим как 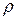, с, .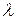

Дифференциальное уравнение баланса энергии имеет вид (см. п. 2.5.1 (2.54))

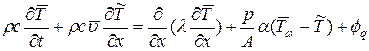
Выделим в жидкости произвольный объем V_i = 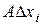, 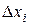= 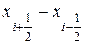, где 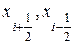- координаты границ объема вдоль оси х, ограниченного внутрен­ней поверхностью канала и двумя сечениями, перпендикулярными оси х.

Интегральное уравнение баланса теплоты для выделенного объема Vi имеет вид (см. (2.15))

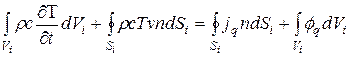(3.50)

q = - 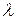gradT.

Введем среднемассовую температуру жидкости Т, среднюю по сечению ско­рость жидкости v и среднюю температуру жидкости Т равенствами (2.46) (2.48). Примем, что стенка канала имеет температуру большую чем темпе­ратура жидкости, что соответствует нагреву жидкости стенкой. Уравнение баланса (3.50) запишется в виде

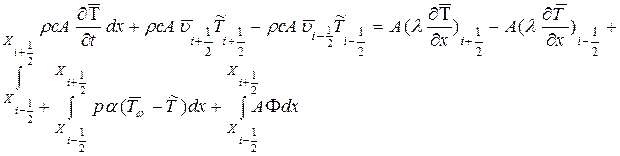
где Ф – средняя по сечению мощность внутреннего источника теплоты, равная

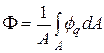
Расположим в центре каждого выделенного объема по одному узлу, при этом i-му объему соответствует узел с номером i. Тогда первый, предпоследний и последний члены в уравнении (3.51) можно приближенно записать через зна­чения входящих в них переменных в узле i (имеющим координату х =x_i), a именно

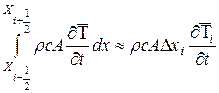
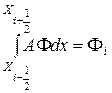
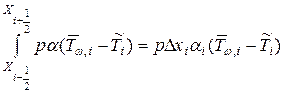(3.53)

Записав производные дТ/дх в уравнении (3.51) через конечные разности получим

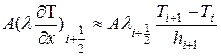
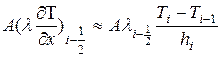(3.54)

а вводя тепловые сопротивления участков жидкости длиной h_i+1 и h_i;

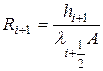
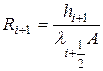(3.55)

вместо (3.54) получим

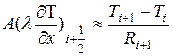(3.56)

Введя конвективное тепловое сопротивление R_aq = 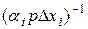соотношение (3.53) равно

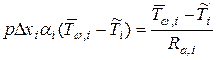(3.57)

С учетом соотношений (3.53), (3-56) и (3.57) интегральное уравнение баланса теплоты в выделенном объеме V; примет вид

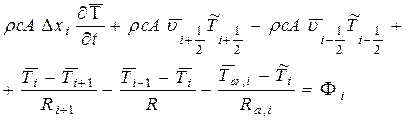(3.58)

В уравнение (3.58) входят две температуры, относящиеся к жидкости, а именно: 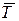и 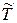. Будем считать их равными (подробнее об этом см. п. 2.5.1). Для упрощения записи далее примем следующие обозначения: 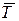= = 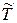Т, , .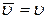

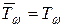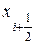Рассмотрим конвективные члены в уравнении (3.58), представленные вто­рым и третьим членами в его левой части. В эти члены входят скорости и температуры жидкости не в узлах, а на границах и выделенного объема. Поскольку поле скорости считается известным, то мы можем оста­вить их значения соответствующие координатам 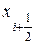и . Неизвестные же температуры жидкости, входящие в конвективные члены необходимо связать с температурами в узлах сетки. Для этого применим схему против потока, согласно которой значение температуры на грани конечного объема (в нашем случае выделенный объем V_i) принимается равным ее значению в соседнем узле со стороны, расположенной выше по течению потока, т.е. 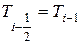a 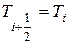при условии, что жидкость движется в положительном направлении оси х. Такое смещение значений температур жидкости с грани выделенного объема в ближайший узел, предшествующий этой грани, позволяет получать физически реальные результаты даже на грубой сетке, Таким образом, кон­вективные члены в уравнении (3.58) равны

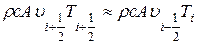
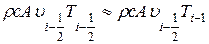(3.59)

Подставляя выражения (3.59) в уравнение (3.58) и учитывая сказанное выше получим

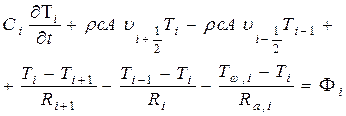3.60)

где Ci = pcA 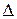x_i - полная теплоемкость выделенного объема V_i

.

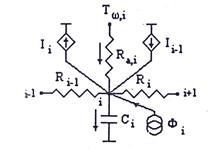(твердом теле), в тепловой схеме для движущейся жидкости появляются новые схемные элементы I_i-1=I_i-1(t) и I_i=I_i(t), представляющие собой нестационарные источники потока, управляемые соответствующими узловыми температурами и равные по величине

.

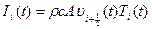Управляемые источники конвективных тепловых потоков I_i,i=1,2,…, независимы между собой. Поскольку величина 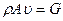, кг/с представляет собой массовый расход жидкости, протекающей через сечение площадью А в единицу времени, управляемый источник I_i может быть записан в ви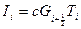де , где 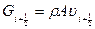- массовый расход жидкости в сечении . Отметим, что изменение во времени расхода жидкости по длине канала может происходить и за счет изменений площади сечения канала А, так что на правой, к примеру, границе 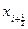i -го конечного объема V_i надо задавать площадь сечения 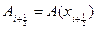, которая, в этом случае, может изменяться вдоль оси x, при этом расход жидкости будет равен 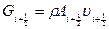. Все полученные соотношения и разностное уравнение (3.60) справедливы для переменной вдоль оси x площадь внутреннего сечения канала A(x), если функция A(x) является гладкой. При переменном сечении канала вдоль оси x кондуктивное и конвективное тепловые сопротивления жидкости определяется по формулам (см. п. 1.6)

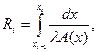
(3.61)

Где p(x) – переменный вдоль оси x периметр внутреннего сечения стенки канала; R_a,i = R_a,i(t) – конвективное тепловое сопротивление от стенки канала в жидкость.

Матричная запись. Запишем систему уравнений (3.60) в матричном виде. Здесь нас интересует структура матрицы, соответствующая конвективному теплообмену в жидкости, поэтому пренебрежем теплопроводностью жидкости вдоль оси x по сравнению с конвективным переносом. В этом случае уравнение энергии имеет вид

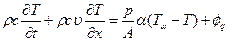
Температура жидкости на входе в канал известна и равна T_BX.

Разделим участок канала 0 < х < l на N конечных объемов и пронумеруем их так, что конечный объем с номером 1 является первым внутренним объемом после приграничного конечного объема с гранью, совпадающей с сечением ка­нала при x= 0. Во всех внутренних объемах узлы расположены в центре объема. Узел 0 в приграничном объеме V_о расположен на его левой грани при х = 0 и температура этого узла известна и равна T_вх.

Для всех внутренних объемов i = 2,..., N конечно-разностные уравнения, согласно (3.60), имеют вид

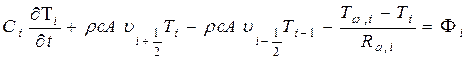
Поскольку температура узла 0 в приграничном объеме V_q известна и равна T_вх, то конечно-разностное уравнение для объема составлять не нужно.

Для первого конечного объема конечно-разностное уравнение имеет вид

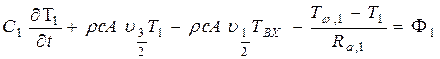
Система конечно-разностных уравнений может быть записана в матричном виде

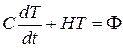
где Т= 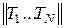- N - вектор-столбец неизвестных температур в N узлах сетки; Н - квадратная N xN -матрица, равная

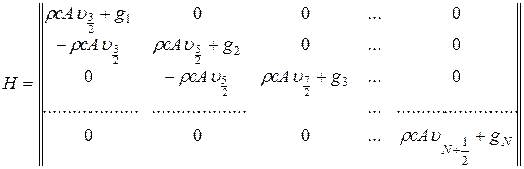
Ф - N- вектор-столбец с известными элементами, равный

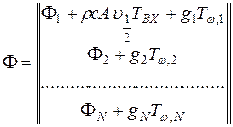
g_i = (R_iq)^-1 ~ тепловая проводимость взаимодействия стенки канала и жид­кости; С - диагональная N х N -матрица с элементами С₁,..., C_N по диаго­нали.

Вид матрицы H показывает, что она двухдиагональна и несимметрична; все ее элементы, кроме тех, что стоят на главной диагонали и нижней поддиагонали, равны нулю.

3.4. Двумерное течение жидкости.

Уравнения для внутренних узлов. Двумерное течение жидкости рас­смотрим на примере канала, образованного двумя плоскими, параллельными пластинами. Расстояние между пластинами равно 26, протяженность пласти­ны по оси х_з, перпендикулярной плоскости x₁x₂ - бесконечна. Будем рас­сматривать общий случай, когда скорость у может изменяться по осям xi и х₂ и зависит от времени t, т.е. v = v(x₁,x₂,t). Будем считать также, что в жидкости имеются внутренние источники теплоты. Изменение тем­пературы и скорости жидкости в направлении, перпендикулярном плоскости Xix₂ отсутствует. Течение жидкости в рассматриваемом случае - двумерно. Для простоты анализа будем пренебрегать теплопередачей теплопроводностью вдоль оси х₁ по сравнению с конвективным теплопереносом вдоль оси х₁, хотя это и не принципиально. При этих условиях поле температуры несжимаемой жидкости описывается интегральным уравнением баланса энергии в жидкости (см. п. 2.3.1 (2.15))

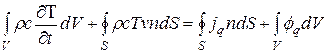(3.62)

справедливым для произвольного объема жидкости V, ограниченного поверх­ностью S, или равносильным ему дифференциальным уравнением (см. п. 2.3.2, (2.21))

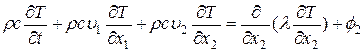(3.63)

В интегральном уравнении баланса (3.62) вектор скорости равен

v = v₁(x₁,x₂,t)i₁ +v₂{x_1tx₂,t)i₂, (3.64)

где i₁ и i₂ — единичные векторы вдоль осей x₁, x₂, вектор плотности теплового потока q направлен вдоль единичного вектора i₂ оси х₂, поскольку тепловой поток теплопроводности вдоль оси x₁, по принятому допущению, равен нулю.

Покроем плоскость х₁х₂ в области жидкости прямоугольной сеткой так, что область жидкости внутри канала будет разбита на элементарные прямоуголь­ные объемы с размерами вдоль осей х₁ и х₂ равным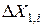и и 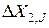; ^и единичной длины вдоль оси x_3. Площадь грани iq -ro объема V_iq=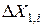 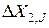x1, пер­пендикулярной оси x₁, обозначим A_iq = 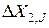x1, площадь грани, перпенди­кулярной оси x₂ обозначим A_2,i= 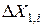x1. Координаты граней iq -ro объема будем обозначать как обычно: для граней, перпендикулярных оси х₁ как 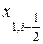и 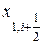; для граней, перпендикулярных оси х₂ как и 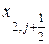центре каждого объема поместим по одному узлу. Применим уравнение баланса (3.62) к произвольному выделенному объему V_iq, окружающем узел iq. Первый член в левой части уравнения (3.62) равен

а последний член в правой части уравнения равен

Поскольку в рассматриваемом случае тепловой поток теплопроводности вдоль оси Xi не учитывается, поверхностный интеграл в правой части уравнения (3.62)

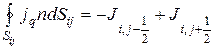(3.65)

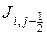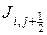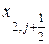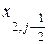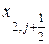Примем, что полные тепловые потоки и , пересекающие грани выделенного объема, имеющими координаты и соответственно определены в центрах этих граней по оси x₁, т.е. в месте расположения узла iq с координатой x_1,i по оси х₁. Тепловые потоки теплопроводности и равны

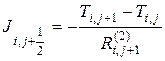(3.66)

Обратимся теперь к конвективному члену в уравнении (3.62). Имеем

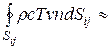
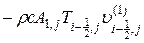
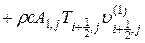
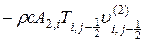
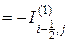
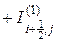
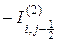
Конвективные тепловые поток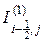и 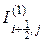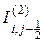и , и 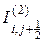необходимо связать с узловыми значениями температуры жидкости. Для этого исполь­зуем схему против потока, которая уже применялась в одномерном случае (см. п. 3.4.1).

Глава 4 Матрично-топологический метод анализа тепловых схем

В предыдущих разделах на основании общих уравнений баланса были получены разностные уравнения, являющиеся дискретным аналогом интегрального уравнения баланса потоков теплоты в произвольном выделенном конечном объеме. Процессы теплопередачи в теле или жидкости, разделенном на объемы, моделируются системой обыкновенных дифференциальных уравнений относительно неизвестных температур в узлах сетки. Было показано также, что эта же система уравнений описывает распределение тепловых потоков в ветвях и температур в узлах соответствующей тепловой схемы.

Тепловая схема, моделирующая процессы теплопередачи в теле или жидкости строится на основе физического понимания протекающих процессов, не прибегая к явной записи конечно-разностных уравнений. Тепловая схема имеет прозрачный физический смысл и ее построение, основанное на конкретных правилах, значительно проще получения системы конечно-разностных уравнений. Система конечно-разностных уравнений относительно неизвестных температур в узлах тепловой схемы, получается благодаря использованию матрично-топологических методов. Эти методы позволяют формализовано записывать искомые уравнения и, тем самым, открывает путь к автоматизации формирования уравнений с помощью ЭВМ, что особенно важно для сложных технических объектов, приводящих к системам уравнений большой размерности.

Ниже излагается матрично-топологический метод, применение которого к тепловой схеме позволяет сразу получить конечно-разностные уравнения баланса в матричной форме относительно узловых температур.

Собственно методом тепловых схем будем называть совокупность двух методов: метода построения тепловой схемы и матрично-топологического метода составления уравнений схемы для последующего их решения.

Дата добавления: 2014-12-27