Матрично-топологические соотношения в тепловой схеме

В предыдущих разделах было установлено, что процессы теплопереноса в некотором объекте (жидкости или твердом теле) могут моделироваться с помощью тепловой схемы, состоящей из узлов, соединенных между собой ветвями. Ветви тепловой схемы содержат элементы одного из следующих типов: тепловые сопротивления, тепловые емкости, источники тепловых потоков, источники заданных температур, управляемые источники тепловых потоков, конвективные ветви, представляющие собой последовательно соединенные конвективное тепловое сопротивление и источник заданной температуры среды. Совокупность узлов и ветвей, с теми или иными элементами, будем называть графом тепловой схемы, причем свойства графа будем рассматривать безотносительно к типу элементов, представленных ветвями графа. Если в каждой ветви задано определенное направление, граф становится ориентированным. Соединение ветвей графа с узлами образуют структуру тепловой схемы и отражают ее типологию, т.е. взаимное расположение узлов и ветвей тепловой схемы и связи между ними.

Независимо от типа элементов а ветвях тепловой схемы каждая ветвь характеризуется направлением теплового потока в ней и температурами узлов, которые она соединяет. Направление теплового потока в ветви указывает на то, что узел, из которого тепловой поток вытекает, имеет более высокую температуру, чем узел, в который этот тепловой поток втекает. Поскольку температуры узлов в тепловой схеме до ее расчета неизвестны, направления ветвей графа, за исключением ветвей с источниками тепловых потоков, источниками заданных температур и управляемыми источниками потоков, полностью произвольны. Для источников теплового потока, направление протекающего теплового потока задано. Для конвективной ветви, содержащей конвективное тепловое сопротивление и источник с заданной температурой среды, направление теплового потока в ветви зависит от того, нагревается объект средой или охлаждается ею. Если объект охлаждается, т.е. происходит теплообмен со средой, имеющей температуру меньшую, чем температура объекта, тепловой поток в ветви направлен от узла, связанного с объектом, к узлу с известной температурой среды. В противном случае, т.е. при нагреве тела более горячей средой, направление теплового потока в конвективной ветви – противоположно. Ветви графа, соответствующие различным элементам тепловой схемы, с положительным направлением теплового потока в них, показаны на рис. 4.1. Узел с нулевой температурой (ноль по Цельсию илипо Кельвину), относительно которой отсчитываются температуры в остальных узлах тепловой схемы, графически обозначается значком .

Матрица AGA^T в точности идентична матрице Н (см. п. 3.1.5), если принять во внимание, что g₁ и g_n+1 в разностной схеме (п. 3.1.5) равны g_,i0 и g_a,_l на тепловой схеме. Вектор Q+AGT_a равен

Q + AGTa =

имеет размерность п и полностью идентичен вектору Ф(t) всистеме разностных уравнений (см. п. 3.1.5). На этом примере показана идентичность уравнений, получаемых методом теплового баланса и матрично-топологическим методом.

4.2.2. Тепловые схемы, моделирующие теплообмен в движущейся жидкости. Особенностью тепловых схем, моделирующих конвективный те­плообмен в движущейся жидкости, по сравнению с тепловыми схемами, мо­делирующими теплоперенос в неподвижных твердых телах, рассмотренными выше, является наличие в них управляемых источников тепловых потоков. Управляемые источники тепловых потоков моделируют конвективные члены в уравнении энергии движущейся жидкости.

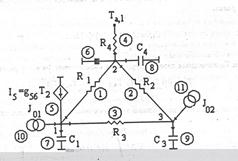
Рис. 4.5. Произвольная тепловая схема с управляемым источником теплового потока I5. Номера ветвей показаны в кружках.

Рассмотрим произвольную тепловую схему (рис. 4.5). Схема состоит из трех узлов и одного нулевого узла, соответствующего нулевой температуре. С каждым узлом соединены ветви, содержащие тепловые емкости. К узлу 2 под­соединена ветвь с источником известной температуры T_a,1, к узлам 1 и 3 под­соединены независимые источники тепловых потоков Q₀₁ и Q₀₂ соответственно. Новым является включение ветви 5 с управляемым источником теплового по­тока, величина которого равна I₅ = g₅₆T₂ где g₅₆ управляющий коэффициент, Т₂ - температура второго узла.

Получим уравнения, описывающие нестационарное распределение темпера­тур в узлах тепловой схемы.

Для записи потока управляемого источника с помощью матрично-топологи­ческого метода введем фиктивную ветвь 6, подключенную к узлу 2, темпера­тура которого управляет зависимым источником теплового потока /5. Фиктив­ная ветвь 6 имеет нулевую проводимость и на тепловой схеме выглядит так, как показано на рис. 4.5. Очевидно, что разность температуры ∆Т₆ в фик­тивной ветви 6 равна температуре Т₂. Введение фиктивной ветви с нулевой проводимостью облегчает применение матрично-топологического метода при составлении уравнений и не влияет на перераспределение тепловых потоков в схеме и вид конечной системы уравнений, поскольку проводимость фиктивной ветви равна нулю.

Пронумеруем в произвольном порядке узлы схемы (за исключением нуле­вого узла). Сгруппируем ветви схемы следующим образом: сначала нумеруем ветви с кондуктивными и конвективными тепловыми проводимостями, затем нумеруем ветви с управляемыми источниками тепловых потоков и фиктивные ветви, затем ветви с тепловыми емкостями и, наконец, ветви с независимыми источниками тепловых потоков. С учетом сказанного относительно нумерации узлов и ветвей, матрица инциденций равна

Представим матрицу инциденций А в блочном виде

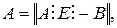
где

.

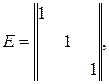
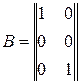Матрица А является матрицей инциденций для тепловой схемы, из которой исключены ветви с тепловыми емкостями и независимыми источниками те­пловых потоков.

В соответствии с классификацией ветвей в матрице инциденций А, запи­шем вектор-столбец тепловых потоков ветвей I = || i₁i_2…i₁₁ || ^T, где i₁, i₂, i₃ - тепловые потоки в ветвях с тепловыми проводимостями, ц - тепловой поток в ветви с независимым источником температуры, i₅ =I₅=g₅₆T₂ - тепловой поток управляемого источника теплового потока, i₆ - тепловой поток в фиктив­ной ветви (очевидно, что i₆ = 0), i₇ = C₁dT₁/dt, i₈ = C₂dT₂/dt, i₉ = C₃dT₃/dt - тепловые потоки в ветвях с тепловыми емкостями, i₁₀=I₀₁, i₁₁=I₀₂ - тепловые потоки независимых источников. Вектор-столбец I представим в блочном виде, а именно, I = || I₁ I₂ I₃ || ^T, где I₁ = || i₁ i₂…i₆ || ^T, I₂ = || i₇ i₈ i₉ || ^T, I₃ = || Q₀₁ Q₀₂ || ^T.

Матрично-топологическое соотношение AI = 0 (4.3), с учетом блочного представления матрицы А и вектора-столбца I имеет вид

AI₁ + I₂ - BI₃ = 0,

где

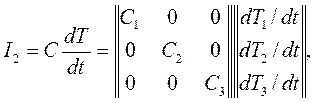(4.18)

T = ║T₁ T₂ T₃║^T - вектор-столбец неизвестных узловых температур; В1₃ = ║Q₀₁ 0 Q₀₂ ║^T -вектор-столбец известных тепловых потоков независимых ис­точников тепловых потоков.

Вектор-столбец I₁, как это следует из рис. 4,5, связан с разностями темпе­ратур ∆Ti, i= 1,2,..., 6 в ветвях тепловой схемы следующим соотношением

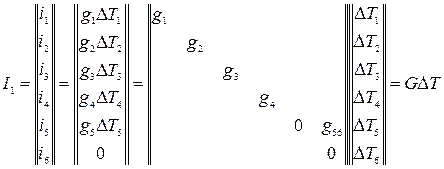, (4.19)

а вектор-столбец разностей температур ∆T = ║∆T₁ ∆T₂ ∆T₃║^Т связан с температурами в узлах соотношениями

, (4.20)

где Т_а = ||0 0 0 T_a,1 0 0|| ^T - вектор-столбец известных температур независимых источников температуры. Подставляя (4.20) в (4.19) получим

I₁=GA^TT-GT_a, (4.21)

а подставив (4.21) в (4.17) и учитывая конкретный вид векторов-столбцов I₂ и BIз, получим, окончательно, нестационарное матрично-топологическое уравнение, описывающее искомый вектор температур в узлах тепловой схемы

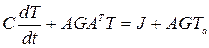. (4.22)

Уравнения (4.16) и (4.22) совпадают по виду, хотя и описывают различные тепловые схемы. Различие в уравнениях состоит только в матрице тепловых проводимостей G. Алгоритм получения матричного уравнения (4.22) подобен алгоритму_} приведенному в п. 4.2.1 с некоторой модификацией, обусловленной наличием в тепловой схеме управляемых источников тепловых потоков.

Алгоритм состоит из следующих шагов:

1. Ввести в тепловую схему фиктивные ветви с нулевой проводимостью, ко­торые подключаются между нулевым узлом и теми узлами, температуры кото­рых управляют зависимыми источниками тепловых потоков, расположенных в других ветвях. Количество фиктивных ветвей равно количеству управляющих температур в зависимых источниках тепловых потоков.

2. Пронумеровать в произвольном порядке узлы схемы, присвоив нулевой номер узлу с нулевой температурой. В конвективных ветвях узлы между те­пловой проводимостью и независимым источником заданной температуры не нумеруются.

3. Пронумеровать в произвольном порядке ветви тепловой схемы в том числе и фиктивные. Нумеровать следует только ветви, содержащие тепловые прово­димости, управляемые источники тепловых потоков и фиктивные ветви. На­помним, что ветвь с последовательно соединенной тепловой проводимостью и независимым источником заданной температуры рассматривается как единая ветвь (конвективная ветвь).

4. Составить матрицу инциденций А, как это описано в алгоритме в п. 4.2.1.

5. Составить матрицу тепловых проводимостей G, размерность которой равна М × М, где М - количество пронумерованных ветвей. Нумерация строк идет сверху вниз, а столбцов слева направо. Если ветвь i содержит тепловую проводимость g_i,- или последовательно включенный независимый источник за­данной температуры и тепловую проводимость g_i, то диагональный элемент ii матрицы G равен g_i; если ветвь i содержит управляемый источник тепло­вого потока равный I_i = giqT_q где T_q - температура q -гo узла, то элемент iq матрицы G равен giq; если ветвь i является фиктивной, то диагональный элемент ii матрицы G равен нулю.

6. Шаги 6, 7, 8, которые относятся к составлению матрицы тепловых ем­костей С, векторов-столбцов независимых источников тепловых потоков Q и независимых источников заданных температур Т_а, ничем не отличаются от соответствующих шагов алгоритма, изложенного в п. 4.2.1.

4.3. О численном решении уравнений. Выше были установлены уравнения, описывающие процессы теплопередачи, протекающие в различного рода объектах, которые моделируются тепловыми схемами. Эти уравнения представляют собой систему обыкновенных диффе­ренциальных уравнений относительно вектора неизвестных нестационарных температур Т = T(t) в узлах тепловой схемы и, в матричной форме, имеют

вид

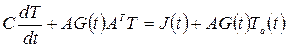(4.23)

с начальным условием

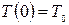, (4.24)

где А - N×M - матрица инциденций, N - число узлов (кроме нулевого узла), М - число ветвей, содержащих тепловые проводимости, управляемые источники тепловых потоков и ветви с нулевыми проводимостями (в случае конвектив­ного теплообмена); G - М×М -матрица тепловых проводимостей; матрица G диагональна, когда рассматривается неподвижная жидкость или твердое тело; Q – N - вектор-столбец независимых источников тепловых потоков; Т_а – М - вектор-столбец известных температур независимых источников температур; С - N×N - диагональная матрица тепловых емкостей; Т₀= ║ T_1,0…T_N,0 ║ ^T вектор-столбец начальных температур в момент времени t = 0 в N узлах тепловой схемы.

Все матрицы, входящие в систему (4.23) известны, матрица G в общем слу­чае может зависеть от времени.

В стационарном случае, вектор-столбец температур Т описывается матрич­ным уравнением, получающимся из (4.23) при dT/dt = 0, т.е.

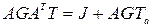. (4.25)

Матричное уравнение (4.25) представляет собой систему линейных алгебраи­ческих уравнений.

Не останавливаясь на описании численных методов решения уравнений вида (4.23) и (4.25)¹ отметим, тем не менее, особенности применения численных методов к рассматриваемым системам уравнений.

Как уже было показано, системы уравнений вида (4.23) и (4.25) описывают процессы теплопередачи в тепловых схемах, моделирующих как сложные объ­екты, так и конвективный теплообмен в движущейся жидкости. Если рас­сматривается теплопередача в твердом объекте с теплообменом со средой по ли­нейному закону Ньютона, матрица G является диагональной. Если рассматри­вается теплообмен в движущейся жидкости, матрица G - не диагональна. Раз­личие в структуре матрицы G обусловливает и различие в методах, которые необходимо применять при решении систем уравнений.

Рассмотрим сначала уравнения, описывающие теплопередачу в объекте, с поверхностей которого происходит теплообмен со средой, при этом, теплообмен собственно в жидкости не рассматривается. В этом случае, как уже было сказано, матрица тепловых проводимостей G является диагональной и N × N- матрица системы уравнений H = AGA^T обладает рядом полезных свойств:

1. Матрица системы Н=AGA^T является симметрической. Это следует из очевидных равенств Н^T = (AGA^T)^T = AGA^T = H.

2. Матрица Н = AGA^T является положительно определенной. Напомним, что симметрическая матрица H называется положительно определенной, если квадратичная форма

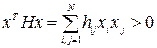
для всех ненулевых векторов х, где h_tq - элементы матрицы Н; x_i - элементы вектора х.

Покажем, что матрица H = AGA^T - положительно определенная. Заметим сначала, что диагональная матрица G (ее элементы g_iq, являющиеся тепло­выми проводимостями, всегда положительны; среди элементов g_iq могут быть нулевые) положительно определенная, что следует из соотношения

т.к. g_iq > 0. Для любого вектора х имеем х^TНх = x^TAGA^Tx = у^TGy > 0, где у = А^Tх, а неравенство - есть следствие положительной определенности матрицы G и того факта, что ранг N×М - матрицы равен N. Таким образом, N×M - матрица H = AGA^T является положительно определенной.

Симметрическая, положительно определенная матрица системы H=AGA^T обладает следующими свойствами², которые приводим без доказательства:

1. Каждое собственное значение положительно определенной матрицы по­ложительно и действительно.

2. Определитель матрицы H положителен.

3. Матрица Н может быть представлена в виде произведения H=LU, где L и U - треугольные матрицы (нижняя и верхняя соответственно), причем это разложение будет единственным, если заранее зафиксировать диагональ­ные элементы одной из треугольных матриц (например, положить их равными единице). Матрица H может быть представлена также в виде H = LL^T.

Второе свойство гарантирует невырожденность матрицы H и тем самым гарантирует существование решения.

Третье свойство позволяет применить к решению стационарной системы уравнений (4.25) такие эффективные численные точные методы, как метод ква­дратных корней, метод Холецкого, метод Гаусса и их разновидности. Все эти методы основаны на разложении матрицы в произведение двух треугольных (нижней и верхней) матриц. Элементы матриц L и U определяются по рекурентным формулам. Имея разложение H = LU, решение системы уравнений НТ = F, где F = Q+AGT₀ - известный вектор-столбец, разделяется на два эта­па: на первом этапе, который называют прямым ходом, определяется вектор у из системы уравнений Ly = F, на втором этапе, называемым обратным ходом, определяется искомый вектор Т из системы уравнений UT = у. Поскольку матрицы L и U треугольные, системы уравнений относительно векторов y и Т легко решаются с помощью рекурентных формул.

Для решения стационарной системы уравнений НТ=F c положительно определенной матрицей H можно построить сходящиеся и эффективные ите­рационные процессы. Они существенно опираются на положительную опре­деленность матрицы Я, поскольку в этом случае система всегда может быть подготовлена к виду, в котором метод итерации сходится³.

Рассмотрим решение нестационарного матричного уравнения

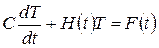(4.26)

H(t) = AG(t)A^T, F(t) = Q(t) + AG(t)T_a(t),

с начальным условием

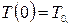(4.27)

где H(t) - положительно определенная матрица для всех t ≥ 0.

Наиболее распространенными методами решения нестационарного матрич­ного уравнения (4.26) с начальным условием (4.27) являются явный и неявный методы Эйлера. Явный метод Эйлера приводит к итерационной процедуре

(4.28)

а неявный метод Эйлера - к итерационной процедуре

(4.29)

где m - номер итерации, h - шаг по времени; Е - диагональная единичная матрица; T_m=T(t_m), Н_т = H(t_m), F_m = F(t_m), t_m = t₀ + mh, m = 0,1,2,... - значения соответствующих вектор-столбцов и матриц в момент времени t_m.

В явном методе Эйлера значение вектора-столбца температуры Т_т в следую­щий момент времени t_m находится пересчетом по формуле (4.28) на основании известного значения температуры Т_т-1 в предыдущий момент времени t_m-1. В неявном методе Эйлера для определения температуры T_m+1 в момент вре­мени t _m+1 необходимо решать систему линейных алгебраических уравнений (4.29), с известной правой частью в предыдущий момент времени t_m.

Процесс итерации для уравнения (4.28) будет устойчивым, если все собст­венные значения λ_i,- матрицы Е – hC^-1 Hm удовлетворяют условию | λ_i | < 1, i — 1,2,..., N. Можно показать, что это условие равносильно выполнению двух условий относительно собственных значений μ матрицы С^-1Нт и шага h по времени:

μ; >0, (4.30)

Поскольку матрица Н_т положительно определена, а все элементы диагональ­ной матрицы положительны, за исключением некоторых элементов, равных нулю, собственные значения матрицы С^-1 Нт положительны (см. свойство 1), т.е. условия μ_i > 0, i = 1,2,..., N. выполнены. Второе условие (4.30) ограни­чивает максимальный допустимый шаг по времени h. Это условие довольно жесткое, так как приходится выбирать мелкий шаг h, что приводит к увели­чению затрат машинного времени и, в ряде случаев, к результатам с большой погрешностью.

Для устойчивого решения системы (4.29) необходимо, чтобы собственные значения λ _i; матрицы Е + hC^-1H_m+1 удовлетворяли условию | λ_i| > 1, i = 1,2,..., N или равносильному условию

(4.31)

которое выполняется для любых h > 0, поскольку собственные значения μ_i матрицы C^-1 H_m+1 положительны. Следовательно, при неявном методе Эйлера решение всегда устойчиво и максимальное значение шага ограничивается только требуемой точностью решения.

В случае теплообмена в движущейся жидкости матрица Н = AGA^T, как уже отмечалось, не является симметрической, поскольку матрица G недиагональна. Но и в этом случае, матрица G содержит только положительные элементы и некоторое количество нулевых.

При составлении системы уравнений (4.23) или (4.25) матрично-топологическим методом, получающиеся уравнения являются линейно независимыми и количество неизвестных N равно количеству полученных уравнений. Поэтому матрица Н= AGA^T имеет ранг N и, следовательно, является невырожденной, а система уравнений имеет единственное нетривиальное решение.

Для решения стационарного матричного уравнения (4.25) с несимметричной матрицей Н = AGA^T применимы известные численные методы, например, метод Гаусса, метод Холецкого и т.д. и различные итерационные процедуры.

Методы решения матричного нестационарного дифференциального уравне­ния в обыкновенных производных (4.23) с несимметрической матрицей Н = AGA^T можно найти в уже упомянутой литературе⁴.

Дата добавления: 2014-12-27