Правила вычисления двойных интегралов 2 страница

Функцию 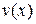выберем так, чтобы выражение в скобках обращалось в ноль:

.

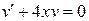Получили ДУ с разделяющимися переменными. Находим 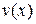как частное решение этого ДУ:

,

.

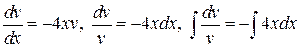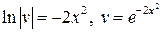Для определения 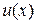также получаем ДУ с разделяющимися переменными:

,

,

.

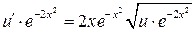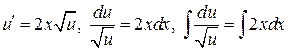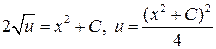Тогда – общее решение исходного уравнения.

5.3. Дифференциальные уравнения второго порядка,

допускающие понижение порядка

ДУ второго порядка может быть задано в

– общем виде:

;

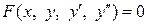– разрешенном относительно старшей производной виде:

.

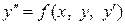Задача Коши для ДУ второго порядка имеет вид

, ,

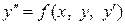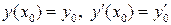т. е. в точке задаются значения искомой функции 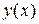и ее производной .

Общее решение ДУ второго порядка имеет вид 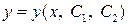, т. е. зависит от двух произвольных постоянных. Один из основных методов решения произвольных ДУ второго порядка – понижение порядка уравнения.

Рассмотрим некоторые типы ДУ второго порядка, допускающие понижение порядка.

1. . Общее решение находят двухкратным интегрированием:

,

.

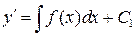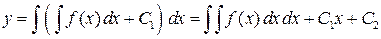2. 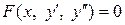, т.е. ДУ не содержит искомой функции у. Подстановкой 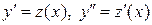исходное ДУ сводится к ДУ первого порядка относительно новой неизвестной функции .

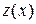3. 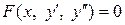, т. е. ДУ не содержит независимой переменной x. Подстановкой 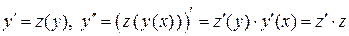исходное ДУ сводится к ДУ первого порядка относительно новой неизвестной функции .

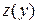Пример 5.4. Решить ДУ второго порядка, используя методы понижения порядка:

.

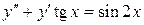Это уравнение вида 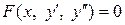, т.е. не содержит у. Используем подстановку 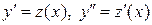. Получаем ДУ первого порядка относительно неизвестной функции :

.

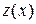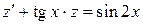Это линейное ДУ. Используем подстановку :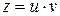

.

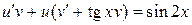Функцию 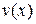находим как частное решение ДУ:

,

.

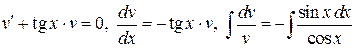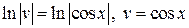Функцию 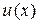находим как общее решение ДУ:

.

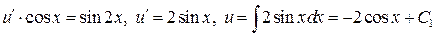Тогда

.

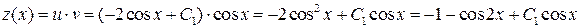Возвращаемся к исходным переменным:

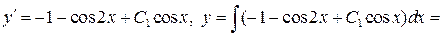
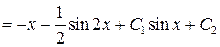– общее решение исходного уравнения.

Пример 5.5. Решить ДУ второго порядка, используя методы понижения порядка:

.

Это уравнение вида 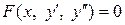, т. е. не содержит х. Используем подстановку .

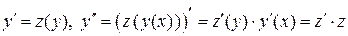Подставляя выражения для 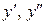в исходное ДУ, получим ДУ первого порядка, где у становится независимой переменной, 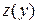– неизвестной функцией:

.

Разделяем переменные и интегрируем:

.

Так как 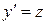, то , 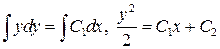– общий интеграл исходного ДУ.

5.4. Линейные дифференциальные уравнения второго порядка

ДУ имеют вид

.

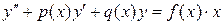Если 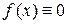, то ДУ принимает вид

и называется линейным однородным ДУ (ЛОДУ). Если 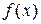T 0, то уравнение называется линейным неоднородным ДУ (ЛНДУ). Если 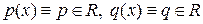, то уравнение называют линейным ДУ с постоянными коэффициентами.

Рассмотрим ЛОДУ с постоянными коэффициентами

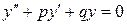
Для нахождения его общего решения составляют характеристическое уравнение

.

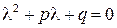При решении этого квадратного уравнения возможны три случая

1. 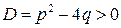. Уравнение имеет два действительных различных корня (кратность каждого корня 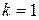). Тогда общее решение исходного ЛОДУ имеет вид

.

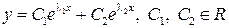2. 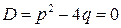. Уравнение имеет два равных корня 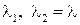(говорят, что корень 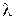имеет кратность ). Тогда общее решение исходного ЛОДУ имеет вид

.

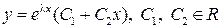3. 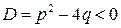. Уравнение имеет два комплексно сопряженных корня 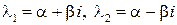(кратность каждого корня 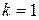). Тогда общее решение исходного ЛОДУ имеет вид

.

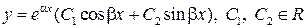Рассмотрим далее ЛНДУ с постоянными коэффициентами

.

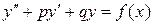Его общее решение задается формулой

,

где 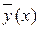– общее решение соответствующего ЛОДУ ;

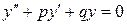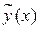– любое частное решение данного ЛНДУ.

Рассмотрим частный случай, когда правая часть ЛНДУ 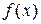является функцией специального вида

,

где 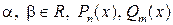– многочлены от х степеней n, m соответственно. Решение в этом случае проводят по следующей схеме.

1. Составляют характеристическое уравнение соответствующего ЛОДУ и находят его корни. Выписывают общее решение соответствующего ЛОДУ .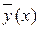

2. По виду правой части 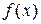выписывают число 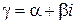. Если 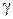не является корнем характеристического уравнения соответствующего ЛОДУ, то частное решение ЛНДУ 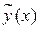ищут в виде

,

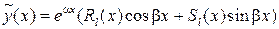а если 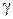является корнем кратности 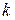, то в виде

,

где 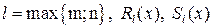– многочлены от х степени l c неопределенными коэффициентами.

Подставляя выражение для 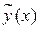в исходное ЛНДУ, вычисляют значения неопределенных коэффициентов многочленов и выписывают частное решение ЛНДУ .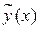

3. Общее решение исходного ЛНДУ находят в виде .

Пример 5.6. Найти частное решение ДУ, удовлетворяющее заданным начальным условиям

.

Решение. Это ЛНДУ второго порядка с постоянными коэффициентами и правой частью специального вида. Для соответствующего ЛОДУ 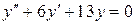составляем характеристическое уравнение:

, ,

.

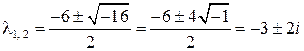Общее решение ЛОДУ имеет вид

.

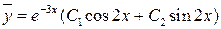По виду правой части ЛНДУ выписываем число 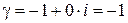. Оно не является корнем характеристического уравнения ЛОДУ, поэтому частное решение ЛНДУ 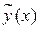ищем виде 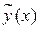= . Вычисляем производные:

= ;

;

.

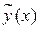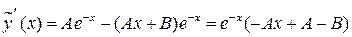Подставляем в ЛНДУ:

.

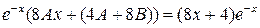Приравнивая коэффициенты при одинаковых степенях х в левой и правой части равенства, получаем:

,

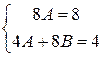откуда .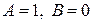

Подставляя найденные значения А, В в 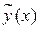, имеем 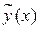= . Итак, 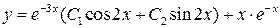– общее решение исходного ДУ.

Найдем частное решение, удовлетворяющее заданным начальным условиям. Вычисляем

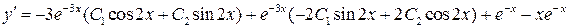
и подставляем начальные условия в :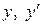

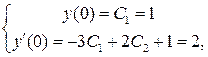
откуда .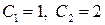

Подставляя 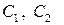в общее решение у, получаем искомое частное решение

.

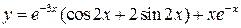Задание 6

Найти общее решение или общий интеграл дифференциального уравнения.

6.1. 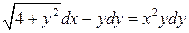. 6.2. .

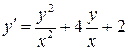6.3. . 6.4. .

6.5. . 6.6.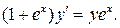

6.7. 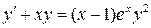. 6.8. .

6.9. . 6.10. .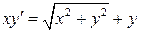

6.11. . 6.12. .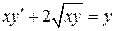

6.13. 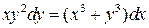. 6.14. .

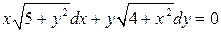6.15. 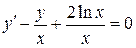. 6.16. .

6.17. . 6.18. .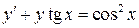

6.19. . 6.20. .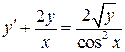

6.21. 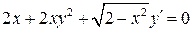. 6.22. .

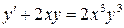6.23. 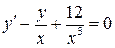. 6.24. .

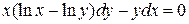6.25. 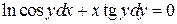. 6.26. .

6.27. 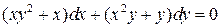. 6.28. .

6.29. 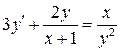. 6.30. .

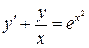Задание 7

Решить дифференциальное уравнение второго порядка, используя методы понижения порядка.

7.1. 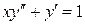. 7.2. .

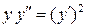7.3. . 7.4. .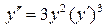

7.5. 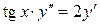. 7.6. .

7.7. 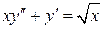. 7.8. .

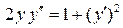7.9. 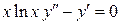. 7.10. .

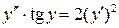7.11. . 7.12. .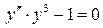

7.13. 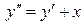. 7.14. .

7.15. . 7.16. .

7.17. . 7.18. .

7.19. 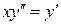. 7.20. .

7.21. . 7.22. .

7.23. 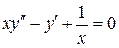. 7.24. .

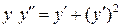7.25. . 7.26. .

7.27. . 7.28. .

7.29. 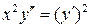. 7.30. .

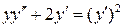Задание 8

Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.

8.1. .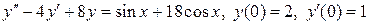

8.2. .

8.3. .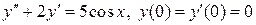

8.4. .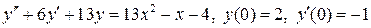

8.5. .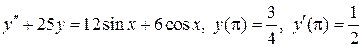

8.6. .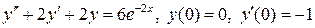

8.7. .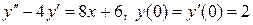

8.8. .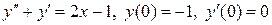

8.9. .

8.10. .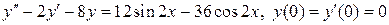

8.11. .

8.12. .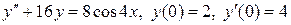

8.13. .

8.14. .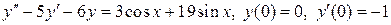

8.15. .

8.16. .

8.17. .

8.18. .

8.19. .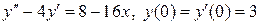

8.20. .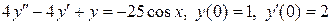

8.21. .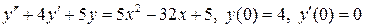

8.22. .

8.23. .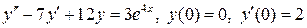

8.24. .

8.25. .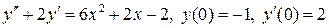

8.26. .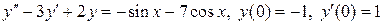

8.27. .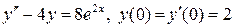

8.28. .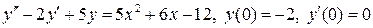

8.29. .

8.30. .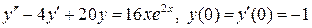

Тема 6. РЯДЫ

1. Числовые ряды. Сумма ряда. Действия над сходящимися рядами. Необходимый признак сходимости.

2. Знакоположительные ряды. Достаточные признаки сходимости.

3. Знакопеременные ряды. Абсолютная и условная сходимость.

4. Знакочередующиеся ряды. Признак Лейбница.

5. Степенные ряды. Теорема Абеля. Радиус и интервал сходимости степенного ряда.

6.1. Числовые ряды. Необходимый признак сходимости

Пусть дана числовая последовательность 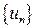. Числовым рядом называется выражение вида

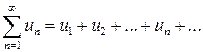
Числа 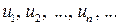называют членами ряда, 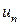– общий член ряда.

Сумму первых членов ряда называют – ой частичной суммой ряда и обозначают

.

Если существует конечный предел 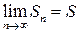, то ряд называют сходящимся, а число называют его суммой. Если последовательность 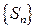не имеет конечного предела при , то говорят что ряд расходится.

Необходимый признак сходимости. Если ряд 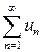сходится, то .

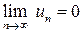Следствие (достаточное условие расходимости). Если 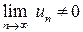или не существует, то ряд 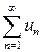расходится.

Пример 6.1. Исследовать на сходимость ряды.

а) .

Дата добавления: 2014-12-27