
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Отношения. Множество всех подмножеств множества М называется булеаном и обозначается 2M:
|
|
|
|
Алгебра подмножеств
Множество всех подмножеств множества М называется булеаном и обозначается 2 M:
2 м = { А | А 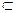 М }.
М }.
ТЕОРЕМА Для конечного множества М
|2 М | = 2| М |.
Свойства операций над множествами
Пусть задан универсум U. Тогда 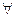 А, В, С
А, В, С 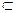 U выполняются следующие свойства.
U выполняются следующие свойства.
1. идемпотентность:
A 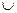 A=A A
A=A A 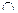 A=A;
A=A;
2. коммутативность:
A 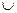 B= B
B= B 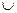 A A
A A 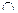 B= B
B= B 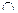 A;
A;
3. ассоциативность:
A 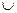 (B
(B 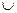 C) = (A
C) = (A 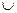 B)
B) 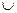 C, A
C, A 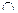 (B
(B 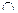 C) = (A
C) = (A 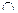 B)
B) 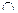 C;
C;
4. дистрибутивность:
A 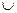 (B
(B 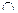 C) = (A
C) = (A 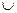 B)
B) 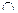 (A
(A 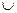 C), A
C), A 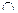 (B
(B 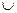 C) = (A
C) = (A 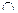 B)
B) 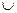 (A
(A 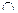 C);
C);
5. поглощение:
(A 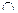 B)
B) 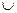 A=A (A
A=A (A 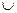 B)
B) 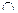 A=A;
A=A;
6. свойства нуля:
A 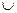 Æ =A, A
Æ =A, A 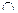 Æ = Æ;
Æ = Æ;
7. свойства единицы:
A 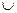 U=U, A
U=U, A 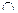 U=A;
U=A;
8. инволютивность:
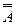 = A;
= A;
9. законы де Моргана:


10. свойства дополнения:
A 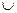
 =U A
=U A 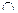
 = Æ;
= Æ;
11. выражения для разности:
A\B=A 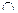
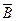 .
.
Упорядоченные пары
Если а и b — объекты, то через (а, b)обозначим упорядоченную пару. Равенство упорядоченных пар определяется следующим образом:
(а, b) = (с, d) Û а = c & b = d.
Вообще говоря, (а, b) ¹ (b, а).
Замечание
Упорядоченные пары можно рассматривать как множества, если определить их так:
(а, b) = { а, { а, b }}.
Таким образом, понятие упорядоченной пары не выводит рассмотрение за пределы теории множеств, но независимое определение технически удобнее.
Прямое произведение множеств
Пусть A и B — два множества. Прямым (декартовым) произведением двух множеств А и В называется множество упорядоченных пар, в котором первый элемент каждой пары принадлежит А, а второй принадлежит В:
А ´ В = {(а, b) | а 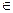 А & b
А & b 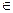 В }.
В }.
Степенью множества А называется его прямое произведение самого на себя. Обозначение:
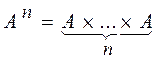
Соответственно, А 1 = А, А 2= А ´ А и вообще Аn = А ´ A n -1
ТЕОРЕМА | А ´ В | = | А | | В |.
СЛЕДСТВИЕ |Ап| = |А|п.
Отношения
Пусть А и В — два множества. (Бинарным) отношением (или предикатом) R из множества А в множество В называется подмножество прямого произведения А и В:
|
|
|
R 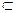 А ´ B.
А ´ B.
Для бинарных отношений обычно используется инфиксная форма записи:
аRb = (a, b) 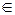
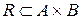
Если А = В, то говорят, что R есть отношение на множестве А.
Пример
Пусть задан универсум U. Тогда 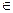 (принадлежность) — отношение из множества U в множество 2 U,а
(принадлежность) — отношение из множества U в множество 2 U,а 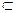 (включение) и = (равенство) — отношения на 2 U. Хорошо известны отношения =, <, <, >, >,
(включение) и = (равенство) — отношения на 2 U. Хорошо известны отношения =, <, <, >, >, 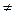 , определенные на множестве чисел.
, определенные на множестве чисел.
Пусть R есть отношение на A: R 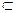 А ´ A, a, b
А ´ A, a, b 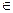 А. Введем следующие понятия
А. Введем следующие понятия
Обратное отношение: R -1 = {(а, b) | (b, а) 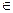 R }.
R }.
Дополнение отношения:  ={(а, b) | (a, b)
={(а, b) | (a, b) 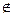 R }.
R }.
Тождественное отношение: I = {(а, а) | а 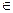 А }.
А }.
Универсальное отношение: U = {(а, b) | а 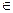 А & b
А & b 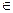 А }.
А }.
Введем обобщенное понятие отношения: n-местное (n-арное)отношение R -это множество упорядоченных наборов (кортежей):
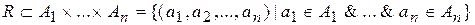
Множества Ai не обязательно различны.
Свойства отношений
Пусть R Ì А2. Тогда отношение R называется
рефлексивным, если " а Î A aRa;
антирефлексивным, если " а Î A Ø аRа;
симметричным, если " а,b Î A aRb 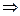 bRa;
bRa;
антисимметричным, если " а,b Î A aRb& bRa 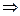 a = b;
a = b;
транзитивным, если " а,b Î A aRb & bRc 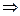 aRc;
aRc;
полным, или линейным, если " а,b Î A a ¹ b 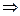 аRb Ú bRа.
аRb Ú bRа.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 976; Нарушение авторских прав?; Мы поможем в написании вашей работы!