
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Операции над графами
Рассмотрим операции над графами.
I. Бинарные операции.
1. Объединение графов. Рассмотрим графы 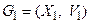 и
и 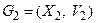 . Объединение графов
. Объединение графов  и
и  , обозначаемое как
, обозначаемое как  , представляет собой такой граф
, представляет собой такой граф 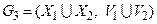 , что множество его вершин является объединением
, что множество его вершин является объединением  и
и  , а множество ребер – объединением
, а множество ребер – объединением 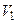 и
и  .
.
2. Пересечение графов. Пересечение графов  и
и  , обозначаемое как
, обозначаемое как 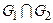 , представляет собой граф
, представляет собой граф  . Таким образом, множество вершин графа
. Таким образом, множество вершин графа 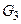 состоит только из вершин, присутствующих одновременно в графах
состоит только из вершин, присутствующих одновременно в графах  и
и  , а множество ребер графа
, а множество ребер графа 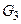 состоит только из ребер, присутствующих одновременно в графах
состоит только из ребер, присутствующих одновременно в графах  и
и  .
.
3. Кольцевой суммой  графов G1 и G2 называется граф
графов G1 и G2 называется граф 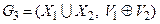 , где
, где 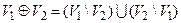 .
.
Замечание. Объединение, пересечение и другие операции над ориентированными графами определяются точно также, как и в случае неориентированных графов.
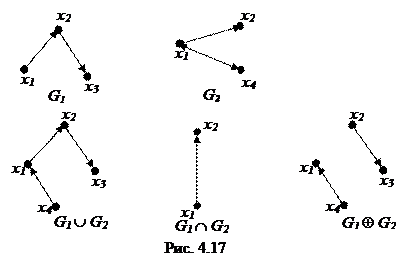
Пример. Для графов найдем G1 =({ x 1, x 2, x 3}, {(x 1, x 2), (x 2, x 3)}) и G2 =({ x 1, x 2, x 4}, {(x 1, x 2), (x 4, x 1)}) (рис. 4.17) найдем  ,
, 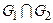 ,
,  . По определению имеем
. По определению имеем
 =({ x 1, x 2, x 3, x 4},{(x 1, x 2), (x 2, x 3),(x 4, x 1)}),
=({ x 1, x 2, x 3, x 4},{(x 1, x 2), (x 2, x 3),(x 4, x 1)}),
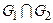 =({ x 1, x 2}, {(x 1, x 2)}),
=({ x 1, x 2}, {(x 1, x 2)}),
 =({ x 1, x 2, x 3, x 4}, {(x 2, x 3), (x 4, x 1)}).
=({ x 1, x 2, x 3, x 4}, {(x 2, x 3), (x 4, x 1)}).
4. Соединением графов G1 + G2 называется граф 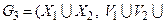 {(xi, xj) | xi Î X 1, xj Î X 2, xi ¹ xj }).
{(xi, xj) | xi Î X 1, xj Î X 2, xi ¹ xj }).
Пример. Для графов G1 и G2, показанных на рис. 4.18 а, соединением G1+G2 является граф, представленным на рис. 4.18 б.
5. Произведением  графов G 1 и G 2 называется граф
графов G 1 и G 2 называется граф  , в котором ((x 1, y 1), (x 2, y 2))Î V тогда и только тогда, когда x 1= x 2 и (y 1, y 2)Î V 2, или y 1= y 2 и (x 1, x 2)Î V 1.
, в котором ((x 1, y 1), (x 2, y 2))Î V тогда и только тогда, когда x 1= x 2 и (y 1, y 2)Î V 2, или y 1= y 2 и (x 1, x 2)Î V 1.
 |
Пример. На рис. 4.19 изображено произведение
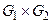 графов G 1=({1, 2}, {(1, 1), (2, 1)}) и G 2 = ({ a, b, c },{(a, b), (b, a), (b, c)}).
графов G 1=({1, 2}, {(1, 1), (2, 1)}) и G 2 = ({ a, b, c },{(a, b), (b, a), (b, c)}).
 |
II. Унарные операции.
1. Удаление вершины. При удалении вершины из графа удаляются и все инцидентные ей ребра (дуги).Пусть 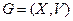 – граф и
– граф и 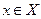 . Удалить вершину x из графа G – это значит построить новый граф
. Удалить вершину x из графа G – это значит построить новый граф  , в котором
, в котором 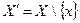 и
и  получается из V удалением всех ребер, инцидентных вершине x. Вот иллюстрация удаления вершины x из графа:
получается из V удалением всех ребер, инцидентных вершине x. Вот иллюстрация удаления вершины x из графа:
 |
До удаления вершины x После удаления вершины x
 |
2. Удаление ребра (дуги). Пусть
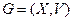 – граф и
– граф и  . Удалить ребро (дугу) v – это значит построить новый граф
. Удалить ребро (дугу) v – это значит построить новый граф  , в котором
, в котором  и
и 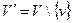 . Вот иллюстрация удаления ребра графа:
. Вот иллюстрация удаления ребра графа:
До удаления ребра v. Послеудаления ребра v
При удалении ребра (дуги) его концевые вершины не удаляются. Операцией, являющейся обратной к удалению ребра, является добавление ребра.
3. Слияние или отождествление вершин. Говорят, что вершины  и
и  в графе G отождествляются (сливаются), если они заменяются такой новой вершиной
в графе G отождествляются (сливаются), если они заменяются такой новой вершиной  , что все ребра (дуги) графа, инцидентные
, что все ребра (дуги) графа, инцидентные  и
и  , становятся инцидентными новой вершине
, становятся инцидентными новой вершине  .
.
4. Стягивание ребра (дуги). Эта операция означает удаление ребра и отождествление его концевых вершин. Граф G 1 называется стягиваемым к графу G 2, если граф G 2 может быть получен из G 1 в результате некоторой последовательности стягиваний ребер.
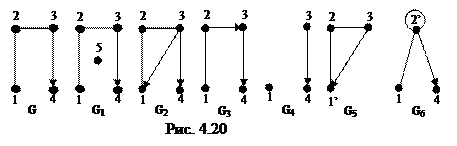 Пример. Из графа G, показанного на рис. 4.20, добавлением вершины 5 образуется граф G1, добавлением дуги (3,1) – граф G2, удалением дуги (3,2) – граф G3, удалением вершины 2 – граф G4, отождествлением вершин 1 и 4 – граф G5, стягиванием дуги (2,3) – граф G6.
Пример. Из графа G, показанного на рис. 4.20, добавлением вершины 5 образуется граф G1, добавлением дуги (3,1) – граф G2, удалением дуги (3,2) – граф G3, удалением вершины 2 – граф G4, отождествлением вершин 1 и 4 – граф G5, стягиванием дуги (2,3) – граф G6.
5. Подразбиение ребра. Пусть 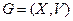 – граф и
– граф и 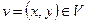 . Выполнить подразбиение ребра v – это значит построить новый граф
. Выполнить подразбиение ребра v – это значит построить новый граф  , в котором
, в котором 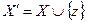 (т.е. z – некая новая вершина) и
(т.е. z – некая новая вершина) и 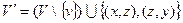 . С графической точки зрения эта операция означает «внесение в ребро новой вершины». Вот графическая иллюстрация:
. С графической точки зрения эта операция означает «внесение в ребро новой вершины». Вот графическая иллюстрация:
 xx
xx
z
yy
До внесения вершины z После внесения вершины z
Граф  называется дополнением простого графа, если ребро (xi, xj) входит в
называется дополнением простого графа, если ребро (xi, xj) входит в 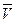 в том и только в том случае, если она не входит в V. Другими словами, две вершины смежны в
в том и только в том случае, если она не входит в V. Другими словами, две вершины смежны в  тогда и только тогда, когда они не смежны в G.
тогда и только тогда, когда они не смежны в G.
Пусть G’ =(X’, V’) является подграфом графа G =(X, V). Подграф G’’ =(X, V \ V’) графа G называется дополнением графа G’ в графе G.
|
|
Дата добавления: 2014-12-27; Просмотров: 3089; Нарушение авторских прав?; Мы поможем в написании вашей работы!