Основные определения. Деревья, остовы и кодеревья

Деревья, остовы и кодеревья

Понятие дерева как математического объекта было впервые предложено Кирхгофом в связи с определением фундаментальных циклов, применяемых при анализе электрических цепей. Деревья имеют особое положение в теории графов из-за предельной простоты строения, и часто при решении какой-либо задачи на графах ее сначала исследуют на деревьях.

Важность деревьев определяется широким приложением в различных областях знания. Понятие дерева применяется при конструировании различных алгоритмов (определение базисных циклов, базисных разрезающих множеств, проверка графа на двудольность и другие). Кратчайшее остовное дерево находит применение при решении задач, в которых необходимо связать n точек некоторой сетью так, чтобы общая длина «линий связи» была минимальной (прокладка дорог, газопроводов, линий электропередачи).

Деревом называется конечный связный граф без циклов, имеющий не менее двух вершин.

Если G – граф с n вершинами, то остовным деревом (остовом) графа G называется всякий остовный подграф графа G, являющийся деревом.

Пример. G – граф, показанный на рис. 4.29(а), то граф 4.29(б) является остовом графа G, как и граф, изображённый на рис. 4.29(в). Из сформулированных выше определений вытекает, что остов графа G можно также рассматривать как минимальный связанный остовный подграф графа G. Вообще говоря, остов определяется неоднозначно.

а б в

Рис.4.29 Граф G и его остовы: а – граф G, б – остов графа G, в – другой остов

K-деревом называется ациклический граф, состоящий из k компонент связности.

Если k -дерево является остовным подграфом графа G, то оно называется k - остовом графа G.

Кодерево Т* остова Т графа G – это остовный подграф графа G, содержащий только те ребра G, которых нет в Т. Ребра остова Т называются ветвями, а ребра соответствующего кодерева Т * – хордами.

Лесом L графа G называется остовное k -дерево графа G, где k - число компонент связности в G. Любой неорграф без циклов называется ациклическим гра­фом или лесом. Таким образом, компонентами связности любого леса являются деревья. На рис. 4.30 изображен лес, состоящий из двух деревьев.

Теорема 4.11.1. Для неориентированного графа G без петель содержащего n вершин характеристические свойства дерева эквивалентны:

1) G связен и не содержит циклов;

2) G не содержит циклов и имеет (n -1) ребро;

3) G связен и имеет (n -1) ребро;

4) G не содержит циклов, но добавление ребра между любыми двумя несмежными вершинами приводит к появлению цикла;

5) G связен, но утрачивает это свойство после удаления любого ребра;

6) Всякая пара вершин соединена цепью и притом только одной.

Из теоремы 4.11.1 вытекает следствие.

Следствие 4.11.1. Число ребер произвольного неорграфа G, которые необходимо удалить для получения остова, не зависит от последовательности их удаления и равно m–n + k, где m – число ребер, n – число вершин, k – число компонент связности графа G.

Доказательство. Действительно, если i-я компонента связности С_i графа G содержит n_i вершин, то по теореме 4.11.1. соответствующее дерево К_i остова содержит n_i– 1 ребро. Следовательно, для получения К_i из компоненты С_i нужно уда­лить m_i – (n_i – 1) ребер, где m_i – число ребер в C_i. Сумми­руя удаляемые ребра по всем компонентам связности и замечая, что 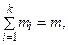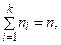получаем, что необходимо удалить ребер.

Число n(G) = m – п + k называется цикломатическим чис­лом или циклическим рангом графа G. Число v*(G)– п – k называется коциклическим рангом или корангом. Таким обра­зом, v*(G) есть число ребер, входящих в любой остов графа G, и v(G)+v*(G)=m.

Очевидны следующие два следствия.

Следствие 4.11.2. Неорграф G является лесом тогда и толь­ко тогда, когда, v(G) = 0.

Следствие 4.11.3. Неорграф G имеет единственный цикл, то­гда и только тогда, когда v(G)= 1.

Введем определение ориентированного дерева. Ориентированное дерево (древовидность) представляет собой орграф без контуров, в котором полустепень захода каждой вершины, за исключением одной (например, r), равна 1, а полустепень захода вершины r равна 0. Вершина r называется корнем дерева.

На рис. 4.31 показан граф, который является ориентированным деревом с корнем в вершине x ₁. Из приведенного определения следует, что ориентированное дерево с n вершинами содержит n – 1 дугу и связно.

Рис. 4.31. Ориентированное дерево

Следует отметить, что неориентированное дерево можно преображать в ориентированное: надо взять его произвольную вершину в качестве корня и ребрам приписать такую ориентацию, чтобы каждая вершина соединялась с корнем (только одной) простой цепью. Обратно, если T =(X, V) – ориентированное дерево, то T = (X, V), где V – множество дуг дерева Т без учета их ориентации, является неориентированным деревом.

Рассмотрим два остовных дерева T ₁=(X,A₁) и Т₂ =(Х,А₂) графа G. Преобразование дерева T₁ в дерево Т₂ называется элементарным преобразованием дерева, если дерево Т₂ можно получить из дерева T₁, удалив из T₁ дугу (ребро) а₁ и добавив дугу (ребро) a₂ (a₁ Î А₁, a₂ Î A₂). В этом случае считают что расстояние между T₁ и Т₂ d (Т₁,Т₂)=1. Если T₂ можно получить из T₁ с помощью k элементарных преобразований, то d (T₁,T₂)= k.

Граф остовов графа G – это граф, полученный следующим образом: каждому остову графа G сопоставим определенную вершину, а две вершины в новом графе соединяются ребром тогда и только тогда, когда расстояние между соответствующими им остовами равно 1.

Кратчайший остов графа G – это остов, у которого сумма весов ребер наименьшая.

Дата добавления: 2014-12-27