Анализ нормального распределения

Наиболее информативное использование средней арифметической и стандартного отклонения дает анализ больших выборок, когда данные отражаются в виде кривой, близкой к нормальному распределению[28].

Рассмотрим гипотетический пример. Пусть речь идет о выборке из 1000 семей и нас интересует, сколько денег выделяют родители подросткам на карманные расходы в день[29].

Снова обратимся для определения средней арифметической к знакомой формуле:

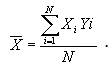
Для определения средней арифметической строим табл. 14.2.

Средняя арифметическая сумма денег, выделяемая подросткам на карманные расходы у нас получилась равной 62,6 (62635: 1000). Чтобы упростить дальнейшие действия, приравняем полученное среднее арифметическое к 62,5 руб., которое соответствует максимальному количеству случаев – 120.

Таблица 14.2

Денежные средства, выделяемые родителями подросткам на карманные расходы

№	Карманные деньги на один день, интервал в руб.	Средняя величина интервала, Х i	Количество случаев, Y i	Х i х Y i
	10-15	12,5
	15-20	17,5
	20-25	22,5
	25-30	27,5
	30-35	32,5
	35-40	37,5
	40-45	42,5		2507,5
	45-50	47,5		3847,5
	50-55	52,5		5197,5
	55-60	57,5
	60-65	62,5
	65-70	67,5
	70-75	72,5
	75-80	77,5
	80-85	82,5		4867,5
	85-90	87,5
	90-95	92,5
	95-100	97,5		1462,5
	100-105	102,5		922,5
	105-110	107,5		537,5
	110-115	112,5		112,5
			S = 1000	S = 62635

Далее строим соответствующую кривую (см. рис. 14.3).

Мы видим, что кривая симметрична и более или менее соответствует нормальному распределению, которое, между прочим, обладает определенными свойствами.

Но сначала выясним, чему равно в нашем случае стандартное отклонение.

Рис. 14.3.

Кривая распределения денежных сумм, выделяемых

подросткам на карманные расходы

Снова обращаемся к соответствующей формуле:

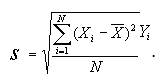
Для определения стандартного отклонения строим табл. 14.3.

Таблица 14.3

Определение стандартного отклонения

№	Х i, средняя величина интервала	Х i – 62,5	(Х i – 62,5)^2	Y i, количество случаев	(Х i – 62,5)^2 х Y i
	12,5	–50
	17,5	–45
	22,5	–40
	27,5	–35
	32,5	–30
	37,5	–25
	42,5	–20
	47,5	–15
	52,5	–10
	57,5	–5
	62,5
	67,5
	72,5
	77,5
	82,5
	87,5
	92,5
	97,5
	102,5
	107,5
	112,5
				S = 1000	S = 267605

Делим сумму квадратов разностей между средней величиной интервала и средней арифметической – на общее количество случаев: 267605: 1000 = 267,605. ______

Определяем квадратное отклонение: √267,605 = 16,359. Округляем до 16,4.

Из того факта, что кривая близка к нормальному распределению, вытекают следующие ее свойства: 68,3% всех случаев должно лежать в пределах одного стандартного отклонения в обе стороны от среднего арифметического, 95,5% – в пределах двух стандартных отклонений в обе стороны, и 99,7% всех случаев должны находиться в пределах трех стандартных отклонений в обе стороны от среднего арифметического.

При средней арифметической 62,5 и стандартном отклонении 16,4 соответствующие границы будут равны 78,9 и 46,1 (62,5±16,4), 95,3 и 29,7 (62,5±32,8), 111,7 и 13,3 (62,5±49,2).

На рис. 13.3 прерывистыми вертикальными линиями показаны границы соответствующих стандартных отклонений в обе стороны.

Эти границы означают следующее.

Допустим, мы хотим узнать, с какой вероятностью мы встретимся с подростком, родители которого выдают на карманные расходы сумму в пределах от 46,1 до 62,5 рублей в день. Мы находим соответствующие точки на кривой и выясняем, что они располагаются между серединой кривой и пересечением кривой с левой границей одного стандартного отклонения, это значит, что вероятность встречи с таким подростком равна 34,15% (68,3: 2). Можно сказать, опираясь на эти данные, что примерно каждый третий подросток получает на карманные расходы в пределах от 46,1 до 62,5 рублей в день. И соответственно, каждый третий получает от 62,5 до 78,9 рублей в день, если учитывать пересечение кривой с правой границей одного стандартного отклонения.

А вот вероятность встречи с подростком, получающим на карманные расходы от 29,7 до 46,1 рублей в день равна 13,6% (95,5: 2 – 68,3: 2).

Но нас может заинтересовать вероятность встречи с подростком, получающим на карманные расходы в диапазоне от 95,3 до 111,7 рублей в день. Эта вероятность равна всего 2,1% (99,7: 2 – 95,5: 2).

А вот вероятность встретиться с подростком, получающим от родителей на карманные расходы сумму от 13,3 до 111,7 рублей, равна 99,7%.

Можно определить вероятность встречи с подростком, карманные расходы которого лежат в диапазонах, не совпадающих точно с границами, заданными стандартными отклонениями. Но для этого нужны расчеты, основанные на теории вероятности, и мы не будем в это углубляться.

Отметим одну особенность кривой нормального распределения. Допустим, что мы уже построили такую кривую на основе выборки, достаточной большой, чтобы начали действовать законы больших чисел[30]. Разделим любою половину кривой – от середины до крайней точки – на три части. И в результате получаем без долгих вычислений приблизительную величину стандартного отклонения.

Например, в случае нашей кривой расстояние от крайней левой точки до максимума равно 50 (62,5 – 12,5). Делим это число на 3, получаем 16,66… Это близко полученному ранее стандартному отклонению 16,4.

Введем теперь так называемую стандартную оценку. Она определяет, насколько далеко находится определенная точка на кривой от средней арифметической. Формула стандартной оценки:

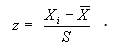
Здесь X i – точка на абсциссе, 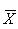– среднее арифметическое, s – стандартное отклонение.

Стандартная оценка позволяет сравнивать степень удаленности интересующих нас точек от средней арифметической на кривых нормального распределения разных переменных. Рассмотрим, какое применение может иметь стандартная оценка.

Допустим, мы имеем статистику общих расходов на образование в среднем на одного ученика в школах в 50 более или менее однотипных городах России. Пусть эти данные имеют вид распределения а (см. рис. 14.4).

Допустим также, что мы имеем данные о средней заработной плате учителей в этих городах в виде распределения в.

Допустим, что мы к тому же имеем данные о выпускниках школ с золотыми медалями в тех же 50 городах. Пусть эта статистика имеет вид распределения с.

Отметим на кривых в виде пунктирных вертикальных линий границы стандартных отклонений, а в виде жирных вертикальных линий – место города А в каждом из распределений.

Мы видим, что стандартная оценка места города А на кривой а равна примерно –1,6, а на кривой в равна –0,8, а вот на кривой с стандартная оценка города А равна +0,8.

Получается, что мы имеем относительно низкие общие расходы на одного ученика в городе А и невысокую среднюю заработную плату учителей в этом же городе, так как оба показателя находятся слева от средних арифметических.

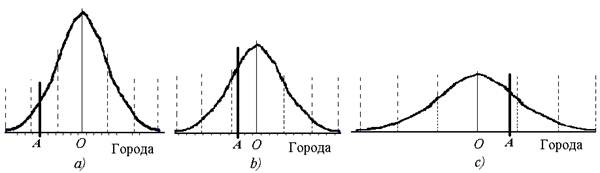
Рис. 14.4. Сравнение стандартных оценок на кривых распределения трех переменных

В то же время мы имеем неожиданно высокий показатель по количеству золотых медалистов в школах этого города, так как этот показатель находится справа от средней арифметической.

Какие выводы можно сделать их такого соотношения стандартных оценок?

Можно, конечно, с готовностью предположить, что меньшие затраты на школьное образование и на заработную плату учителям обеспечивают более высокое качество самого школьного образования. И строить далеко идущие планы.

Но мы сделаем иные выводы. Первый состоит в том, что низкие расходы на образование и низкие зарплаты школьных учителей компенсируются подвижничеством самих учителей города А. Второй вывод состоит в том, что в при сохранении прежними первых двух показателей уже в ближайшем будущем в школах города А скорее всего произойдет понижение и третьего показателя − количество выпускников с золотыми медалями. Потому что подвижничество не может быть нормой и продолжаться бесконечно долго.

Дата добавления: 2014-12-27