Комплексные величины и действия над ними

При анализе электрических и радиотехнических цепей ши­роко используются комплексные величины. Рассмотрим ос­новные сведения о комплексных величинах.

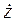
Комплексное число имеет следующие формы представления: алгебраи­ческую, показательную, геометрическую и тригонометричес­кую.

Алгебраическая форма представления комплексного числа:

, (П.1) и т.д.

где - вещественная составляющая, - мнимая составляющая комплексного числа.

Комплексное число в показательной форме имеет вид:

, (П.2)

где 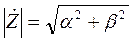- модуль комплексного числа,

- фаза комплексного числа.

Комплексное число может быть представлено в виде век­тора на комплексной плоскости (рис.П.1). Под комплексной плоскостью понимается плоскость, на которой ось абсцисс являет­ся осью вещественных составляющих комплексного числа и обозначается единицей (+1), а ось ординат является осью мнимых составляющих комплексного числа и обозначается 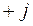. Как видно из рис.П.1, вектор, соответствующий комплексному числу, характеризуется модулем и фазой, как при показатель­ной форме.

Рис.П.1 Представление комплексного числа на комплексной плоскости

Проекция вектора на вещественную ось комплексной плоскости равна вещественной составляющей комплексного числа в алгеб­раической форме, а проекция этого вектора на мнимую ось равна мнимой составляющей комплексного числа в алгебраи­ческой форме (П.1).

Исходя из векторной диаграммы рис.П.1, вытекает тригонометрическая форма представ­ления комплексного числа:

(П.3)

В процессе расчётов возникает необходимость перехода из одной формы представления комплексного числа в другую. Остановимся на этих действиях. Сравнивая (П.2) и (П.3), можно сделать вывод, что из показательной формы представления комплексного числа (П.2) можно перейти к тригонометрической форме (П.3), выполняя очевидные действия.

Сравнивая формулы (П.1) и (П.3), видно, что:

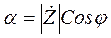, . (П.4)

Соотношения (П.4) показывают, что если необходимо перейти из показательной формы представления комплексного числа (П.2) в алгебраическую форму его представления (П.1) необходимо выполнить действия (П.4).

В процессе расчета возникает необходимость суммирования, вычитания, деления и умноже­ния комплексных чисел. Рассмотрим эти действия над комплексными числами.

Очевидно, что два комплексных числа равны, если равны их, соответственно, вещественные и мнимые части при алгебраической форме представ-

ления (П.1), или равны их модули и фазы при показательной форме представления (П.2).

Рассмотрим два комплексных числа в алгебраической форме:

, .

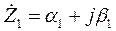Эти же числа в показательной форме (П.2) имеют вид:

, .

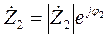Для суммирования или вычитания комплексных чисел их необходимо представить в алгебраической форме. Процесс суммирования (вычитания) состоит в суммировании (вычитании) отдельно вещественных составляющих и отдельно мнимых составляющих комплексных чисел. Тогда сумма (разность) этих чисел будет равна:

. (П.5)

Суммирование и вычитание комплексных чисел можно осуществлять

и в геометрической форме на комплексной плоскости по правилу параллелограмма, т.е. так же, как суммируются вектора. На рис. П.2 показано суммирование векторов на комплексной плоскости.

Нет векторной диаграммы.

Рис.П.2 Векторное суммирование комплексных чисел

Дата добавления: 2014-12-27