Приклад. Графічно вирішити рівняння x lg x=1

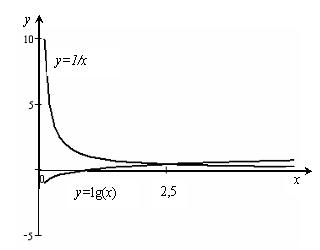Графічно вирішити рівняння x lg x=1

Рішення:

Запишемо рівняння рівністю

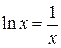
Побудувавши крив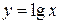і і , наближено знайдемо єдиний корінь .

Метод половинчастого ділення (метод вилки).

Якщо дане рівняння 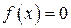, де функція безперервна на 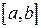і .

Для знаходження кореня рівняння (1), що належить відрізку 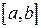, ділимо цей відрізок навпіл. Якщо , то є коренем рівняння. Якщо 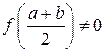, то обираємо ту з половин чи 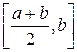, на кінцях яких функція має протилежні знаки. Новий звужений відрізок 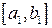знову ділимо навпіл і проводимо те саме розглядання і так далі. В результаті отримаємо на певному етапі чи точений корінь рівняння (1), чи нескінченну послідовність викладених одне в одного відрізків 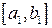, , …, … таких, що

(n = 1, 2, …) (2)

(3)

Так як ліві кінці утворюють монотонну неубутну обмежену послідовність, а перші кінці – монотонну обмежену послідовність, що не зростає, то в силу рівняння (3) існує загальна границя

Переходячи до границі 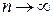в нерівності (2), в силу безперервності функції отримаємо 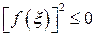. Звідси , тобто ξ є коренем рівняння (1), причому, очевидно, .

Якщо корені рівняння (1) не визначені на відрізку 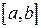, то таким способом можна знайти один з коренів рівняння (1). Метод легко реалізується на ПЕОМ.

Метод ітерацій (послідовних наближень).

Сутність методу. Нехай дане рівняння 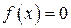, де – безперервна функція, і вимагається знайти його дійсні корені. Замінимо рівняння (1) рівносильним рівнянням

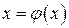(2)

Оберемо будь-яким способом грубо наближені значення кореня 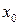і підставимо його в праву частину рівняння (2). Тоді отримаємо певне число

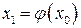(3)

Підставляючи тепер в праву частину рівності (3) замість 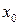число 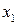, отримаємо нове число 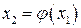. Повторюючи процес, будемо мати послідовність чисел

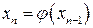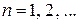, (4)

Якщо ця послідовність – збіжна, тобто існує границя 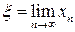, то переходячи до границі в рівності (4) і вважаючи функцію 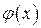неперервною, знайдемо

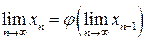
чи

(5)

Таким чином, границя ξ є коренем рівняння (2) і може бути обчислена за формулою (4) з будь-яким ступенем точності.

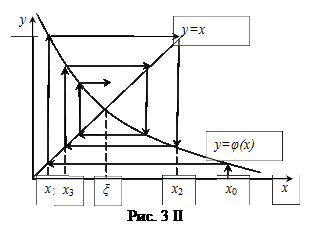
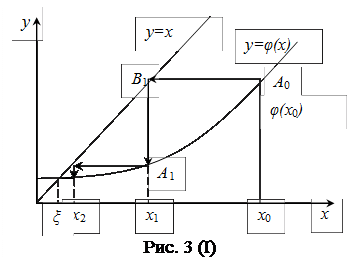Геометричний спосіб інтерполяції може бути пояснений так. Побудуємо на площині Оху графік функції і . Кожен дійсний корінь ξ рівняння (2) є абсцисою точки перетину М кривої з прямою (рис. 3).

Відправляючись від певної точки будуємо ламану…

Метод релаксації.

При інженерних рішеннях рівнянь часто бажано від ітерації до ітерації прискорювати чи уповільнювати зміну функції. Цей спосіб часто використовують для того, щоб уникнути розбіжності при ітераціях.

Позначимо через 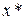значення змінної 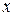на попередній ітерації, тоді маємо

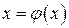(1)

Додамо і віднімемо в правій частині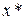

З правого боку знаходиться зміна, отримане на попередній ітерації. Цю зміну можна скорегувати введенням коефіцієнта :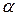

(*)

При збіжності ітерації 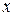стає рівним 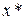. З рівняння (*) витікає, що в наслідок ітерації значення 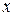задовольняє рівнянню (1).

Якщо – нижня релаксація.

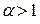– верхня релаксація.

Загального правила для вибору α немає.

Оптимальне α вибирають виходячи з фізично поставленої задачі і попередніх обчислень.

α може мінятися від ітерації до ітерації.

Дата добавления: 2014-12-23