Метод Гауса

Метод послідовного виключення невідомих Гауса є одним з найбільш універсальних та ефективних методів рішення лінійних алгебраїчних систем. Він відноситься до числа прямих методів (тобто дозволяє за кінцеве число дій отримати точне рішення системи; «точне рішення» слід сприймати умовно як характеристику алгоритму, а не реального обчислювального процесу). Рішеня за методом Гауса складається з двох етапів. На першому етапі (прямий хід) система

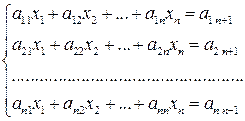(1) чи (1')

приводиться од трикутного вигляду.

На другому етапі (зворотній хід) іде послідовне визначення невідомих з трикутної системи.

Нехай 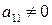. називають ведучим елементом першого кроку. Якщо поміняємо місцями рівняння з номерами 1 та і, де 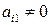. Система вважається невиродженою, такий номер і завідомо знайдеться,починаючи з другого. Для цього помножимо перше рівняння на і складемо його з другим, отримаємо

де

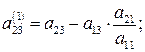
тобто

Після того помножимо перше рівняння на 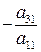і складемо з третім. Отримаємо

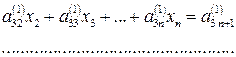
Аналогічно для окремих рівнянь системи від четвертого до n -го:

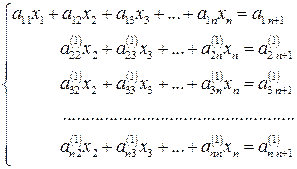(2)

де

Основним результатом цього кроку є система n – 1 порядку з невідомими 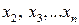, утворена останніми (n – 1) рівняннями системи (2).

Тепер вважатимемо, що елемент ; який називають ведучим елементом другого кроку, відмінний від нуля. У протилежному випадку потрібно провести відповідну перестановку рівнянь. Виключимо змінну 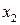з усіх рівнянь системи (2) починаючи з третього. Для цього помножимо друге рівняння на 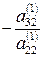та складемо з третім, отримаємо

Потім помножимо друге рівняння на і складемо з четвертим, отримаємо

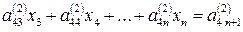
І так далі до n -ого рівняння

Таким чином, перетворена система (2) матиме вигляд

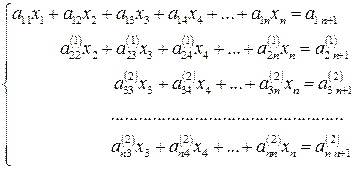(3)

де .

Після n – 1-го кроку прийдемо до системи

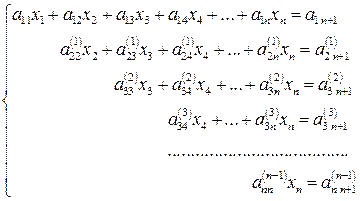(4)

Приведення вихідної системи до трикутного вигляду (4) завершує перший етап побудування рішення методом Гауса.

Другий етап – зворотній хід – полягає у рішенні трикутної системи (4). З останнього рівняння визначається . За знайденим значенням з n – 1-го рівняння визначаємо 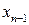. Потім за і 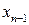з n – 2-го рівняння визначають і так далі до 1-го рівняння, з якого визначають 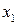. На цьому процес побудови рішень системи (1) закінчується.

Для нашого дискретного аналогу рівняння теплопровідності метод рішення носить назву метод прогонки, в іноземній літературі метод Томаса, чи TDMA (три діагональний матриці алгоритм). Назва обумовлена групуванням невідомих коефіцієнтів матриці вздовж трьох діагоналей.

Наш дискретний аналог має вигляд

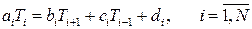
для вузлових точок на границі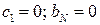

чи

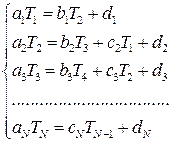
Дата добавления: 2014-12-23