
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение ускорения свободного падения
|
|
|
|
ЛАБОРАТОРНАЯ РАБОТА № 1
Ошибки при косвенных измерениях
Предположим некую измеряемую величину A, которая является функцией нескольких измеряемых во время опыта величин a, b. Как влияют ошибки измерения величин a, b на точность определения величины А? Пусть абсолютные значения погрешностей измеряемых величин a, b равны соответственно ∆a, ∆b, тогда для различных функций зависимости A от измеряемых величин a, b ошибка рассчитывается различным способом (таблица 1.).
Таблица 1
| Действие | абсолютная ошибка ∆А | относительная ошибка ∆А/А |
| A=a+b, A=a−b | 
| 
|
| A=a·b | 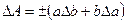
| 
|
| A=an | 
| 
|
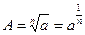
| 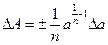
| 
|

| 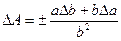
| 
|
Оборудование: Электронный секундомер, выпрямитель ВС-4-12, математический маятник, измерительная лента, стальной шарик.
Задание 1. Определение ускорения свободного падения тела алгебраическим методом
Цель: Изучение свободного падения тел. Определение ускорения свободного падения.
1.Теоретическое введение
Ускорение свободного падения - это физическая величина, которая характеризует быстроту изменения скорости тела массой m, под действием силы тяжести G:  Сила тяжести является равнодействующей двух сил: силы тяготения и центробежной силы инерции. Система координат, жестко скрепленная с Землей, не будет инерциальной системой отсчета, т.к. она не будет двигаться прямолинейно и равномерно (Земля вращается вокруг собственной оси). В неинерциальной системе отсчета, имеющей вращательное движение, на тела будет действовать центробежная сила инерции, направленная по радиусу от центра вращения.
Сила тяжести является равнодействующей двух сил: силы тяготения и центробежной силы инерции. Система координат, жестко скрепленная с Землей, не будет инерциальной системой отсчета, т.к. она не будет двигаться прямолинейно и равномерно (Земля вращается вокруг собственной оси). В неинерциальной системе отсчета, имеющей вращательное движение, на тела будет действовать центробежная сила инерции, направленная по радиусу от центра вращения.
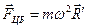 (1)
(1)
Кроме этого, согласно закону всемирного тяготения на тело будет действовать сила тяготения Земли:
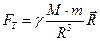 , (2)
, (2)
где М и m - массы Земли и тела соответственно, R - радиус Земли.
|
|
|
Сила тяжести G будет является равнодействующей этих сил и определяться как их векторная сумма:  . Используя формулы (1, 2), получим:
. Используя формулы (1, 2), получим: 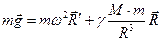 , отсюда:
, отсюда: 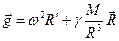 .
.
Полученная формула позволяет сделать вывод о том, что ускорение свободного падения не зависит от массы тела и в земных условиях (w = const, M = const, g = const) будет зависеть только от радиуса окружности вращения тела и расстояния между телом и центром Земли, т.е. от положения тела. В иных условиях (на Луне, Марсе, Венере) ускорение свободного падения примет и иное численное значение, т.к. изменится скорость вращения и масса небесного тела М.
В условиях данного опыта силой сопротивления воздуха можно пренебречь. В этом случае тело будет двигаться равноускоренно только под действием силы тяжести, т.е. оно находится в состоянии свободного падения. Используя кинематическую формулу 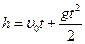 для данного случая (u0 = 0) получим
для данного случая (u0 = 0) получим 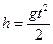 или
или 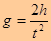 . Таким образом, для определения численного значения ускорения свободного падения необходимо измерить высоту падения тела h и время его падения t. Ознакомьтесь с описанием экспериментальной установки.
. Таким образом, для определения численного значения ускорения свободного падения необходимо измерить высоту падения тела h и время его падения t. Ознакомьтесь с описанием экспериментальной установки.
2.Описание лабораторной установки и метода измерения
Установка (рис. 1) представляет собой стойку, на которой располагается мерная шкала 1. На верхней части стойки закреплен электромагнит 2, удерживающий стальной шарик 3. На стойке установлен датчик 4, который может перемещаться вдоль стойки при помощи крепления 5. При отключении электромагнита включается секундомер, и шарик начинает свободно падать. В момент, когда шарик попадает на датчик, секундомер останавливается.
 3.Порядок выполнения работы
3.Порядок выполнения работы
1. Установите на установке (рис. 1) датчик 4 на определенную высоту h, записав это значение в таблицу 1.
2. При помощи выключателя на электромагните 2, приводят стальной шарик 3 в свободное падение.
3. При попадании шарика на датчик, зафиксируйте время падения шарика на секундомере, записав значение в таблицу 1.
|
|
|
4. Обнулите значение секундомера и переведите датчик в первоначальное состояние (взвести вверх), и повторите опыт не менее 5 раз
5. Проведите тот же опыт для четырех различных положений датчика 4.
4. Обработка результатов измерения
1.По результатам измерения t времени падения шарика, рассчитывают ускорение свободного падения по формуле
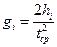 , где
, где
hi - высота, на которую установлен датчик в четырех сериях эксперимента
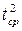 - берется среднее из пяти для каждой данной высоты hi.
- берется среднее из пяти для каждой данной высоты hi.
2. Из получившихся значений gi вычисляют среднее значение ускорения свободного падения по формуле: 
3. Рассчитывают погрешности по формулам:
абсолютную – 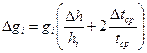
где, Δh инструментальная погрешность, равная половине цены деления измерительной линейки;
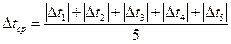 ,
, 
4. Рассчитывают среднее значение абсолютных погрешностей величины ускорения свободного падения: 
5. Определяют относительная погрешность: 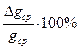 . Результат измерений записывается в виде g= gср± Δgср.
. Результат измерений записывается в виде g= gср± Δgср.
Таблица 1.
| hi, м | № | ti, c | tср, c | Δti= tср-ti, c | Δtср, c | 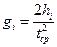 , м⁄с2 , м⁄с2
| Δgi,м⁄с2 |
| h1= | g1= | Δg1= | |||||
| h2= | g2= | Δg2= | |||||
| h3= | g3= | Δg3= | |||||
| h4= | g4= | Δg4= | |||||
| Δh= | 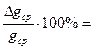
| gср= | Δgср= | ||||
| g= |
Задание 2. Определение ускорения свободного падения методом математического маятника
Цель: Используя математический маятник, определить ускорение свободного падения.
1.Теоретическое введение
В этом методе используется зависимость периода колебаний математического маятника Т от его длины ℓ и ускорения свободного падения: 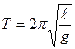 . Уже эта зависимость позволяет определить ускорение свободного падения. Однако, математический маятник - это научная абстракция. Модель математического маятника должна состоять из тонкой, невесомой и нерастяжимой нити, на одном конце которой закреплена материальная точка (рис.2).
. Уже эта зависимость позволяет определить ускорение свободного падения. Однако, математический маятник - это научная абстракция. Модель математического маятника должна состоять из тонкой, невесомой и нерастяжимой нити, на одном конце которой закреплена материальная точка (рис.2).
 Чтобы реальный маятник соответствовал идеальному математическому маятнику, необходимо брать нить максимально возможной длины. Увеличение длины нити приводит к трудностям в ее измерении. Их можно избежать, используя исходную зависимость для маятника с нитью меняющейся длины. В этом случае:
Чтобы реальный маятник соответствовал идеальному математическому маятнику, необходимо брать нить максимально возможной длины. Увеличение длины нити приводит к трудностям в ее измерении. Их можно избежать, используя исходную зависимость для маятника с нитью меняющейся длины. В этом случае:
|
|
|

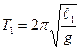 ;
; 
Возведем в квадрат оба уравнения и вычтем из первого второе:
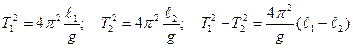
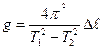 (3)
(3)
 2.Описание лабораторной установки и метода измерения
2.Описание лабораторной установки и метода измерения
Установка (рис. 3), представляет собой массивный металлический шар 1 подвешенный на длинной нити 2. Второй конец нити, перекинутой через кольцо 3 в верхней части стойки, крепится на мерной шкале 4. При изменении положения свободного конца нити вдоль мерной шкалы изменяется, длинна ℓ математического маятника. Разница между показаниями шкалы в двух последовательных опытах, при изменении положения свободного конца нити, и есть величина Δℓ
3.Порядок выполнения работы
1. Установите свободный конец нити на определенное положение на мерной шкале.
2. Отведите маятник на небольшой угол (порядка 10 – 15º) от положения равновесия, отпустив шарик, предоставьте ему свободно колебаться. В какой-либо момент наибольшего отклонения маятника запустите ход секундомера и отсчитайте время t1 в течение, которого маятник совершит n=50 полных колебаний.
3. Измерение времени 50 колебаний производите 3 раза при неизменном положении свободного конца нити (т.е. для неизменной ℓ1).
4. Измените, положение свободного конца нити (т.е. устанавливают новую длину маятника ℓ2) и повторите опыт по определению времени t2 50 колебаний.
5. Результаты занесите в таблицу 2.
4. Обработка результатов измерения
1. Измеряя среднее время tср 50 колебаний, рассчитывают период колебаний для каждой из длин маятника: 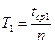

2. Рассчитывают gср, пользуясь формулой (3), где Δℓ= ℓ1 - ℓ2
3. Рассчитывают погрешность: 
погрешности отдельных величин определяют так:
если считать π = 3.14, то Δπ = 0,0016;
Δ l1= Δ l2 и равно половине цены деления шкалы измерительной линейки, т.е. 0,0005 м;
ΔT1, ΔT2 вычисляют по формулам: 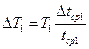 ,
, 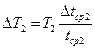 . Для определения tср и Δtср используют формулы:
. Для определения tср и Δtср используют формулы: 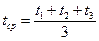 ,
, 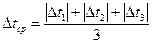 .
.
|
|
|
4. Результат измерения записывают в виде: g= gср± Δgср.
5. Все результаты заносят в таблицу 2. Сделайте вывод по работе.
Таблица 2.
| № | n | ti, c | tср, c | Δti= tср-ti, c | Δtср, c | 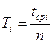 , c , c
| T2, c2 | ΔT | |
| для длинны ℓ1= | |||||||||
| для длинны ℓ2= | |||||||||
| Примечание: ℓ1 > ℓ2 g= |
Выводы:__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
ВОПРОСЫ.
1. Что называется ускорением? Силой?
2. Закон всемирного тяготения. II закон Ньютона. Понятие ускорения свободного падения. Доказательства ускорения свободного падения для данного места Земли.
3. Сила тяготения и сила тяжести. Зависимость силы тяжести и ускорения свободного падения от широты местности и высоты. Показать их на рисунке.
4. Какое движение называется свободным падением? Закон свободного падения
5. Математический маятник. Период колебаний математического маятника.
6. Методы определения ускорения свободного падения. Вывод расчетных формул для g.
7. Приборы и установки.
Для расчетов
дата выполнения_____________________________
Преподаватель_____________________________
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 6243; Нарушение авторских прав?; Мы поможем в написании вашей работы!