Доверительные интервалы для математического ожидания при неизвестной дисперсии

Оценка генеральной дисперсии по исправленной выборочной

Пусть из генеральной совокупности объёмом n извлечена выборка. Требуется по данным выборке оценить неизвестную генеральную дисперсию D_г.

Выборочная дисперсия является смещённой оценкой генеральной дисперсии. Отличие математического ожидания выборочной дисперсии от оцениваемой генеральной дисперсии определяется следующим соотношением:

.

(6.16)

Выборочная дисперсия может быть исправлена. Исправленная выборочная дисперсия равна:

.

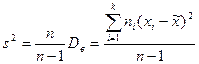(6.17)

Исправленная выборочная дисперсия (6.17) является несмещённой оценкой генеральной дисперсии. Таким образом, получена оценка генеральной дисперсии по исправленной выборочной дисперсии.

Пусть случайая величина Х генеральной совокупности распределена нормально, учитывая, что дисперсия неизвестна. Требуется оценить неизвестное математическое ожидание с помощью доверительных интервалов.

Во-первых, по данным выборки объёмом n можно найти исправленную выборочную дисперсию s ², используя (6.17).

Во-вторых, по данным выборки можно строить случайную величину, которая имеет распределение Стьюдента с k = n–1 степенями свободы, используя формулу (6.8):

.

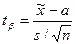(6.18)

Если сравнить распределение Стьюдента по данным выборки (6.18) с (6.8), то следует отметить, что в (6.18):

1. За случайную величину x принята разность (), которая является отклонением неизвестного математического ожидания а от среднего выборочного.
2. За c² принимается исправленная выборочная дисперсия s².

Если в числителе (6.18) заменить разность () на e, то (6.18) можно записать в виде:

.

(6.19)

Из уравнения (6.19) можно найти e – отклонение неизвестного математического ожидания от среднего выборочного:

.

(6.20)

Из уравнения (6.18) можно найти неизвестное математическое ожидание, если известно значение случайной величины t_b, по (6.19), где индекс переменной указывает на особенность задачи с использованием понятия надёжности b в отличие от (6.8). Математическое ожидание записывается в виде доверительного интервала, подставив отклонение e из выражения (6.20) в неравенство (6.11):

.

(6.21)

Если задаться значением надёжности b, то можно найти вероятность попадания в интервал для неизвестного математического ожидания, который строится по аналогии с (6.15):

.

(6.22)

Из уравнений (6.8) и (6.19) видно, что распределение Стьюдента определяется параметром n – объёмом выборки (числом степеней свободы k=n–1) и не зависит от неизвестных параметров а и s. Эта особенность является его большим достоинством.

Можно сформулировать алгоритм отыскания границ доверительного интервала для математического ожидания, если неизвестна дисперсия D = s²:

1. Задают значение надёжности в формуле (6.22) – b.
2. Находят значение t_b, пользуясь таблицей Приложения 2 по значениям k и уровню значимости a = 1– b, выбрав верхний вариант: [Уровень значимости a (двусторонняя крит. область)].
3. Из уравнения (6.20) находят отклонение неизвестного математического ожидания от среднего выборочного – e.
4. Строится доверительный интервал по (6.21) или (6.11), содержащий неизвестное математическое ожидание с вероятностью b.

Пример 6.

Случайная величина Х имеет нормальное распределение. По выборке объёма n=61 найдена выборочная средняя`x =30 и исправленное среднее квадратическое отклонение s = 1,5. Найти доверительный интервал для оценки с надёжностью b=0,95 неизвестного математического ожидания – а.

Решение. Дано по условию задачи:

1. Исправленное среднее квадратическое отклонение s = 1,5.
2. Выборочная средняя`x =30.
3. Надёжность b = 0,95;
4. Объём выборки n = 61.

Пользуясь таблицей приложения 2 по значениям k = n – 1 = 60 и уровню значимости a = 1 – b = 1–0,95 = 0,05 находим значение t_b=2,00.

Вычисляем по формуле (6.20):

Полученное значение e подставим в формулу доверительного интервала (6.11): 30 – 0,387 < a < 30+ 0,387.

Доверительный интервал для неизвестного математического ожидания с надёжностью b = 0,95 равен: 29,613 < a < 30,387.

Глава 7. Проверка статистических гипотез

Дата добавления: 2014-12-27