
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Первая интерполяционная формула Ньютона
|
|
|
|
Пусть функция y = f(x) задана в n+1 равноотстоящих узлах 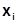 , i = 0, 1, 2, …, n, с шагомh. Требуется найти интерполяционный многочлен Pn(x) степени не выше n, удовлетворяющий условию:
, i = 0, 1, 2, …, n, с шагомh. Требуется найти интерполяционный многочлен Pn(x) степени не выше n, удовлетворяющий условию:
Pn(xi) = yi, i =0, 1, 2, …, n. (6.3.3-2)
Будем искать интерполяционный многочлен вида:
Pn(x) =a0 + a1(x-x0) + a2(x-x0)(x-x1) + …+ an(x-x0)(x-x1)…(x-xn-1),(6.3.3-3)
где аi, i =0,1,2,…,n–неизвестные коэффициенты, не зависящие от узлов интерполяции.
Для нахождения коэффициентов формулы Ньютона аi будем подставлять в
(6.3.3-3) значения х, совпадающие с узлами интерполяции, требуя выполнения условия (6.3.3-2).
Пусть х = x0, тогда, согласно (6.3.3-2), Pn(x0) = y0 = a0. Следовательно, a0 = y0.
Пусть х = x1, тогда
Pn(x1) = y1 = a0 + a1(x1-x0) = y0 + a1(x1-x0). (6.3.3-4)
Из равенства (6.3.3-4) следует, что 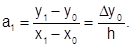
Теперь пусть х = х2, тогда:
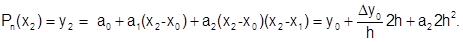
Выражая неизвестный коэффициент, получим:

Продолжая подстановку, можно получить выражение для любого коэффициента с номером i:
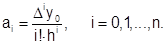
Подставив найденные значения коэффициентов в (6.3.3-4), получим первую интерполяционную формулу Ньютона:
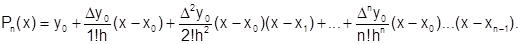 (6.3.3-5)
(6.3.3-5)
Воспользуемся этой формулой, как одной из возможных форм записи интерполяционного многочлена второй степени.
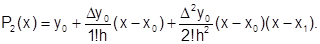 (6.3.3-6)
(6.3.3-6)
Тогда для вычисления значения функции, заданной табл. 6.3.3-1, при х = 1.45:
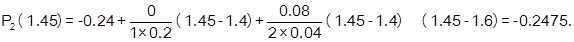
Отметим, что при использовании первой интерполяционной формулы Ньютона целесообразно выбирать х0близко к точке интерполяции (интерполяция вперед). Это обеспечивает более высокую точность при фиксированном числе узлов. Запись интерполяционного многочлена в виде первой формулы Ньютона позволяет учитывать дополнительные узлы в правой части таблицы, уточняя ранее полученный результат, без пересчета остальных слагаемых.
Введя обозначение:  и проведя несложные преобразования вида:
и проведя несложные преобразования вида: 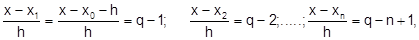 приведем (6.3.3-5) к виду:
приведем (6.3.3-5) к виду:
|
|
|
 (6.3. 3-7)
(6.3. 3-7)
Это второй вид записи формулы Ньютона для интерполирования вперед. Она применяется для интерполяции f(x) в окрестностях начального значения х0, где q – достаточно мало по абсолютной величине.
Если n=1, то из (6.3.3-6) получаем формулу линейной интерполяции 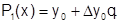
Если n=2, то получаем формулу квадратичной (или параболической) интерполяции
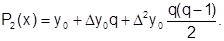
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 503; Нарушение авторских прав?; Мы поможем в написании вашей работы!