Конечноразностные формулы

Часто требуется найти производные от функций, заданных на равномерной сетке и не в произвольной точке, а в узле сетки. Тогда можно получить формулы более простые, чем в общей постановке. Разложим в ряд Тейлора функцию у(х) в окрестности i-го для соседних с i-м узлом:

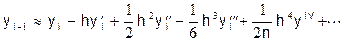
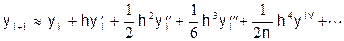(2)

Здесь h-шаг сетки.

Конечноразностные формулы получаем, привлекая из формул (2) необходимые уравнения и удерживая в них необходимое число слагаемых. Полученная система уравнений решается относительно интересующей нас производной.

Например, удерживая в третьем равенстве (2) три слагаемых и решая его относительно y_i^¢, получаем

(3)

Первое слагаемое в правой части является рабочей формулой. Второе слагаемое - главный член погрешности, по которому априорно можно оценить только порядок точности (первый).

Аналогичную формулу можно получить из второго равенства (2):

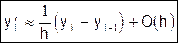(4)

Здесь О(h) - величина первого порядка малости относительно h. Формула (3) называется правой, (4) - левой.

Центральная формула, использующая симметрично расположенные узлы, получается после вычитания второго равенства (2) из третьего и решения относительно y_i^¢:

(5)

Порядок точности ее повышен (второй), поскольку слагаемое с y_i^¢¢, дающее главный член погрешности первого порядка, оказался исключенным.

Сложив второе и третье равенства (2), можно получить формулу для второй производной второго порядка точности:

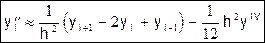(6)

Привлекая все равенства (2) можно получить формулы для третьей и четвертой производных:

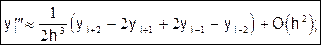(7)

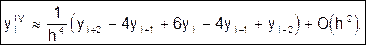(8)

В краевых точках сетки (i=0, n) невозможно использовать центральные конечноразностные формулы. Правую формулу для первой производной второго порядка точности получают, используя два последних равенства (2) и исключая из них члены со второй производной:

(9)

Аналогично, привлекая дополнительно ряд Тейлора для (i+3)-го узла, получают формулу для второй производной:

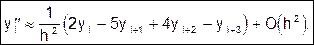(10)

Соответствующие левые формулы имеют вид

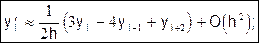(11)

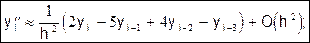(12)

Дата добавления: 2014-12-27