Нестандартные случаи интегрирования

Вычисление интеграла 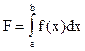от функции, разрывной в точке х=с (а<с<в), возможно с высокой точностью, если интеграл предварительно представить в виде

(27)

Аналогичное разбиение интеграла имеет смысл и тогда, когда разрыв имеют производные подынтегральной функции.

Вычисление несобственного интеграла 1-го рода

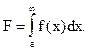(28)

возможно численно, если сначала привести его к интегралу в конечных пределах от 0 до 1 с помощью замены переменной

x=a/(1-t). (29)

Для вычисления несобственного интеграла 2-го рода вида

(30)

можно применить метод аддитивного выделения особенности. Для этого функция j (x), не имеющая особенностей, представ­ляется в виде

(31)

где 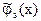— усеченный ряд Тейлора s-й степени для функции в окрестности точки x=а:

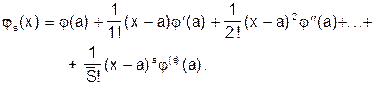(32)

Тогда интеграл (30) примет вид

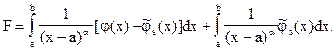(33)

Нетрудно убедиться в том, что подынтегральная функция в первом интеграле непрерывна вместе со всеми производными вплоть до s-го порядка. Для ее интегрирования можно применять известные квадратурные формулы. Второй интеграл в (33) — несобственный 2-го рода, но подынтегральная функция в нем — степенная и легко интегрируется аналитически.

4.8. Вычисление кратных интегралов

Требуется вычислить двойной интеграл по прямоугольной области

(34)

Для получения кубатурной формулы приближенного интегрирования представим (34) в виде

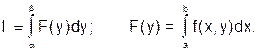(35)

Для вычисления этих однократных интегралов применим известные квадратурные формулы

(36)

Окончательно

(37)

Такой метод получения кубатурных формул называется методом последовательного интегрирования. Он легко обобщается на случай интегралов более высокой кратности.

Этот метод можно применить и для вычисления интегралов на области произвольной формы:

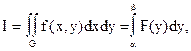(38)

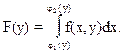(39)

Применяя квадратурную формулу для интеграла (38), получим

(40)

Значения F(y_i) вычисляются согласно (39) с использованием квадратурных формул, тип которых обычно зависит от у, так как пределы интегрирования переменных.

Результаты данного подраздела легко обобщаются на интегралы более высокой кратности.

4.9.Метод ячеек

Наиболее простая и весьма эффективная кубатурная формула для прямоугольной области получается в результате применения по обеим независимым координатам формул средних. Тогда равенства (36) примут вид

(41)

(42)

где `x=(a+b)/2, `y=(a+b)/2. Подставив (42) в (43), получим кубатурную формулу

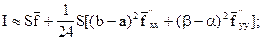(43)

Здесь s=(b-a)(b-a) - площадь области интегрирования; `f, `f_xx^’’ , `f_yy^’’ - значения подынтегральной функции и ее производных в центре этой области.

Полученная формула имеет второй порядок точности, но так как интервалы интегрирования обычно не малы, то применяют обобщение этой формулы. Интегралы интегрирования делят на подынтервалы узлами 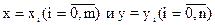и применяют формулы (43) на каждой прямоугольной подобласти:

(44)

Здесь — площади подобластей; 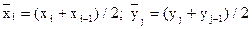— координаты их центров тяжести. Если сетка равномерна, то Sij=S, xi-xi-1=h, yi-yi-1=l и

(45)

Если область интегрирования - не прямоугольник, то ее делят прямоугольной сеткой на р подобластей G_k(k=`1,`p) и тогда

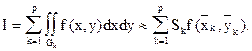(46)

Здесь не записана главная часть погрешности и оценивать погрешность формулы следует апостериорно.

Внутренние подобласти G_k имеют форму прямоугольников. Подобласти, примыкающие к границе области интегрирования, являются криволинейными треугольниками либо трапециями. Второй порядок точности формулы (45) сохранится, если криволинейные участки границы спрямить, что упростит вычисления. В этой формуле S_k — площадь к-й подобласти; `x<sub>k</sub>, `y_k - координаты ее центра тяжести.

Дата добавления: 2014-12-27