
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Общий подход к построению проекционных методов
|
|
|
|
Проекционные методы и подпространства Крылова
Ускорение сходимости релаксационных методов
Скорость сходимости методов, основанных на расщеплении, непосредственно связана со спектральным радиусом матрицы K –1 R; с другой стороны, выбор K ограничен требованием легкой обратимости. Одним из распространенных способов улучшения сходимости является введение параметра. Пусть w– некоторое вещественное число. Рассмотрим вместо системы (1.1) масштабированную систему
| wAx=wb, | (2.10) |
и вместо (2.1) воспользуемся представлением
| wA=(D–wE)–(wF+(1–w)D), | (2.11) |
где матрицы D, E, F имеют тот же смысл, что и в (2.1).
Тогда на основании (2.10) и (2.11) можно построить итерационную схему, похожую на метод Гаусса-Зейделя,
| (D–wE)x k +1=(wF+(1–w)D)x k +wb. | (2.12) |
Схема (2.18) называется методом последовательной верхней релаксации (SOR). Для нее
| KSOR(w)=D–wE RSOR(w)=wF+(1–w)D. |
Выбор параметра w, минимизирующего спектральный радиус является, вообще говоря, достаточно сложной проблемой. Однако для многих классов матриц такая задача исследована и оптимальные значения w известны.
Выражение (2.11) остается тождеством, если в нем поменять местами матрицы E и F. Такая перестановка дает обратный метод последовательной верхней релаксации:
| (D–wF)x k +1=[wE+(1–w)D]x k +wb. |
Последовательное применение прямого и обратного методов SOR дает симметричный метод последовательной верхней релаксации (SSOR)
| (D–wE)x k +1/2=[wF+(1–w)D]x k +wb; (D–wF)x k +1=[wE+(1–w)D]x k +1/2+wb. |
Рассмотрим систему (1.1) и сформируем для нее следующую задачу. Пусть заданы некоторые два подпространства K Ì RN и L Ì RN. Требуется найти такой вектор x Î K, который обеспечивал бы решение исходной системы, «оптимальное относительно подпространства L», т.е. чтобы выполнялось условие
|
|
|
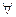 l Î L: (Ax, l)=(b, l), l Î L: (Ax, l)=(b, l),
|
называемое условием Петрова-Галеркина. Сгруппировав обе части равенства по свойствам скалярного произведения и заметив, что b – Ax = r x, это условие можно переписать в виде
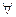 l Î L: (rx, l)=0, l Î L: (rx, l)=0,
| (2.13) |
т.е. r x= b – Ax ^ L. Такая задача называется задачей проектирования x на подпространство K ортогонально к подпространству L.
В более общей постановке задача выглядит следующим образом. Для исходной системы (1.1) известно некоторое приближение x 0 к решению x *. Требуется уточнить его поправку d xÎ K таким образом, чтобы b – A (x 0+ d x) ^ L. Условие Петрова-Галеркина в этом случае можно записать в виде
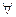 l Î L: (rx0+dx, l)=((b–Ax0)–Adx, l)=(r0–Adx, l)=0. l Î L: (rx0+dx, l)=((b–Ax0)–Adx, l)=(r0–Adx, l)=0.
|
Пусть dim K =dim L = m (где dim – размер подпространств). Введем в подпространство K и L базисы 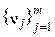 и
и  соответственно. Нетрудно видеть, что (2.19) выполняется тогда и только тогда, когда
соответственно. Нетрудно видеть, что (2.19) выполняется тогда и только тогда, когда
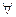 j (1£ j £ m): (r0–Adx,w j)=0. j (1£ j £ m): (r0–Adx,w j)=0.
| (2.14) |
При введении для базисов матричных обозначений V =| n 1| n 2|¼ | n m | и W =| w 1| w 2|¼ | w m | можно записать d x= Vy где yÌ Rm – вектор коэффициентов. Тогда (2.14) может быть записано в виде
| W T (r0–AVy)=0, | (2.15) |
откуда W T AVy = W T r 0 и
| y=(W T AV)–1W T r0. | (2.16) |
Таким образом, решение должно уточняться в соответствии с формулой
| x1=x0+V(W T AV)–1W T r0, | (2.17) |
из которой сразу вытекает важное требование: в практических реализациях проекционных методов подпространства и их базисы должны выбираться, так чтобы W T AV либо была малой размерности, либо имела простую структуру, удобную для обращения.
Из (2.15) также вытекает соотношение
| Vy=A–1r0=A–1(b–Ax0)=x*–x0, |
т.е. Vy = d x представляет собой проекцию на подпространство K разности между точным решением и начальным приближением.
Пусть имеется набор пар подпространств  таких, что K 1Å K 2Å… Kq Å= RN и L 1Å L 2Å… Lq Å= RN (запись K Å L обозначает симметричную разность множеств K и L, т.е. элемент принадлежит K Å L, если он находится либо в K, либо в L, но не в пересечении K и L, т.е. K Å L = K È L – K Ç L). Тогда очевидно, что последовательное применение описанного ранее процесса ко всем таким парам приведет к решению x q, удовлетворяющему исходной системе Ax = b. Соответственно, в общем, виде алгоритм любого метода проекционного класса может быть записан следующим образом:
таких, что K 1Å K 2Å… Kq Å= RN и L 1Å L 2Å… Lq Å= RN (запись K Å L обозначает симметричную разность множеств K и L, т.е. элемент принадлежит K Å L, если он находится либо в K, либо в L, но не в пересечении K и L, т.е. K Å L = K È L – K Ç L). Тогда очевидно, что последовательное применение описанного ранее процесса ко всем таким парам приведет к решению x q, удовлетворяющему исходной системе Ax = b. Соответственно, в общем, виде алгоритм любого метода проекционного класса может быть записан следующим образом:
|
|
|
| Начало |
| Выбор пары подпространств K и L |
| Построение для K и L базисов V=|n1|n2|¼ |n m | и W=|w1|w2|¼ |w m | |
| r=b–Ax |
| y=(W T AV)–1W T r |
| x=x+Vy |
| Продолжать до достижения сходимости |
2.2.2 Случай одномерных подпространств K и L
Наиболее простой ситуацией является случай, когда пространства K и L одномерны. Пусть K и L подпространства являющиеся множествами векторов представимых в виде линейной комбинации векторов { n 1, n 2,…} и { w 1, w 2,…} т.е. K =span{ n } и L =span{ w }. Тогда (2.17) принимает вид
| x k +1=x k +g k n k, | (2.18) |
причем коэффициент g k легко находится из условия ортогональности r k – A (g k n k) ^ w k:
| (r k –Ag k n k, w k)=(r k, w k)–g k (An k, w k)=0, |
откуда g k =(r k, w k)/(An k, w k).
Если выбрать n k = w k = r k, тогда (2.18) принимает вид
| x k +1=x k +r k (r k, r k)/(Ar k, r k). | (2.19) |
Поскольку выражение в знаменателе представляет собой квадратичную форму r kT Ar k, сходимость процесса гарантирована, если матрица A является симметричной и положительно определенной. Данный метод называется методом наискорейшего спуска. В практических задачах метод наискорейшего спуска обладает достаточно медленной сходимостью.
При выборе n k = A T r k и w k = An k формула (2.18) примет вид
| x k =1=x k +A T r k (r k, AA T r k)/(AA T r k, AA T r k)= =x k +A T r k (A T r k, A T r k)/(A T AA T r k, A T r k). | (2.20) |
Данный метод называется методом наискорейшего уменьшения невязки; условием его сходимости является невырожденность матрицы A. Сравнивая (2.19) и (2.20), нетрудно убедится, что метод наискорейшего уменьшения невязки совпадает с методом наискорейшего спуска, примененным к системе A T Ax = A T b.
Если положить K = L и на различных итерациях в качестве вектора n k циклически с повторением выбирать единичные орты e 1, e 2,…, e N, e 1,…то получится рассмотренный ранее метод Гаусса-Зейделя (обратный порядок выбора соответствует обратному методу Гаусса-Зейделя).
Выбор на k -й итерации n k = w k = A T e k дает, так называемый, ABS-класс методов. Чтобы для различных итераций выполнилось условие Ki ^ Kj, возможно либо хранение всех n k с их ортогонализацией по мере нахождения (схема Хуанга), либо пересчет матрицы A (схема Абрамова). Первый вариант ведет к увеличению расходов памяти для реализации алгоритма, второй – к изменению заполненности матрицы. Следовательно, данные методы пригодны лишь для решения небольших систем; с другой стороны, их единственным условием сходимости является существование решения как такового, а потому данный класс пригоден для СЛАУ с вырожденными и неквадратными матрицами. Непосредственно из определения векторов n k следует, что в данных методах на k -й итерации поправка к решению вычисляется из условия обращения k -го уравнения в тождество. Если предполагать, что матрица A квадратная и невырожденная, вычислительная схема имеет следующий вид (вариант с пересчетом матрицы, метод ABR1ORT):
|
|
|
Алгоритм метода ABR1ORT
| Выполнять для i =1,…, N |
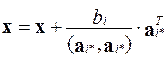
|
| Выполнять для j = i +1,…, N |
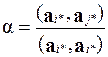
|
| a j* =a j* –a×a i* |
| bj = bj –a× bi |
| увеличить j |
| увеличить i |
Пример использования метода ABR1ORT в системе TALGAT:
- действительный случай: SET "solve" ABR1ORT_r real_m right_r;
- комплексный случай: SET "solve" ABR1ORT complex_m right_c;
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 842; Нарушение авторских прав?; Мы поможем в написании вашей работы!