Преобразование формы математической модели динамического объекта

Математическая модель оптимизируемого объекта может быть представлена в различных формах: графы, структурная схема, система дифференциальных или разностных уравнений… При синтезе чаще используют модель системы в виде структурной схемы. Для решения задачи параметрической оптимизации удобнее работать с моделью в виде системы дифференциальных уравнений первого порядка. Следовательно, необходимо выполнить преобразование структурной схемы к системе дифференциальных уравнений.

Структурная схема системы представляет собой совокупность элементарных звеньев объекта и связей между ними, причем звенья изображаются прямоугольниками с передаточными функциями:

.

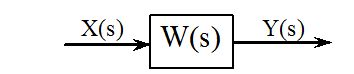Здесь 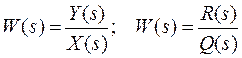- передаточная функция звена, X(s) и Y(s) – изображения входного и выходного сигналов, R(s) и Q(s) – алгебраические полиномы от s, s – оператор Лапласа.

Для перехода от структурной схемы к дифференциальным уравнениям необходимо по передаточной функции каждого звена получить соответствующее ему дифференциальное уравнение. Из курсов «Теория Автоматического Управления» и «Математические Модели» известно, что математические модели звеньев в пространстве Лапласа и временной области тождественны (изоморфны), если они записаны в операторной форме: типа «вход – выход».

Из определения передаточной функции звена следует операторное уравнение «вход – выход»:

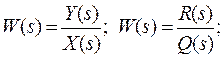
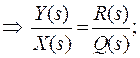
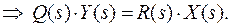
Полученное уравнение с точностью до коэффициентов идентично дифференциальному уравнению того же звена:

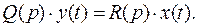
Здесь 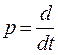- оператор дифференцирования, t – время.

Данное дифференциальное уравнение в дальнейшем приводится к системе дифференциальных уравнений первого порядка (в общем случае), записанных в форме Коши.

В структурных схемах различают следующие элементарные звенья:

1. Пропорциональное звено(Идеальный усилитель):

К – некоторый коэффициент, число.

Операторное уравнение для данного звена имеет вид: Y(s) = K * X(s). Ему соответствует вырожденное алгебраическое уравнение: y(t) = K * x(t).

2. Интегрирующее звено (Интегратор):

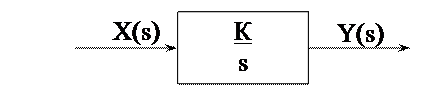
Передаточная функция этого звена: .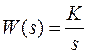

В соответствии с определением передаточной функции имеет место соотношение , из которого следует операторное уравнение «вход – выход»: , а после замены оператора Лапласа s на оператор дифференцирования 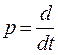можно получить дифференциальное уравнение: 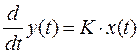, которое обычно записывается в виде: .

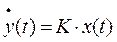3. Реальный усилитель (Апериодическое звено):

Выполняя аналогичные действия, последовательно получают:
, откуда уравнение «вход – выход»: 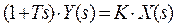, затем, после замены оператора s на p, дифференциальное уравнение: , которое в форме Коши будет иметь вид: .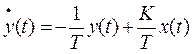

4. Звено второго порядка(Колебательное звено ):

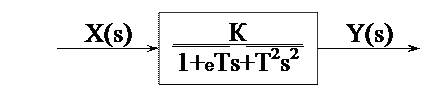
Как и ранее, получают: 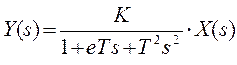, затем операторное уравнение «вход – выход»: , откуда - дифференциальное уравнение второго порядка:

или

.

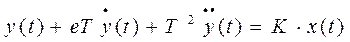Последнее уравнение необходимо привести к системе дифференциальных уравнений первого порядка. Данное преобразование можно выполнить множеством способов. Наиболее употребительным является способ приведения к системе дифференциальных уравнений в нормальной форме с использованием вектора фазовых переменных.

Таким образом, с помощью замены переменных:

,

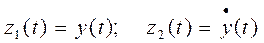вместо исходного уравнения второго порядка получают систему двух дифференциальных уравнений первого порядка в форме Коши:

5. Сумматор:

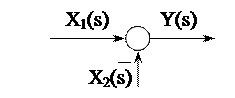
Данному элементу структурной схемы соответствует два алгебраических уравнения: в операторах Лапласа - и во временной области - .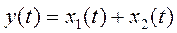

6. Форсирующее звено (Регулятор или Корректирующее устройство):

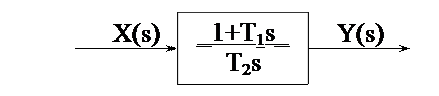
Для преобразования математической модели форсирующего звена передаточная функция записывается в виде:

.

Измененной передаточной функции соответствует структурная схема:

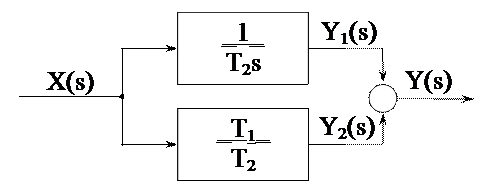
для которой по описанной ранее методике получают дифференциальное уравнение:

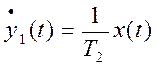
и два алгебраических:

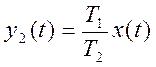и .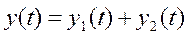

Так как математическая модель объекта призвана отражать в математической форме свойства этого объекта, то имеет смысл учесть и такую особенность некоторых звеньев, как ограничение их выходных сигналов.

Чаще всего ограничению подвержены сигналы в корректирующих устройствах (регуляторах). Для рассматриваемого звена это переменные y(t) и y₁(t), то есть выходной сигнал регулятора и его интегральная составляющая соответственно.

Реализация ограничения значений y₁(t) выполняется с учетом правила:

если переменная достигла своего крайнего значения и собирается его перейти – выйти за границу области допустимых значений (об этом можно судить по знаку производной - 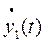), то значение производной требуется «обнулить».

Ограничение сигнала y(t) выполняется с помощью стандартной «срезки»:

если значение переменной вышло за границу области допустимых значений, то выполняется корректировка путем записи в переменную граничного значения.

Описанные процедуры учета ограничений применяются в программных реализациях с использованием соответствующих операторов:

· для интегральной составляющей выходного сигнала регулятора:

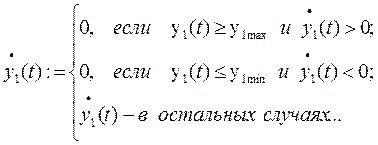
· для выходной переменной регулятора:

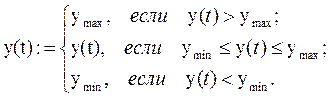
или, с использованием кусочно-линейного оператора:

.

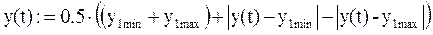После того, как для всех элементов (звеньев) структурной схемы динамического объекта получены соответствующие им дифференциальные и алгебраические уравнения, выполняется сведение полученного набора выражений к системе дифференциальных уравнений в форме Коши. Для этого вводится вектор состояния системы, размерность которого равна количеству имеющихся дифференциальных уравнений, и выполняется соответствующая замена переменных.

На следующем этапе преобразования математической модели строится программная модель, где организовано решение полученной системы дифференциальных уравнений одним из известных методов. Наиболее часто для решения задачи Коши используется программа RKF45 из вычислительного пакета Дж. Форсайта.

Дата добавления: 2014-12-27