
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Округление чисел
|
|
|
|
Округлением числа называют уменьшение количества цифр числа путем отбрасывания одной или нескольких последних цифр (если отбрасываются цифры целой части, то их надо заменять нулями).
При округлении приближенного числа результат тоже получается приближенным. При округлении точных значений чисел в большинстве случаев получаются приближенные значения. Исключение составляет случай, когда отбрасывают один или несколько нулей в конце десятичной дроби. Например: 45,700=45,7.
Существует три способа округления:
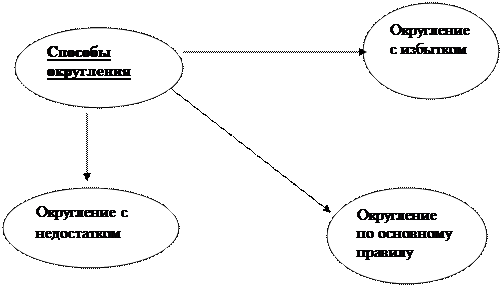
1). При округлении с избытком цифру последнего справа разряда, сохраняемого в числе, всегда увеличивают на единицу.
Например: 67,48 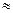 67,5
67,5
3,521 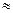 3,53 и т.д.
3,53 и т.д.
В следующих примерах округление числовых значений может быть по смыслу выполнено только с избытком.
1) При подготовке «опыта Торричелли» было подсчитано, что для заполнения трубки необходимо иметь 24 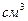 ртути. Это число можно округлить до 30
ртути. Это число можно округлить до 30 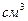 , но не до 20
, но не до 20 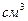 , так как в последнем случае трубка не будет заполнена ртутью полностью и опыт не получится.
, так как в последнем случае трубка не будет заполнена ртутью полностью и опыт не получится.
2) При подсчете первой космической скорости полученный результат можно округлять только с избытком, так как превышение скорости изменит лишь форму орбиты спутника (вместо окружности – эллипс), а занижение скорости приведет к тому, что спутник не выйдет на орбиту и вернется на Землю.
2) При округлении с недостатком цифра последнего разряда, сохраняемого в числе, всегда остается без изменения.
Например: 67,48 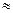 67,4
67,4
3,521 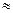 3,52
3,52
Примеры округления с недостатком:
1) При расчете поршня цилиндра значение диаметра следует округлять с недостатком, так как при округлении с избытком поршень может не войти в цилиндр.
2) Напряжение в электрической сети 127 В часто округляют до 120 В. Такое округление производят потому, что понижение напряжения – явление более вероятное (вследствие перегрузки сети и падения напряжения на подводящих проводах).
3) Округление по основному правилу: если первая отброшенная цифра равна 5 или больше 5, то последнюю из сохраняемых цифр увеличивают на единицу; если первая отброшенная цифра меньше 5, то последнюю из сохраняемых цифр оставляют без изменения.
Примеры:
1) Округление чисел, взятых из математических и физических таблиц, в которых эти числа даны с высокой точностью:
а) 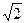 = 1,4142135
= 1,4142135 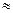 1,41
1,41
б) 
в) известное значение температуры 4 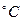 , при котором вода обладает максимальной плотностью, является округленным значением числа 3,98
, при котором вода обладает максимальной плотностью, является округленным значением числа 3,98 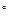 С.
С.
2) Округление переводных множителей для некоторых величин (некоторые из них точные, а некоторые – приближенные с высокой точностью):
1 л.с = 735,499 Вт 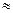 735 Вт
735 Вт
3) В теме «Строение атома» рассматривают массовое число, которое является округленным значением относительной атомной массы элемента:
| Элементы | Атомная масса | Массовое число |
| Цинк | 65,38 | |
| Стронций | 87,63 | |
| Золото | 197,0 |
Как видим, при определении массового числа выполняют округление по основному правилу (в последнем случае – с нулевой погрешностью).
|
Пример: 264213 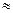 264000=2,64
264000=2,64 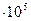 .
.
2) Иногда округление производят с избытком до разряда, в котором стоит цифра 9.
Например: 2,96 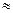 3,0
3,0
В числе может быть несколько девяток, например скорость света в вакууме равна
299793 км/с. При округлении до сотен тысяч получаем 300000км/с.
sin 87 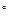 - 0,9986
- 0,9986 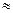 1,00 (при округлении до сотых).
1,00 (при округлении до сотых).
Выполните задания:
1. Как нужно округлить следующие числа?
Ответ оформите в виде таблицы:
| О К Р У Г Л Е Н И Е | ||
| с избытком | с недостатком | по основному правилу |
a. Показание электросчетчика 0342,9 кВт 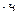 ;
;
b. Подсчитали, что электропроводку нужно выполнить медным проводом сечением 1,76 мм2;
c. Расчет показал, что в качестве защитного сопротивления нужно использовать лампу мощностью 65Вт;
d. В сеть нужно включить предохранитель на силу тока 8А;
e. Ускорение свободного падения равно 9,8 м/с2 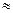 10 м/с2;
10 м/с2;
f. Морская миля равна 1,852 км 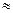 1,8 км;
1,8 км;
g. Экваториальный радиус Земли равен 6380 км 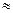 6400 км = 6,4
6400 км = 6,4 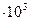 км;
км;
h. Скорость звука в воздухе (0 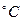 ) равна 331,63 м/с
) равна 331,63 м/с 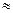 332 м/с;
332 м/с;
i. Электрическая постоянная равна
Ео= 8,854304 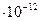 ф/м
ф/м 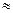 8,85
8,85 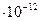 ф/м.
ф/м. 
2. Округлить по основному правилу следующие числа:
1) до единиц: плотность урана 19,1 г/см3;
удельную теплоту плавления свинца 25,0 кДж/кг;
2) до десятков: температуру воды 374 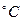 ;
;
температуру плавления свинца 327 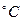 ;
;
3) до сотен: теплоту сгорания дров 8300 кДж/кг;
4) до тысяч: скорость света в вакууме 299793 км/с;
5) до десятых: коэффициент трения дерева по земле 0,71;
удельное сопротивление ртути 0,958 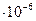 Ом
Ом 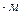 ;
;
6) до сотых: плотность ртути 13,5955 г/см3;
постоянная Авогадро 6,02322 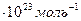 .
.
- Абсолютная и относительная погрешности
При работе с приближенными величинами следует:
i. оценить необходимую точность приближения при измерении;
ii. выполнить действия в границах необходимой точности;
iii. оценить степень точности результата.
Рассмотрим следующие примеры:
Пример 1 Пусть масса некоторого тела больше 19 г., но меньше 20 г., т.е. 19<m<20.
Значит: 19 – приближенное значение массы с недостатком.
20 – приближенное значение массы с избытком.
Границы: 19 – нижняя;
20 – верхняя.
Замечание: в качестве других границ можно выбрать числа меньше 19, но больше 20.
Зная границы значений некоторой величины, можно оценить значения другой величины, зависящей от первой.
Пример 2 Пусть 2,5<x<3,2. Найти границы:
а) 2x
б) 5x-3
в) 
Решение: а) 2,5 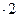 <2x<3,2
<2x<3,2 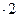 5 –нижняя граница
5 –нижняя граница
5<2x<6.4 6,4 – верхняя граница
Н.Г. В.Г.
б) 12,5< 5x <16 9,5 – нижняя граница
12,5-3 < 5x-3 <16-3 13 – верхняя граница
9,5 <5x -3 <13
Н.г. В.г.
в) x> 0, т.к. x >2,5, то  <
< 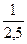 или
или  <
< 
x <3,2, то  <
< 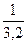 или
или  >
> 
Таким образом:  <
<  <
<  или 0,3125 <
или 0,3125 <  < 0,4
< 0,4
Н.г. В.г.
Пример 3 Пусть 0,5 < a < 1,4; 2< c < 4,1.
Найти границы (а + с) и (а – с).
Решение: 0,5 + 2 < а + с < 1,4 + 4,1 или 2,5 < а + с <5,5
Н.г. В.г.
а – с = а + (-с)
!!! -2 > -с > -4,1, т.е. -4,1 < –с < -2.
0,5 – 4,1< а-с < 1,4 - 2 или -3,6< а-с <- 0,6
Н.г. В.г.
Пример 4 Пусть 1,3 < x < 2,4 и 0,5 < y < 1,1
Найти границы 
Решение: 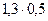 < xy <
< xy < 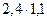 или 0,65 < xy < 2,64
или 0,65 < xy < 2,64
Н.г. В.г.
Приближенные значения величин, полученные в процессе счета, измерения или вычисления могут быть найдены с различной точностью, поэтому важно знать отклонение приближенного значения величины от ее точного значения.
Количественной характеристикой точности приближенного значения величины является погрешность приближения.
Погрешность приближения – это разность между точным (x) и приближенным (а) значениями искомой величины.
Пример 5 если число x= 4,28 заменим приближенным значением а = 4,2 (с недостатком), то допустим погрешность x- а = 0,08, а если заменим приближенным значением b = 4,3 (с избытком), то допустим погрешность x-b = -0,02.
Замечание: погрешность приближения с недостатком – положительная, а с избытком – отрицательная.
Чтобы установить, какое из приближений является лучшим, следует сравнить погрешности по модулю.
Абсолютная погрешность (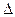 ) - модуль разности точного и приближенного значений искомой величины.
) - модуль разности точного и приближенного значений искомой величины.

!!! Чем меньше абсолютная погрешность, тем ближе приближенное значение к точному.
Если 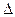 не превосходит некоторого числа h, то h называется границей абсолютной погрешности.
не превосходит некоторого числа h, то h называется границей абсолютной погрешности.
Границей абсолютной погрешности называется число h, удовлетворяющее неравенству:
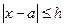 или
или 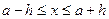 , т.е. большее или равное абсолютной погрешности.
, т.е. большее или равное абсолютной погрешности.
!!! Значение величины X с учетом погрешности записывается
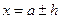
|
 - верхняя граница величины X;
- верхняя граница величины X;
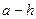 - нижняя граница величины X.
- нижняя граница величины X.
Двойной знак 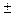 означает, что отклонение приближенного числа от точного возможно в обе стороны.
означает, что отклонение приближенного числа от точного возможно в обе стороны.
Пример 6 Найти границы числа x = 10,6 ± 0,5
Решение: 10,6 – 0,5 < x < 10,6 + 0,5
10,1< x < 11,1
Н.г. В.г.
В таблицах числовые значения приведены без указания погрешности, но так как эти числа округлены по основному правилу, то граница абсолютной погрешности каждого числа из таблиц равна половине единицы последнего разряда.
Пример 7 а) плотность меди равна 8,9± 0,05 г/см3;
б) теплота сгорания спирта равна 30±0,5 МДж/кг;
в) 
В качестве границы абсолютной погрешности берут по возможности меньшее число.
| Для упрощения терминологии, границу абсолютной погрешности иногда называют абсолютной погрешностью или просто погрешностью. В математике часто применяют выражения типа: «с точностью до 0,01», «с точностью до сантиметра» и т.п. при этом имеют в виду, что граница абсолютной погрешности соответственно равна 0,01; 1 см и т.д. |
|
2). Абсолютная погрешность не характеризует качество измерения.
3). Абсолютную погрешность применяют для сравнения точности приближенных значений величин одного порядка и одной размерности. Если приближенные значения величины существенно различны, то для сравнения их точности понятие абсолютной погрешности оказывается недостаточным.
Пример 8 Значение силы тока в одной лампочке 1±0,5 А, а в другой – 10 ± 0,5 А. Абсолютная погрешность обоих чисел одинаковы, однако совершенно очевидно, что погрешность 0,5 А при значении силы тока 1 А велика (50% измеряемой величины), для силы тока 10 А погрешность 0,5 А составляет лишь 5 %.
Для оценки качества измерения (вычисления) вводится относительная погрешность (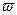 ).
).
Относительной погрешностью приближения называется отношение абсолютной погрешности приближения к модулю приближенного значения величины (или к модулю точного значения числа).

Относительную погрешность часто выражают в процентах:
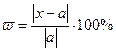
Так как точное значение числа, а, следовательно, и абсолютная погрешность чаще всего неизвестны, на практике приходится оценивать модуль относительной погрешности:
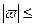 ε
ε
Можно взять ε 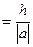 . Это число называется границей относительной погрешности.
. Это число называется границей относительной погрешности.
|
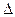 - абсолютная погрешность;
h – граница абсолютной погрешности; - абсолютная погрешность;
h – граница абсолютной погрешности;

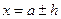

| 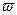 - относительная погрешность;
ε - граница относительной погрешности; - относительная погрешность;
ε - граница относительной погрешности;
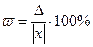 ε
ε 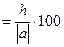 %
ε %
ε 
|
Пример 9 Сравнить качества измерений толщины книги d (см) и высоты стола H (см), если известно, что d = 2±0,5; H=100±0,5.
Решение: Для сравнения качества измерений найдем относительную погрешность каждого измерения:
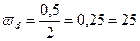 %;
%; 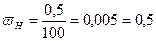 %
%
Итак, толщина книги измерена с относительной
погрешностью до 25%, а высота стола - до 0,5%. Качество измерений высоты стола намного лучше качества измерения толщины книги.
Пример 10 В лабораторной работе по определению ускорения свободного падения студент получил результат g = 1005 см/с2. Сравним это число с табличным:

Таким образом, относительная погрешность значения ускорения свободного падения равна 2,4%.
Пример 11 Пусть 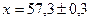 Вычислить границу относительной погрешности.
Вычислить границу относительной погрешности.
Дано: 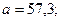 h=0,3
h=0,3
Найти: ε
Решение: ε 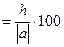 %; ε
%; ε 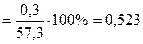 %.
%.
Пример 12 Установите, какое из приближений точнее:
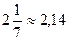 или
или 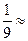 0,11
0,11
Дано: 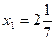 ,
, 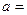 2,14
2,14
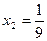 ,
, 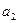 = 0,11
= 0,11
Найти: 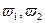 .
.
Решение: 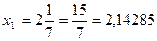 …,
…, 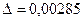 …, h=0,003, тогда
…, h=0,003, тогда 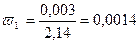 или 0,14%
или 0,14%
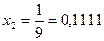 …,
…, 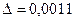 …, h=0,001 тогда
…, h=0,001 тогда
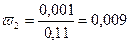 или 0,9%
или 0,9%
Итак: 0,14%<0,9%
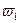 <
< 
Ответ: Первое приближение точнее.
Пример 13 Найти верхнюю и нижнюю границы приближенного числа 23,54, если граница относительной погрешности составляет 15%.
Дано: 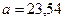 ; ε = 15%=0,15
; ε = 15%=0,15
Найти: Н.г. и В.г.
Решение: ε 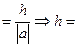 ε
ε 
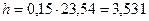 ;
; 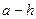 < x <
< x < 
Н.г.: 23,54-3,531=20,009
В.г.: 23,54+3,531=27,071
20,009 < x < 27,071
Н.г. В.г.
Выполните задания:
1. Округлите число 73,1729 до тысячных, сотых, десятых, единиц, десятков, сотен.
2. Найдите абсолютную погрешность приближенного равенства 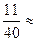 0,27.
0,27.
3. Округлите число до единиц и найдите абсолютную и относительную погрешность округления: а) 10,59; б) 0,892.
4. Число 1376 округлено до 1400. Найдите абсолютную и относительную погрешности округления.
5. Табличное значение плотности золота равно 19,3 г/см3. Найдите абсолютную и относительную погрешности этого значения.
6. Брусок имеет размеры 10*20*40 мм. Абсолютная погрешность каждого размера равна 0,5 мм.
Какова относительная погрешность каждого размера?
7. Найдите относительную погрешность приближения:
а) числа 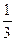 числом 0,33;
числом 0,33;
б) числа 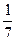 числом 0,14.
числом 0,14.
8. Вычислите границу относительной погрешности приближенных чисел:
а) 25,132±0,00052
б) 0,087±0,04
в) 5,7±0,1.
9. Скорость света в вакууме равна 299792,5±0,4 км/с, а скорость звука в воздухе – 331,63±0,04 м/с. Что измерено с большей точностью?
10. Длина отрезка при измерении с точностью до десятых дециметра равна 1,8 дм, при измерении с точностью до миллиметра – 180 мм. Во сколько раз второе измерение точнее первого?
11. Приближенное значение массы Земли равно (5,98±0,01) 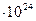 кг. Масса пули охотничьего ружья равна (9±1) г. Какое измерение является более точным?
кг. Масса пули охотничьего ружья равна (9±1) г. Какое измерение является более точным?
12. Установите, какое равенство точнее:
а) 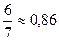 или
или 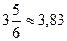
б) 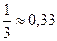 или
или 
в) 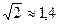 или
или 
13. Найдите нижнюю и верхнюю границы числа, если приближенное значение и относительная погрешность соответственно равны:
а) 2,45 и 7%
б) 54 и 3%
в) 0,4 и 25%
- Значащие, верные и сомнительные цифры приближенного значения числа
В книге В.М. Брадиса «Средства и способы элементарных вычислений» дало следующее определение значащих цифр: «Значащими цифрами числа называются все его цифры, кроме нулей, стоящих левее первой, отличной от нуля цифры, и нулей, стоящих в конце числа, если они стоят взамен неизвестных и отброшенных цифр».
. . . .
Пример 1 а) 3564 – четыре значащих цифры.
...
0,256 – три значащих цифры.
. ..
0,0302 – три значащих цифры.
1520 - четыре, если число записано с точностью до
единиц и три, если число записано с точностью до
десятков.
б) электрохимический эквивалент водорода 0,01045 мг/Кл. В этом числе четыре значащие цифры;
в) теплота сгорания дров 8300 кДж/кг. Если это число задано с точностью до сотен, то два нуля незначащие (поставлены взамен неизвестных цифр);
г) удельное сопротивление цинка 0,060 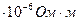 . Это число задано с точностью до тысячных, поэтому последний нуль значащий; в числе две значащие цифры.
. Это число задано с точностью до тысячных, поэтому последний нуль значащий; в числе две значащие цифры.
Отметим, что нуль, записанный в конце десятичной дроби, - всегда значащая цифра (иначе этот нуль просто не писали бы). Так, в числе
20,40 м, полученном в результате измерения с точностью до сантиметров, четыре значащие цифры. При этом важно обратить внимание на то, что равенство 20,40 м = 20,4 м, безусловно, правильное
для точных значений чисел, не является правильным для приближенных значений. Дело в том, что число 20,4 задано с точностью до десятых, а число 20,40 – с точностью до сотых.
Приведенное равенство является примером характерной ошибки студентов, склонных в ряде случаев применять известные им свойства точных значений чисел к приближенным значениям.
Рассмотрим целое приближенное значение с нулями справа. При определении количества значащих цифр этот случай наиболее сложный, так как нуль в конце целого числа может быть в одних случаях значащей цифрой, в других – незначащей.
Например, число 3500, заданное с точностью до единиц, имеет четыре значащие цифры. Если же то же число задано с точностью до сотен, то нули справа не будут значащими цифрами, и число 3500 будет иметь всего две значащие цифры.
Более того, возможен и такой случай, когда в одном и том же целом числе некоторые нули справа являются значащими, а некоторые – нет. Например, в значении скорости света с = 300 000 км/с первые три цифры (3,0,0) значащие; последние три (нули) – незначащие. Дело в том, что более точно скорость света равна 299793 км/с, что после округления до тысяч 299793 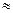 300 000 км/с дает погрешность, приближенно равную 200 км/с.
300 000 км/с дает погрешность, приближенно равную 200 км/с.
Как же записывать незначащие нули? Незначащие нули в конце целого приближенного числа можно отмечать знаком: ~. Например, в числе 800 первый нуль значащий, второй – незначащий. (Применение указанного условного обозначения (~) для незначащих нулей не является общепринятым, но введение его в некоторых случаях целесообразно, и мы им будем пользоваться на аудиторных занятиях).
Можно вообще не записывать незначащие нули. Для этого существует два способа:
 |
|
Пример 2 Приведем ряд примеров физических величин, записанных в стандартной форме:
| №n/n | Физические величины | Стандартная форма записи |
| 1. | Плотность воздуха | 1,29 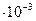 г/см3 г/см3
|
| 2. | Скорость света в вакууме | 3,00 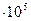 км/с км/с
|
| 3. | Масса Земли | 5,98 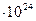 кг кг
|
| 4. | Постоянная Фарадея | 9,65 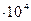 Кл/моль Кл/моль
|
| 5. | Постоянная Авогадро | 6,02 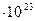 моль-1 моль-1
|
| 6. | Заряд электрона | 1,6 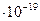 Кл Кл
|
Замечание: Рассмотренные способы позволяют, как правило, отказаться от записи незначащих нулей в конце целых приближенных чисел; если же нули сохранены, следует считать их значимыми.
Рассмотрим классификацию значащих цифр приближенного значения числа, играющую важную роль в приближенных вычислениях.
Если абсолютная погрешность приближенного числа не превышает единицы последнего разряда, то все значащие цифры приближенного числа называют верными.
Пример 3 а) плотность ртути равна 135955 г/см3. Округлим это значение до сотых: 13,60 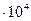 г/см3. Все цифры числа 13,60 верные, т.к. абсолютная погрешность округления равные 13,60 – 13,5955 = 0,0045, что меньше 0,01;
г/см3. Все цифры числа 13,60 верные, т.к. абсолютная погрешность округления равные 13,60 – 13,5955 = 0,0045, что меньше 0,01;
б) при измерении длины стержня линейкой с ценой деления 1 мм абсолютная погрешность не превышает 0,5 мм. Поэтому в результате измерения (56±0,5мм) обе цифры верные;
в) длина рулона обоев 10,5±0,05 м – все цифры (1,0,5) – верные.
г) в числе  =27,4±0,08 все цифры верные т.к. абсолютная погрешность 0,08<0,1.
=27,4±0,08 все цифры верные т.к. абсолютная погрешность 0,08<0,1.
Иногда при измерениях и, особенно при вычислениях, результат может иметь погрешность, превышающую единицу последнего разряда. Например, при измерении объема жидкости мензуркой с ценой деления 10 мл получен результат 120±5 мл. Цифра 0 в числе 120 не является верной, так как абсолютная погрешность больше единицы последнего разряда. В подобных случаях последняя цифра приближенного числа сомнительная.
Если в приближенном числе все значащие цифры, кроме последней, являются верными, но абсолютная погрешность числа превышает единицу последнего разряда, то цифру этого разряда называют сомнительной.
Пример 4 x=75,3±0,2
Здесь цифры 7 и 5 – верные, цифра 3 – сомнительная, т.к. h > 0,1
|
1) Если в десятичной дроби последние верные цифры – нули, то их оставляют в записи числа.
Например, если 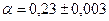 , то правильная запись числа есть 0,230.
, то правильная запись числа есть 0,230.
2) Если в целом числе последние нули являются сомнительными цифрами, то их исключают из записи числа.
Например, если 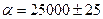 , то правильная запись числа есть
, то правильная запись числа есть 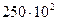 или
или 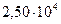 .
.
3) В записи числа 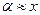 последняя цифра десятичной записи числа указывает на точность приближения, т.е. граница абсолютной погрешности не превосходит единицы последнего разряда.
последняя цифра десятичной записи числа указывает на точность приближения, т.е. граница абсолютной погрешности не превосходит единицы последнего разряда.
Например, запись числа 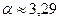 означает, что
означает, что 
| Мы будем пользоваться правилом записи приближенных значений чисел, предложенным В.М. Брадисом: в приближенных значениях чисел, полученных в результате измерения или вычисления, сохраняют все верные цифры и, возможно, одну сомнительную, если известно, что малые значения погрешности более вероятны, чем большие. |
Выполните задания:
1. В таблице приведены плотности некоторых веществ. Сколько значащих цифр в каждом числе?
| № n/n | Вещество | Плотность, г/см3 |
| Вода | 1,00 | |
| Спирт | 0,80 | |
| Молоко | 1,03 | |
| Ртуть | 13,60 | |
| Глицерин | 1,26 |
2. В наборе имеются гири: 500 г., 200 г., 100 г. и 50 г. Какие нули в этих числах значащие или незначащие?
3. Не изменяя точности чисел, запишите:
а) 170 мм в сантиметрах;
б) 250 мл в литрах;
в) 600 В в киловольтах.
4. Округлите следующие числа:
а) до двух значащих цифр: 7,82; 7,98; 1,96; 1,00; 0,032;
0,999;
б) до трех значащих цифр: 87856; 19,995; 78,625; 0,006798; 0,1199;
в) до четырех значащих цифр: 60002480; 87,99567; 0,000678078; 0,007800456; 0,00679987.
5. В следующих числах последний нуль справа незначащий. Путем перехода к кратным единицам запишите эти числа без незначащих нулей: 200 см, 1400 м, 1500 мл, 60 Н, 220 В, 4500 Ом.
6. В следующих числах все нули справа незначащие. Путем перехода к кратным единицам запишите эти числа без незначащих нулей: 7800 Дж, 9200000 Дж, 6600000 Ом, 1 120 000 кВт.
7. Следующие числа выразите в единицах СИ и подсчитайте число незначащих нулей: 12 км, 0,050 км2, 50,0 m, 1,60 МН, 6,60 кВ.
8. Теплота сгорания торфа равна 1500 кДж/кг, спирта – 30 000 кДж/кг, бензина – 46 200 кДж/кг. Числа даны с точностью до сотен. Сколько значащих цифр в каждом числе? Запишите числа в стандартной форме.
9. Заполните таблицу:
| № n/n | Вещество | Плотность вещества, г/см3 | |
| Данное значение | Стандартная форма | ||
| Азот | 0,00125 | ||
| Гелий | 0,00018 | ||
| Водород | 0,00009 |
10. Показания счетчика электроэнергии в начале и в конце срока измерения следующие:
Одна цифра справа – десятые доли киловатт-часа.
а) Сколько значащих цифр в каждом числе? Какие из них являются верными?
б) Ответьте на те же вопросы, если десятые доли киловатт-часа принято отбрасывать без округления.
11. Сколько верных цифр имеет число:
а) 5,74 ± 0,01
б) 1,174 ± 0,025
в) 0,874 ± 0,05
12. Округлите приближенное значение числа x до первого верного разряда:
а) x = 0,2391 ± 0,05
б) x = 1,0738 ± 0,0025
в) x = 2354 ± 50
13. Показатель преломления бензина равен n = 1,5014 ± 0,0002. Сколько в этом числе верных и сомнительных цифр?
14. Постоянная Фарадея F = 9,65 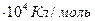 имеет границу абсолютной погрешности
имеет границу абсолютной погрешности 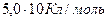 . Сколько в этом числе верных и сомнительных цифр?
. Сколько в этом числе верных и сомнительных цифр?
15. Результаты двух лабораторных работ были записаны так: ρ = 7,48 ± 0,2 г/см3;
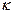 = 0,322 ± 0,01 мг/Кл.
= 0,322 ± 0,01 мг/Кл.
Запишите результат верными цифрами.
16. Число 3000 ± 100 разные студенты записали так:
3,0 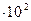 ;
; 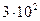 ; 30
; 30 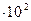 .
.
Верна ли каждая из этих записей?
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 11726; Нарушение авторских прав?; Мы поможем в написании вашей работы!