Нечетко-интервальные модели

Задача достижения нечетко определенной цели

(подход Беллмана-Заде)

Основным в данном подходе к решению рассматриваемой задачи является то, что цели принятия решений и множество альтернатив рассматриваются как равноправные нечеткие подмножества некоторого универсального множества альтернатив. Это позволяет определить решение задачи в относительно простой форме.

Пусть Х – универсальное множество альтернатив, т.е. универсальная совокупность всевозможных выборов лица, принимающего решения (ЛПР). Нечеткой целью является нечеткое подмножество X, которое мы будем обозначать G. Описывается нечеткая цель функцией принадлежности m _G: X ® [0,1]. Нечетким ограничением является нечеткое подмножество X, которое мы будем обозначать С. Описывается нечеткое ограничение функцией принадлежности m _С: X ® [0,1].

Чем больше степень принадлежности альтернативы x нечеткому множеству цели m _G, т.е. чем больше значение m _G (x), тем больше степень достижения этой цели при выборе альтернативы x в качестве решения. То же самое можно сказать и относительно ограничений.

Решить задачу – означает достигнуть цели и удовлетворить ограничениям, причем в данной нечеткой постановке следует говорить не просто о достижении цели, а об ее достижении с той или иной степенью, причем следует учитывать и степень выполнения ограничений.

В подходе Беллмана-Заде оба эти фактора учитываются следующим образом. Пусть, например, некоторая альтернатива x обеспечивает достижение цели (или соответствует цели) со степенью m _G (x), удовлетворяет ограничениям (или является допустимой) со степенью m _С (x).

Тогда полагается, что степень принадлежности этой альтернативы решению задачи равна минимальному из этих чисел. Иными словами, альтернатива, допустимая со степенью, например, 0.3, с той же степенью принадлежит нечеткому решению, несмотря на то, что она обеспечивает достижение цели со степенью, равной, например, 0.8.

Таким образом, нечетким решением задачи достижения нечеткой цели называется пересечение нечетких множеств цели и ограничений, т.е. тоже нечеткое множество D, функция принадлежности которого m _D имеет вид: m _D (x)= min {m _G (x),m _C (x)}.

При наличии нескольких целей и ограничений нечеткое решение описывается функцией принадлежности:

m _D (x)= min {m _{G 1} (x),¼,m _Gn (x), m _{C 1} (x), ¼,m _Cn (x)}.

Оптимальной в смысле подхода Беллмана-Заде будет альтернатива х *, для которой m _D (x)максимальна:

х*: m _D (x*) =max m _D (x).

x Î X

До сих пор предполагалось, что все цели и ограничения, входящие в нечеткое множество решений D, имеют одинаковую важность. Более привычная ситуация, в которой удовлетворение одним целям и (или) ограничениям, важнее, чем другим. Обозначим через коэффициент относительной важности i -ой цели, а через – коэффициент относительной важности j -го ограничения, причем 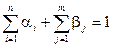. Тогда функцию принадлежности решения можно определить так:

m _D (x) = min {[m _{G 1} (x)]^α1,¼,[m _Gn (x)]^αn, [m _{C 1} (x)]^β1, ¼,[m _Cn (x)] ^{β m} }. (2)

Чем меньше коэффициент относительной важности, тем соот-ветствующее нечеткое множество цели или ограничения стано-вится более размазанным, и, следовательно, его роль в принятии решения снижается.

Рассмотрим пример. Нечеткая цель G и нечеткое ограничение C сформулированы так:

G: «x должно быть около 10» и

C: «x должно быть значительно больше 8».

Функции принадлежности нечетких множеств G и C заданы выражениями

, .

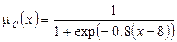Необходимо найти нечеткое решение D.

Учитывая, что пересечению нечетких множеств соответствует операция минимума над функциями принадлежности, получаем:

Взаимосвязь между нечеткими целью, ограничением и решением показана на рис. 9. Цель и ограничения конфликтуют между собой, поэтому в нечетком множестве D нет ни одного элемента со степенью принадлежности, равной 1. Значит, не существует альтернативы, которая полностью удовлетворяет и цели, и ограничению. В качестве четкого решения в таких случаях обычно выбирают альтернативу с максимальной степенью принадлежности нечеткому множеству D.

Рис. 9. К примеру «Принятие решения по принципу Беллмана-Заде»

При принятии решений по схеме Беллмана-Заде не делается никакого различия между целью и ограничениями. Всякое разделение на цель и ограничения является условным: в формуле (2) можно поменять местами цель с ограничением, при этом решение не изменится.

На рис. 10 приведены нечеткие решения при различных коэф-фициентах важности цели и ограничения из предыдущего примера.

Рис. 10. К примеру принятия решений при разной важности цели и ограничения

Дата добавления: 2014-12-27