Введение. Психология девиантного развития и поведения

Психология девиантного развития и поведения

учебно-методическое пособие

для бакалавров педагогики очной и заочной форм обучения

Появление и непрерывное совершенствование быстродействующих электронных вычислительных машин (ЭВМ) привело к подлинно революционному преобразовании науки вообще и математики в особенности. Решение крупных научно-технических проблем, примерами которых могут служить проблемы овладения ядерной энергией и освоения космоса, стало возможным лишь благодаря применению математического моделирования и новых численных методов, предназначенных для ЭВМ.

Подобные задачи решаются на основе математического описания (математической модели) естественных процессов и последующего решения соответствующих математических задач на ЭВМ при помощи вычислительных алгоритмов.

Разработка и исследование вычислительных алгоритмов и их применение к решению конкретных задач составляет содержание огромного раздела современной математики – вычислительной математики.

Вычислительную математику в широком смысле этого термина определяют как раздел информатики, включающий круг вопросов, связанных с использованием ЭВМ, и в узком смысле – как теорию численных методов и алгоритмов решения поставленных математических задач. В дальнейшем вычислительную математику мы будем рассматривать именно исходя из второго определения.

Общим для всех численных методов является сведение математической задачи к конечномерной. Это чаще всего достигается дискретизацией исходной задачи, т.е. переходом от функций непрерывного аргумента к функциям дискретного аргумента. После дискретизации исходной задачи надо построить вычислительный алгоритм, т.е. указать последовательность арифметических и логических действий, выполняемых на ЭВМ и дающих за конечное число действий решение дискретной задачи. Полученное решение дискретной задачи принимается за приближенное решение исходной математической задачи.

При решении задачи на ЭВМ мы всегда получаем не точное решение исходной задачи, а некоторое приближенное. Это обусловлено тем, что во-первых входные (исходные) данные исходной задачи всегда задаются с некоторой погрешностью, во-вторых при замене исходной задачи дискретной возникает погрешность, в-третьих конечная разрядность чисел, представляемых в ЭВМ, также приводит к погрешности, которую называют погрешностью округления. В процессе решения задачи эти погрешности могут нарастать.

Погрешности округления появляются на каждом этапе вычисления. В зависимости от алгоритма эти погрешности могут либо нарастать, либо затухать. Если в процессе вычислений погрешности округления неограниченно нарастают, то такой алгоритм называют неустойчивым. Если же погрешности округления не накапливаются, то алгоритм является устойчивым.

Для каждой задачи ставятся одни и те же вопросы: существует ли решение задачи, является ли оно единственным и как зависит решение от входных данных? Возможны два случая:

ü Задача поставлена корректно (задача корректна); это значит, что 1) задача разрешима при любых допустимых входных данных; 2) имеется единственное решение; 3) решение задачи непрерывно зависит от входных данных (малому изменению входных данных соответствует малое изменение решения) – иными словами, задача устойчива.

ü Задача поставлена некорректно (задача некорректна), если ее решение неустойчиво относительно входных данных (малому изменению входных данных может соответствовать большое изменение решение).

Примером корректной задачи может служить задача интегрирования, а примером некорректной задачи – задача дифференцирования.

В данном пособие мы будем рассматривать только корректные задачи и корректные численные методы, ориентированные на использование ЭВМ.

В 1-ой главе рассматриваются основные вопросы теории погрешностей, а именно, вопрос классификации погрешностей и вопрос оценки погрешности округления. В 1-ом параграфе проведена классификация погрешностей. Во 2-ом параграфе этой главы представлены основные понятия и утверждения теории погрешностей – абсолютная и относительная погрешность, правила округления чисел, верные и сомнительные цифры приближенного числа, правила выполнения операций над приближенными числами, правила округления результатов этих операций.

Во 2-ой главе излагаются численные методы решения нелинейных уравнений. Первый параграф этой главы посвящен вопросу отделения корней и уточнению промежутков изоляции корня. На конкретном примере в нем разобрано практическое применение теоретического материала.

Во 2-ом параграфе 2-ой главы рассматриваются приемы контроля точности приближенного значения корня и четыре численных метода решения нелинейного уравнения 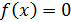– метод вилки, метод хорд, метод касательных и метод итерации. Так же здесь приведены алгоритмы перечисленных методов, показан вывод формул данных методов, сформулирована теорема о сходимости метода итерации и приведена геометрическая иллюстрация этого метода. Кроме этого в нем подробно разобраны примеры решения алгебраических и неалгебраических уравнений всеми четырьмя методами, причем каждым из рассмотренных методов прорешены одни и теже уравнения. Это сделано для того чтобы можно было сравнить эффективность рассмотренных численных методов.

В 3-ем параграфе 2-ой главы проведен анализ эффективности всех четырех методов исходя из их универсальности, простоты организации вычислительного процесса и контроля точности, скорости сходимости и количества арифметических операций требуемых для вычисления корней.

В 3-ей главе излагаются методы интерполирования и приближения (аппроксимации) функций.

В 1-ом параграфе 3-ей главы рассмотрены общие понятия теории интерполяции (интерполяционная функция, узлы интерполяции, интерполяционный многочлен и остаточный член (погрешность) интерполяционной функции), приведены формулы интерполяционных многочленов Лагранжа и Ньютона и соотношение для оценки погрешности интерполирования. Так же в это параграфе подробно разобраны примеры построения интерполяционных многочленов Лагранжа и Ньютона, их применения для вычисления приближенных значений интерполируемой функции в точках, отличных от узлов интерполирования.

2-ой параграф 3-ей главы посвящен изложению общей теории аппроксимации функции, а именно, вопросам решения задачи о нахождении наилучшего среднеквадратичного приближения.

В 4-ой главе излагаются вопросы численного решения систем линейных алгебраических уравнений и систем нелинейных уравнений. Для решения систем уравнений применяются прямые и итерационные методы.

В 1-ом параграфе 4-ой главы рассматриваются прямые (точные) методы решения систем линейных алгебраических уравнений – метод Крамера, метод Гаусса и метод прогонки. При изложении материала о методе Гаусса представлен общий алгоритм решения систем, проанализирован вопрос устойчивости метода к ошибкам округления и способ нивелирования этих ошибок, который называется выбором ведущего элемента по строке, показано практическое применение метода Гаусса на конкретных примерах. При изучении метода прогонки рассматриваются область применения метода и его устойчивость к ошибкам округления, а так же рекуррентные соотношения для определения прогоночных коэффициентов и нахождения неизвестных, и приведены примеры применения метода прогонки на конкретных примерах.

Во 2-ом параграфе 4-ой главы рассматриваются итерационные методы решения систем линейных алгебраических уравнений – метод простой итерации и метод Зейделя. При изучении итерационных методов важную роль играет каноническая форма записи итерационного метода. При этом предполагается, что матрица системы самосопряженная и положительно определенная. Здесь же представлены различные формы записи метода простой итерации и метода Зейделя, сформулировано достаточное условие сходимости итерационных методов, на основе которого доказаны условия сходимости метода простой итерации и метода Зейделя, а так же проанализированы вопросы скорости сходимости этих методов. Кроме этого в параграфе подробно разобраны примеры применения итерационных методов для решения систем линейных уравнений.

В 3-ем параграфе 4-ой главы изложены вопросы решения систем нелинейных уравнений итерационными методами, на примере, метода Ньютона и сформулирован принцип сжимающих отображений для систем уравнений.

В 5-ой главе исследованы вопросы приближенного вычисления определенных интегралов. Первый параграф содержит общие понятия теории численного интегрирования, такие как квадратурная формула, погрешность квадратурной формулы, сходимость и точность квадратурной формулы.

Во 2-ом параграфе 5-ой главы представлены вывод квадратурной формулы прямоугольников, ее геометрический смысл, исследование сходимости и способ оценки погрешности квадратурной формулы. Так же этот параграф содержит подробно разобранные примеры применения квадратурной формулы прямоугольников.

В 3-ем параграфе 5-ой главы изложены вывод квадратурной формулы трапеций, ее геометрический смысл, исследование сходимости и способ оценки погрешности квадратурной формулы. Так же этот параграф содержит подробно разобранные примеры применения квадратурной формулы трапеций.

В 4-ом параграфе 5-ой главы рассмотрены вывод квадратурной формулы Симпсона (парабол), исследование ее сходимости и способ оценки погрешности квадратурной формулы. Так же этот параграф содержит подробно разобранные примеры применения квадратурной формулы Симпсона.

В 5-ом параграфе 5-ой главы изложены вопросы апостериорной оценки погрешности квадратурных формул, представлены формулы для апостериорной оценки этих формул и разобран пример на определение апостериорной оценки погрешности.

В конце параграфов, за исключением 1-го параграфа 1-ой главы, 3-го параграфа 2-ой главы, 2-го параграфа 3-ей главы, 3-го параграфа 4-ой главы и 5-го параграфа 5-ой главы представлены упражнения по соответствующим темам для самостоятельной работы студентов.

Глава 1. Погрешность численного решения.

Практическая деятельность человека неразрывно связана с числами, которые можно получать тремя способами: в результате измерений, счета и выполнения различных математических операций. Однако необходимо заметить, что:

1. любое измерение нельзя выполнить абсолютно точно (ошибку дает либо сам прибор, либо наблюдатель);

2. счет дает точные результаты, только если количество пересчитываемых предметов невелико и если оно постоянно во времени;

3. далеко не все математические операции можно выполнить абсолютно точно (вычисление квадратного корня из 2 – 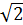≈ 1,4).

Поэтому первым в теории численных методов является вопрос о классификации и способах определения погрешности числа и приемах определения погрешности вычислений, полученных в процессе арифметических операций с приближенными числами.

Дата добавления: 2014-12-27