
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод итерации (последовательных приближений)
|
|
|
|
Метод касательных (метод Ньютона).
Шаг.
Шаг.
Шаг.

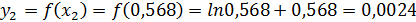 .
.
Составим разность 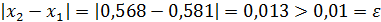 . Так как
. Так как  , то требуемая точность не достигнута и процесс нахождения приближенного значения корня уравнения (2).
, то требуемая точность не достигнута и процесс нахождения приближенного значения корня уравнения (2).
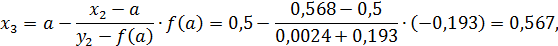
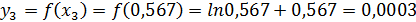 .
.
Составим разность 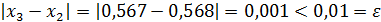 . Так как
. Так как 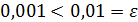 , то требуемая точность достигнута и процесс нахождения приближенного значения корня уравнения (2) закончен.
, то требуемая точность достигнута и процесс нахождения приближенного значения корня уравнения (2) закончен.
Следовательно, с точностью до 0,01 приближенное значение корня уравнения (2) х*= 0,567.
Ответ. 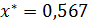 с точностью до ε= 0,01.
с точностью до ε= 0,01.
Пример 2. Методом хорд найти приближенное значение положительного действительного корня уравнения 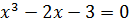 с точностью до ε= 0,01.
с точностью до ε= 0,01.
Решение.
1 этап. Отделим корни уравнения 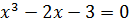 . В примере 2 п. 2.2.1. было показано, что точное значение положительного корня х* данного уравнения лежит на отрезке [1,8; 2].
. В примере 2 п. 2.2.1. было показано, что точное значение положительного корня х* данного уравнения лежит на отрезке [1,8; 2].
2 этап. Рассмотрим функцию  и найдем её первую и вторую производные. Так как
и найдем её первую и вторую производные. Так как 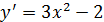 ,
,  и
и  ,
, 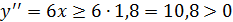 при х
при х  [1,8; 2], то вычисление приближенного значения корня будем проводить по формулам (4).
[1,8; 2], то вычисление приближенного значения корня будем проводить по формулам (4).
1 шаг. Так как
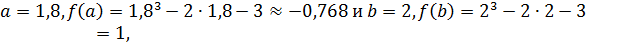
то в результате имеем:
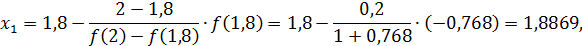
 .
.

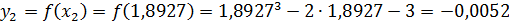 .
.
Составим разность  то требуемая точность достигнута и процесс нахождения приближенного значения корня уравнения
то требуемая точность достигнута и процесс нахождения приближенного значения корня уравнения 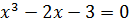 закончен.
закончен.
Следовательно, с точностью до 0,01 приближенное значение корня данного уравнения х*= 1,8927.
Ответ.  с точностью до ε= 0,01.
с точностью до ε= 0,01.
Пусть на отрезке [ a; b ] функция f(x) непрерывна и дважды дифференцируема, на концах отрезка принимает значения разных знаков, т. е. f(a)f(b)< 0,  и
и  не обращаются в ноль не в одной точке. Тогда уравнение (1) на отрезке [ a; b ] имеет единственное действительное решение х*, приближенное значение которого можно найти, используя метод касательных (метод Ньютона).
не обращаются в ноль не в одной точке. Тогда уравнение (1) на отрезке [ a; b ] имеет единственное действительное решение х*, приближенное значение которого можно найти, используя метод касательных (метод Ньютона).
Изобразим схематически графики четырех типов расположения дуги функции f (x) на отрезке [ a; b ] (рис. 9 – 12).
|
|
|
| А |
| Рисунок 9 |
| В |
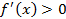
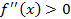
|
| х |
| у |
| О |
| а |
| х * |
| х 1 |
| х 2 |
| х 3 |
| b |
| В 1 |
| В 2 |
| В 3 |
| А |
| х 1 |
| х 2 |
| х * |
| А 1 |
| А 2 |
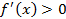

|
| Рисунок 10 |
| х |
| у |
| О |
| а |
| b |
| В |
| Рисунок 12 |
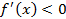

|
| х |
| у |
| О |
| а |
| А |
| В |
| b |
| В 1 |
| В 2 |
| х * |
| х 1 |
| х 2 |
| А |
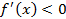
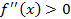
|
| Рисунок 11 |
| х |
| у |
| О |
| b |
| х * |
| х 2 |
| А 1 |
| а |
| х 1 |
| х 3 |
| А 2 |
| А 3 |
| В |
Рассмотрим два случая: 1) 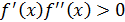 ; 2)
; 2) 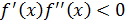 .
.
1 случай. 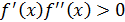 на [ a; b ], т. е. либо
на [ a; b ], т. е. либо 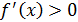 и
и  на [ a; b ] (см. рис. 9), либо
на [ a; b ] (см. рис. 9), либо 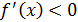 и
и 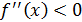 на [ a; b ] (см. рис. 12).
на [ a; b ] (см. рис. 12).
Построим алгоритм нахождения приближенного значения корня уравнения (1) в данном случае.
1 шаг. Через точку B (b; f (b)) проведем касательную к графику функции y=f (x), уравнение которой имеет вид:
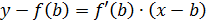 или
или

Положив у= 0, найдем абсциссу 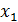 точки пересечения касательной с осью Ох:
точки пересечения касательной с осью Ох:
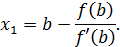
Подставив значение 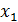 в уравнение графика функции y=f (x), найдем значение:
в уравнение графика функции y=f (x), найдем значение: 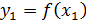 . Обозначим через В 1 точку с координатами
. Обозначим через В 1 точку с координатами 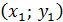 , т. е. В 1
, т. е. В 1 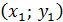 .
.
2 шаг. Через точку В 1 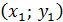 проведем касательную к графику функции y=f (x), уравнение которой имеет вид:
проведем касательную к графику функции y=f (x), уравнение которой имеет вид:
 или
или

Положив у= 0, найдем абсциссу 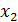 точки пересечения касательной с осью Ох:
точки пересечения касательной с осью Ох:
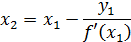
Подставив значение 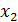 в уравнение графика функции y=f (x), найдем значение:
в уравнение графика функции y=f (x), найдем значение: 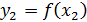 . Обозначим через В 2 точку с координатами
. Обозначим через В 2 точку с координатами  , т. е. В 2
, т. е. В 2  .
.
3 шаг. Через точки В 2  проведем касательную к графику функции y=f (x), уравнение которой имеет вид:
проведем касательную к графику функции y=f (x), уравнение которой имеет вид:
 или
или
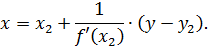
Положив у= 0, найдем абсциссу 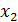 точки пересечения касательной с осью Ох:
точки пересечения касательной с осью Ох:

И так далее.
В результате получим последовательность 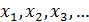 , сходящуюся к точному значению корня х* уравнения (1). Процесс построения последовательности
, сходящуюся к точному значению корня х* уравнения (1). Процесс построения последовательности 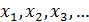 , т. е. нахождения приближенного значения корня уравнения (1) с заданной точностью
, т. е. нахождения приближенного значения корня уравнения (1) с заданной точностью 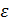 заканчиваем после выполнения неравенства
заканчиваем после выполнения неравенства 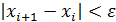 .
.
|
|
|
| (6) |
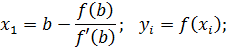

где i= 1, 2, 3, ….
2 случай. 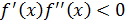 на [ a; b ], т. е. либо
на [ a; b ], т. е. либо 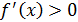 и
и 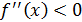 на [ a; b ] (см. рис. 10), либо
на [ a; b ] (см. рис. 10), либо 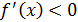 и
и  на [ a; b ] (см. рис. 11).
на [ a; b ] (см. рис. 11).
Алгоритм решения задачи в этом случае будет таким же, как и в первом случае, только первая касательная будет проводиться через точку A (a; f (a)) графика функции y=f (x).
А вычисления в этом случае будут проводиться по формулам:

| (7) |
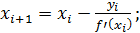
где i= 1, 2, 3, ….
Пример 1. Методом касательных найти приближенные значения действительных корней уравнения 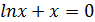 с точностью до ε= 0,01.
с точностью до ε= 0,01.
Решение.
1 этап. Уравнение 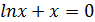 имеет единственный действительный корень х*, который расположен на отрезке [0,5; 1] (см. пример п. 2.1.).
имеет единственный действительный корень х*, который расположен на отрезке [0,5; 1] (см. пример п. 2.1.).
2 этап. Рассмотрим функцию  и найдем её первую и вторую производные. Так как
и найдем её первую и вторую производные. Так как 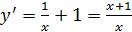 ,
, 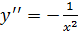 и
и  ,
, 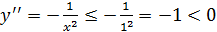 при х
при х  [0,5; 1], то вычисление приближенного значения корня будем проводить по формулам (7). Построим схематически график функции
[0,5; 1], то вычисление приближенного значения корня будем проводить по формулам (7). Построим схематически график функции  (рис. 13).
(рис. 13).
| -0,193 |
| х 1 |
| Рисунок 13 |
| х |
| у |
| О |
| х * |
| х 2 |
| А |
| 0,5 |
| А 1 |
| А 2 |
| В |
1 шаг. Координаты точки А (0,5; -0,193), следовательно,

В результате имеем:
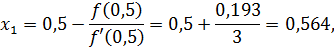

2 шаг. Так как 
 =2,773, то
=2,773, то

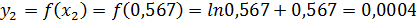 .
.
Составим разность  . Так как
. Так как 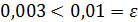 , то требуемая точность достигнута и процесс нахождения приближенного значения корня уравнения (2) закончен.
, то требуемая точность достигнута и процесс нахождения приближенного значения корня уравнения (2) закончен.
Следовательно, с точностью до 0,01 приближенное значение корня уравнения (2) х*= 0,567.
Ответ. 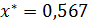 с точностью до ε= 0,01.
с точностью до ε= 0,01.
Пример 2. Методом касательных найти приближенное значение положительного действительного корня уравнения 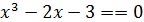 с точностью до ε= 0,01.
с точностью до ε= 0,01.
Решение.
1 этап. Отделим корни уравнения 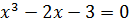 . В примере 2 п. 2.2.1. было показано, что точное значение положительного корня х* данного уравнения лежит на отрезке [1,8; 2].
. В примере 2 п. 2.2.1. было показано, что точное значение положительного корня х* данного уравнения лежит на отрезке [1,8; 2].
2 этап. Рассмотрим функцию  и найдем её первую и вторую производные. Так как
и найдем её первую и вторую производные. Так как 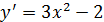 ,
,  и
и  ,
, 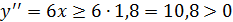 при х
при х  [1,8; 2], то вычисление приближенного значения корня будем проводить по формулам (6).
[1,8; 2], то вычисление приближенного значения корня будем проводить по формулам (6).
1 шаг. Координаты точки В (2; 1), так как
 .
.
В результате имеем:

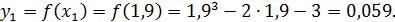
2 шаг. Так как  , то
, то
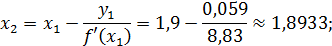
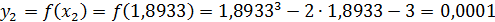 .
.
Составим разность 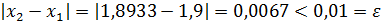 , то требуемая точность достигнута и процесс нахождения приближенного значения корня уравнения
, то требуемая точность достигнута и процесс нахождения приближенного значения корня уравнения 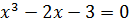 закончен.
закончен.
Следовательно, с точностью до 0,01 приближенное значение корня данного уравнения х*= 1,8933.
|
|
|
Ответ.  с точностью до ε= 0,01.
с точностью до ε= 0,01.
Предположим, что нам удалось найти достаточно малый промежуток [ a; b ]содержащий ровно один действительный корень уравнения (1), и что функция f (x) непрерывна и дифференцируема во всех точках данного промежутка.
Заменим уравнение (1) уравнением вида: х = φ (х), равносильным данному. Это всегда можно сделать и притом многими способами.
Так, например, уравнение 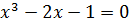 легко заменяется следующими равносильными уравнениями:
легко заменяется следующими равносильными уравнениями:
 (здесь
(здесь  );
);
 (здесь
(здесь  );
);
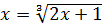 (здесь
(здесь  ).
).
Приведем без доказательства формулировку теоремы, определяющую условия применимости метода итераций.
Теорема. Если уравнение f(x)= 0 и равносильное ему уравнение х = φ (х) имеют ровно один действительный корень на промежутке [ a; b ] и, кроме этого, выполняются условия:
1) 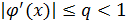 на [ a; b ];
на [ a; b ];
2)  на [ a; b ],
на [ a; b ],
то метод итераций имеет решение, причем в качестве начального приближения корня можно брать любое действительное значение х 0 из отрезка [ a; b ].
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 706; Нарушение авторских прав?; Мы поможем в написании вашей работы!