Заключительные замечания

Мы познакомились с четырьмя основными методами численного решения уравнений вида (1) – метод вилки (половинного деления), метод хорд, метод касательных (Ньютона) и метод итерации (последовательных приближений). Ситуация, когда одну и ту же математическую задачу можно решить с помощью различных методов, является типичной. В подобных случаях возникает необходимость сравнения их между собой.

При оценке эффективности численных методов существенное значение имеют следующие свойства: 1) универсальность; 2) простота организации вычислительного процесса и контроля точности; 3) скорость сходимости; 4) число арифметических операций требуемых для вычисления.

Рассмотрим с этой точки зрения разобранные методы решения уравнений (1).

1. Наиболее универсальным является метод вилки, так как он требует только непрерывности функции f (x). Остальные методы требуют более жестоких ограничений. Например, методы хорд и касательных требуют не только непрерывности а так же и дважды дифференцируемости функции f (x), а метод итерации требует не только непрерывности и дифференцируемости функции f (x), а так же выполнения условий теоремы (см. §2.2, п. 2.2.4). Во многих случаях это преимущество метода вилки может иметь существенное значение.

2. С точки зрения организации вычислительного процесса все четыре метода очень просты. Однако и здесь метод вилки обладает определенными преимуществами: вычисления можно начинать с любого отрезка [ a; b ], на концах которого функция f (x) принимает значения разных знаков и на котором она монотонна. Процесс будет сходиться к корню уравнения, причем на каждом шаге он дает двустороннюю оценку, по которой легко контролировать достигнутую точность. Сходимость остальных методов зависит от того, насколько удачно выбрано начальное приближение.

3. Наибольшей скоростью сходимости обладает метод касательных. В случае, когда подсчет значений функции f (x) сложен и требует существенных затрат машинного времени, это преимущество становится определяющим.

4. Во всех рассмотренных методах число требуемых для вычисления приближенного значения корня арифметических операций зависит от величины промежутка изоляции корня, особенно это фактор влияет на вычисления в методе вилки. В методах хорд, касательных и простой итерации эта характеристика зависит и от выбора начального приближения корня, чем точнее выбрано начальное приближение, тем меньше арифметических операций придется выполнять. Кроме этого в методе касательных приходится проводить дополнительные вычисления в отличии, например, от метода хорд, для определения значений производной.

Итак, мы видим, что ответ на вопрос о наилучшем численном методе решения уравнений (1) неоднозначен. Он существенно зависит от того, какую дополнительную информацию о функции f (x) мы имеем и в соответствии с этим каким свойствам метода придаем наибольшее значение.

Глава 3. Интерполирование и приближение функций.

В вычислительной практике часто встречаются функции, значения которых заданы лишь в нескольких различных точках отрезка [ a; b ]. Например, при обработке: результатов физического эксперимента; результатов статистического опроса; экономических данных и т. п. Как вы помните из школьного курса математики, подобные функции называются, заданными таблично. Пусть f (x) – такая функция, т. е. f (x_i) = у_i, i = 0, 1, 2, …, n или

Таблица 1

х	х 0	х 1	х 2	…	хn
f (x)	у 0	у 1	у 2	…	уn

Рассмотрим следующую задачу: по известным значениям функции f (x), заданной таблично (значения представлены в таблице 1) «восстановить», хотя бы приближенно, исходную функцию (доопределить функцию f (x) в остальных точках отрезка [ a; b ]). Для решения этой задачи необходимо построить на промежутке [ a; b ] функцию F (x), достаточно близкую к f (x) и такую что F (x_i) = f (x_i), i = 0, 1, 2, …, n. Функцию F (x) принято называть интерполирующей, точки 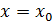, , 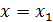…, 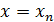– узлами интерполяции, а сам процесспостроения функции F (x) – интерполированием. Подобные задачи так же возникают, в случае, если требуется вычислить значения функции f (x) при значениях аргумента, не совпадающего ни с одним из табличных х_i.

Очевидно, в каждом конкретном случае существует бесконечно много вариантов построения функции F (x), поэтому к ней предъявляется ряд требований, наиболее важным из которых является простота вычисления этой функции. В этой главе мы рассмотрим два наиболее распространенных метода – интерполирование алгебраическими многочленами и методы наилучшего приближения.

Дата добавления: 2014-12-27