Системы с трехдиагональной матрицей. Метод прогонки

При решении многих практических задач приходится иметь с системами линейных уравнений вида

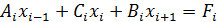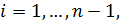, (36)

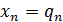, , (37)

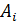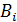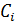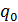где коэффициенты , , , правые части известны вместе с числами и 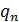. Дополнительные соотношения (37) часто называют краевыми условиями для системы (36).

Пользуясь тем, что значения 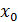и 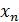заданы перепишем систему (36) в виде

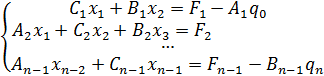. (38)

Матрица этой системы имеет трехдиагональную структуру:

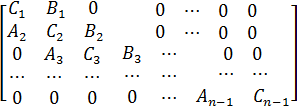. (39)

Системы вида (36) решают с помощью специального метода, который называется метод прогонки. Этот метод основан на предположении, что искомые неизвестные 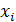и 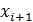связаны рекуррентным соотношением

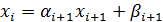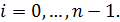, (40)

Величины и 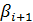, получившие название прогоночных коэффициентов определяются из условий задачи (36), (37).

Для определения прогоночных коэффициентов используют следующие рекуррентные соотношения:

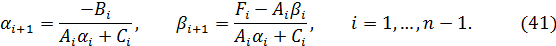
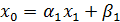Левое краевое условие и соотношение будут непротеворечивы, если положить

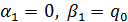. (42)

Остальные значения прогоночных коэффициентов и находим из равенств (41).

Далее, согласно правому краевому условию

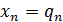. (43)

Отсюда, используя рекуррентные формулы (40), можно найти остальные неизвестные 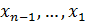в процессе обратной прогонки.

Число операций, которое требуется для решения системы общего вида (1) методом Гаусса, растет при увеличении числа неизвестных n пропорционально n ³. Метод прогонки сводится к двум циклам: сначала по формулам (41) рассчитываются прогоночные коэффициенты, затем с их помощью по рекуррентным формулам (40) находятся компоненты решения системы 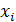. Это означает, что с увеличением размеров системы число арифметических операций будет расти пропорционально n, а не n ³. Таким образом, метод прогонки в пределах сферы своего применения является существенно более экономичным и довольно просто реализуется на компьютере в программном виде.

Во многих прикладных задачах, которые приводят к СЛАУ с трехдиагональной матрицей, ее коэффициенты удовлетворяют неравенствам

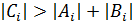. (44)

Если выполняются неравенства (44), то система (36) называется системой с диагональным преобладанием.

В случае если система (36) является системой с диагональным преобладанием то справедлива следующая лемма.

Лемма. Если для системы с трехдиагональной матрицей выполняется условие диагонального преобладания (44), то прогоночные коэффициенты удовлетворяют неравенствам

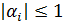. (45)

Неравенство (45) для прогоночных коэффициентов 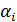делает метод прогонки устойчивым к ошибкам, которые неизбежны при компьютерных вычислениях в результате округления чисел.

Пример 1. Решить систему методом прогонки

,

,

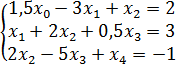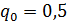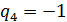
Дата добавления: 2014-12-27