Парабола и её уравнение

Параболой называется множество точек плоскости, равноудаленных от заданной точки (называется фокусом) и данной прямой (называется директрисой ).

Фокус параболы принято обозначать буквой F, директрису – буквой d, расстояние от фокуса до директрисы – буквой p (p>0). Рассмотрим основные случаи расположения параболы относительно осей координат.

Каноническое уравнение параболы, фокус которой расположен на оси абсцисс, имеет вид: y² = 2px или y² = -2px.

Эти два случая представлены в таблице 7.1.

Таблица 7.1.

Свойства и графики парабол вида y²=2px и y²= –2px

Чертеж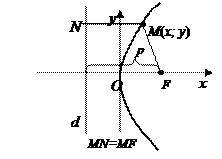
Положение фокуса   Координаты фокуса   Уравнение директрисы   Уравнение параболы	На положительной полуоси Ox y^2=2px	На положительной полуоси Ox 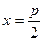y^2=–2px

Каноническое уравнение параболы, фокус который расположен на оси ординат, имеет вид: x² = 2py или x² = –2py.

Эти два случая представлены в таблице 7.2.

Таблица 7.2.

Свойства и графики парабол вида х²=2pу и х²= –2pу

M (x; y) Чертеж	МN=MF	МN=MF · M (x; y) y F x O d N p ·
Положение фокуса   Координаты фокуса   Уравнение директрисы   Уравнение параболы	На положительной полуоси Oy x^2=2pу	На положительной полуоси Oy x^2=–2pу

Пример 7.5. Найдите координаты фокуса и уравнение директрисы параболы, заданной уравнением y ²=8 x.

Решение. Из канонического уравнения параболы y²=2px следует, что 2 p =8, т.е. p =4, откуда p /2=2. Значит, точка F (2; 0) – фокус параболы, а x =2 – уравнение ее директрисы.

Контрольные вопросы:

1. Что называется кривой второго порядка?

2. Дайте определение окружности. Каким уравнением она задается?

3. Дайте определение эллипса. Каково каноническое уравнение эллипса?

4. Какая линия называется гиперболой? Каким каноническим уравнением она задается?

5. Что называют фокусом и директрисой параболы? Какие случаи расположения параболы в зависимости от ее канонического уравнения существуют?

РАЗДЕЛ 3. ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА

Математическим анализом называют систему дисциплин, объединенных следующими характерными чертами. Предметом их изучения являются количественные соотношения окружающего мира (в отличие от геометрических дисциплин, занимающихся его пространственными свойствами). Эти соотношения выражаются при помощи чисел, как и в алгебре. Но в алгебре рассматриваются преимущественно постоянные величины (преобразование выражений, уравнения - они характеризуют состояние), а в математическом анализе – переменные величины, характеризующие процессы. В основе изучения зависимости между переменными величинами лежит понятие функции.

Зачатки методов математического анализа можно встретить еще у древнегреческих математиков. Так, Архимед (287–212 гг. до н.э.) при вычислении площадей некоторых фигур и при определении объема шара по существу использовал интегральное исчисление, хотя, естественно, не знал его общих методов. Систематическое развитие эти методы получили в XVII веке. Одним из основателей математического анализа стал английский ученый Исаак Ньютон (1643–1727). Исследования в области механики привели его к проблемам дифференциального и интегрального исчисления. Одновременно с Ньютоном проблемами анализа занимался и немецкий математик Готфрид Вильгельм Лейбниц (1646–1716). Оба этих великих ученых не только завершили создание дифференциального и интегрального исчисления (получившего название анализа бесконечно малых величин), но и заложили основы учения о рядах и дифференциальных уравнениях.

Грандиозные успехи естествознания и математики в последующие три столетия во многом были предопределены великим открытиям Ньютона и Лейбница. В XVIII веке большой вклад в развитие математического анализа внес швейцарский математик Леонард Эйлер (1707–1783), свыше 30 лет проработавший в России. Систематизацией уже имеющихся результатов, а также дальнейшим развитием теории занимались многие французские математики: Жан Даламбер (1717–1783), Жозеф Лагранж (1736–1818), Пьер Лаплас (1749–1827), А.Лежандр (1752–1833), Ж.Фурье (1768–1830). К концу XVIII века был накоплен огромный фактический материал, но он был недостаточно разработан в логическом отношении. Многие понятия ученые воспринимали интуитивно.

Очевидные противоречия привели к критическому пересмотру в XIX веке существующих методов и четкому логическому построению математического анализа. Только в XIX веке были даны строгие определения функции, непрерывности, были уточнены понятия предельного перехода и основанные на нем понятия производной и интеграла. Современное понятие функции сформировалось в первой половине XIX века благодаря исследованиям таких выдающихся математиков, как Николай Иванович Лобачевский (1792-1856), Петер Дирихле (1805–1859) и др. Производная была определена как предел отношения приращения функции к приращению аргумента (французский математик Огюстен Коши (1780–1856)), интеграл – как предельное значение интегральных сумм (немецкий математик Бернхард Риман (1826–1866)). До сих пор математическое образование основывается на этих подходах, хотя в ХХ веке они получили значительное развитие. Тогда же вошли в употребление термины математика "элементарная" (математика, предшествовавшая рождению математического анализа) и "высшая" (начинается с понятий производной, предела и интеграла).

Одним из важнейших завоеваний математического анализа в XIX веке стало рождение теории аналитических функций и функций комплексного переменного. Следует упомянуть немецкого математика Карла Гаусса (1777–1855), ставшего основателем теории функций комплексного переменного и определившего понятие предела, русских математиков Пафнутия Львовича Чебышева (1821–1866), создателя конструктивной теории функций, Софью Васильевну Ковалевскую (1850–1891), немецкого математика Давида Гильберта (1862–1943). Важнейшие труды, касающиеся стройного логического построения математического анализа, принадлежат немецким математикам Карлу Вейерштрассу (1815–1897), ЮлиусуДедекинду (1831–1916) и Георгу Кантору (1845–1918).

В ХХ веке, уже на новом уровне, происходит всё большее слияние геометрии и математического анализа. Областью приложения анализа становятся кривые и поверхности, расположенные в многомерных пространствах с дополнительной алгебраической структурой. Исследования в области математического анализа продолжаются и в наши дни.

ГЛАВА 3.1. ТЕОРИЯ ПРЕДЕЛОВ

Понятие предела – одно из основных понятий математического анализа, на котором базируются многие важные определения, в частности, определение производной. Истоки понятия предела следует искать в Древней Греции. Некоторым подобием предельного перехода был метод исчерпывания, изобретенный Евдоксом (ок. 408–355 до н.э.). В работах Архимеда (ок. 287–212 до н.э.) и Евклида (конец IV-III век до н.э.) этот метод дал поразительные результаты. В новое время идеи предела появляются у немецкого астронома и математика Иоганна Кеплера (1571–1630), итальянского математика БонавентураКавальери (1598-1647), английского математика Джона Валлиса (1616-1703).

Слово "лимит" (предел) произошло от латинского limes (limite) – "межа", "граница". Этим словом впервые воспользовался Исаак Ньютон. Однако исторически сложилось так, что точное определение такого ключевого понятия, как предел, и такого важного понятия, как непрерывность, вплоть до конца XVIII века отсутствовали. Соответственно, и многие математические рассуждения содержали пробелы, а иногда были даже ошибочны. Характерный пример – определение непрерывности. Эйлер, Лагранж и даже Фурье (а он работал уже в начале XIX века) называли непрерывной функцию, заданную на области определения одним аналитическим выражением.

Тем самым бурно развивающаяся "новая" математика XVII-XVIII века не отвечала стандартам строгости, привычным для ученых еще со времен древних греков. Интуиция, столь необходимая математикам, существенно опередила логику. Гениальная интуиция таких гигантов, как Ньютон, Лейбниц, Эйлер, помогала им избегать ошибок. Но необходимы были прочные логические основы.

Решительный шаг к созданию прочного фундамента анализа был сделан в 20-е годы XIX века французским математиком Огюстеном Коши (1789–1857), предложившим точное определение пределов функции и последовательности и на их основе доказавшим многие фундаментальные теоремы анализа, в частности теоремы о пределах. Несколько раньше (в 1821 году) определение предела, непрерывности и ряд других замечательных результатов получил чешский математик Бернард Больцано (1781-1848), но его работы стали известны много позднее. После лекций известного немецкого профессора Карла Вейерштрасса (1815-1897), которому принадлежит современное обозначение предела, определение предела по-Коши (на языке ε-δ) прочно вошло в обиход и используется нами по сей день.

Дата добавления: 2014-12-27