
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
|
|
|
|
| Дифференциальное уравнение | 
| ||
| Характеристическое уравнение | 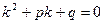
| ||
| Дискриминант | D>0 | D=0 | D<0 |
| Корни характеристического уравнения | 
| 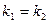 = k = k
| 
|
| Общее решение дифференциального уравнения | 
| 
| 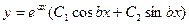
|
Рассмотрим решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами на конкретных примерах.
Пример 41.3. Решите дифференциальное уравнение: 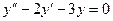 .
.
Решение. Составим характеристическое уравнение 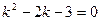 . Найдем его корни.
. Найдем его корни. 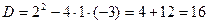 ;
; 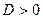
 существуют два различных корня k 1 и k 2.
существуют два различных корня k 1 и k 2.
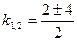 ;
; 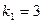 или
или  .
.
Тогда, пользуясь таблицей 41.1, находим общее решение дифференциального уравнения по формуле  :
: 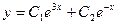 .
.
Ответ: 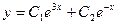 .
.
Пример 41.4. Решите дифференциальное уравнение:  .
.
Решение. Составим характеристическое уравнение 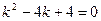 . Найдем его корни.
. Найдем его корни.  ;
; 
 существуют два равных корня k 1 = k 2 = k.
существуют два равных корня k 1 = k 2 = k.
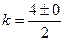 ;
;  .
.
Тогда, пользуясь таблицей 41.1, находим общее решение дифференциального уравнения по формуле  :
: 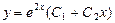 .
.
Ответ: 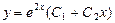 .
.
Пример 41.5. Решите дифференциальное уравнение: 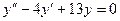 .
.
Решение. Составим характеристическое уравнение  . Найдем его корни.
. Найдем его корни. 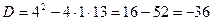 ;
; 
 существуют два комплексных корня k 1 и k 2.
существуют два комплексных корня k 1 и k 2.
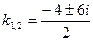 ;
; 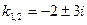

 ,
,  .
.
Тогда, пользуясь таблицей 41.1, находим общее решение дифференциального уравнения по формуле 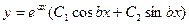 :
: 
Ответ:  .
.
Контрольные вопросы:
- Какой вид имеет простейшее дифференциальное уравнение второго порядка? Как оно решается?
- Сколько произвольных постоянных содержит общее решение дифференциального уравнения второго порядка?
- Как определяется в общем виде линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами?
- Что такое характеристическое уравнение?
- Какой вид имеет общее решение дифференциального уравнения второго порядка с постоянными коэффициентами, если корни характеристического уравнения: а) действительные и различные (
 ); б) действительные и равные (
); б) действительные и равные (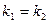 = k); в) комплексные сопряженные (
= k); в) комплексные сопряженные ( )?
)?
РАЗДЕЛ 4. ОСНОВЫ ТЕОРИИ КОМПЛЕКСНЫХ ЧИСЕЛ
|
|
|
Введение комплексных чисел было связано с открытием решения кубического уравнения. В середине ХVI века итальянские математики Никколо Тарталья (1499-1557) и Джероламо Кардано (1501-1576) представили миру способ решения уравнения третьей степени. Но один из возможных случаев так и остался для них загадкой. Оказалось, что при выполнении вспомогательных действий рассматриваемая система не имела решений, а исходное уравнение имело действительный корень. На это загадочное явление впервые пролил свет другой итальянский математик Рафаэле Бомбелли (1526-1572).
Бомбелли первым ввел в алгебру мнимые величины. Квадратный корень из отрицательного числа, как заметил Бомбелли, не может быть ни положительным, ни отрицательным числом. Он предложил назвать эти новые "софистические" числа "плюсом из минуса"  , когда их нужно складывать, и "минусом из минуса"
, когда их нужно складывать, и "минусом из минуса" 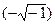 , когда их нужно вычитать. И тогда у любого кубического уравнения прекрасно отыскивались корни! С этого момента комплексные числа уже нельзя было игнорировать. Бомбелли в своей "Алгебре" (1560, издана 1572) дал первое формальное обоснование действию над комплексными числами. Определение мнимой единицы, данное Бомбелли, за прошедшие 400 лет по свой сути не изменилось, а арифметические действия с ней производятся именно так, как это делала Бомбелли в ХVI веке.
, когда их нужно вычитать. И тогда у любого кубического уравнения прекрасно отыскивались корни! С этого момента комплексные числа уже нельзя было игнорировать. Бомбелли в своей "Алгебре" (1560, издана 1572) дал первое формальное обоснование действию над комплексными числами. Определение мнимой единицы, данное Бомбелли, за прошедшие 400 лет по свой сути не изменилось, а арифметические действия с ней производятся именно так, как это делала Бомбелли в ХVI веке.
Мнимые числа, введенные Бомбелли, более двух столетий воспринимались лишь как удобные символы. Математики применяли их только в промежуточных выкладках, но для результата использовали лишь "настоящие" – действительные числа. Лейбниц в 1702 году писал: "Мнимые числа – это прекрасное и чудесное убежище божественного духа, почти что сочетание бытия с небытием". Исчерпывающие правила действий с комплексными числами дал в середине ХVIII века русский математик Леонард Эйлер (1707-1783) – один из величайших математиков всех времен и народов. Именно он предложил современное обозначение мнимой единицы – i.
|
|
|
Комплексные числа не были в достаточной мере востребованы математиками еще и потому, что очень трудно было их представить. Наглядно представить мнимые числа попытался еще в ХVII веке английский ученый Джон Валлис (1616-1703), но эти попытки были не слишком удачные. В 1799 году датский математик - землемер Каспар Вессель (1745-1818) предложил простую геометрическую интерпретацию комплексных чисел, однако его работа осталась незамеченной, поскольку Вессель не имел контактов с научными кругами своего времени. Лишь через три десятка лет немецкий математик Карл Фридрих Гаусс (1777-1855) выпустил в свет свой труд "Теория биквадратных вычетов", в котором дал такое же геометрическое представление комплексных чисел, как и Вессель. Именно после опубликования этой работы в 1831 году геометрическое изображение комплексных чисел получило широкую известность и признание. Идея Веселя и Гаусса настолько прозрачна, что остается только удивляться, почему никто из ученых не додумался до нее раньше.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 974; Нарушение авторских прав?; Мы поможем в написании вашей работы!