Математична модель

Постановка задачі та побудова моделі

Попередні зауваження

Розглянута вище одновидова популяція є надзвичайно спрощеною й ідеалізованою екологічною системою. Насправді ж популяції в природі існують, а точніше, співіснують у вигляді співтовариств різних видів, які знаходяться в різноманітних стосунках. Тому цілком природним і логічним є дослідження наступних за складністю моделей співіснування двох популяцій. Класифікація таких моделей здійснюється у відповідності з типом міжвидових стосунків:

а) модель «хижак-жертва»;

б) модель «паразит-хазяїн»;

в) модель конкуренції за обмежені ресурси існування тощо.

Вище зазначалося, що сучасна математична екологія як наука почала формуватися в 20-30-х роках XX ст. Визначальною подією для її розвитку стала поява у 1931 р. книги відомого італійського
математика, засновника сучасної математичної екології Віто Воль­тéрри, «Математична теорія боротьби за існування». У цій книзі вперше систематично розглянуто математичні моделі, що описують відносини між двома біологічними видами. Один з розділів книги присвячений аналізу взаємин між хижаками й жертвами. Ці драматичні стосунки ми покладемо в основу майбутньої навчальної роботи.

Метою дослідження поставимо питання про характер зміни чисельності представників кожного виду з плином часу.

Нехай у знайомому нам ставку з карасями (жертвами) з’явля­ються щуки (хижаки).

Припущення 1. За умови, що хижаки й жертви ізольовані одні від інших, а обмеження на ресурси середовища для жертв (карасів) відсутні, динаміку кожної популяції для достатньо малих проміжків
часу Δ t можна описати законом Мальтуса, де всі індекси «1» відносяться до жертв, а індекси «2» – до хижаків.

Тут 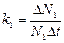і – відносні прирости чисельності жертв і хижаків за одиницю часу. Знак «-» у другому рівнянні означає, що ізольовані від жертв (їжі) хижаки матимуть негативний приріст, тобто їхня кількість із часом буде зменшуватись, і вони будуть гинути. Але коли хижаки й жертви опиняються поруч, зміни чисельності популяцій стають взаємозалежними. За цих умов приймемо

Припущення 2. Швидкість приросту жертв повинна залежати від розмірів популяції хижаків, причому вона буде зменшуватися зі зростанням чисельності хижаків. Для швидкості приросту хижаків
повинно виконуватись протилежне: швидкість приросту хижаків
буде збільшуватись одночасно з ростом чисельності жертв. Оскільки хижак з’їдає жертву при зустрічі з нею, приймемо

Припущення 3. Число зустрічей пропорційне як кількості жертв N ₁, так і хижаків N ₂, тобто твором N ₁× N ₂.

Для опису динаміки популяцій В. Вольтéрра запропонував таку систему рівнянь:

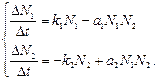(1)

Тут N ₁, N ₂ – чисельність жертв і хижаків в деякий момент часу;

k ₁, a ₁, k ₂, а ₂ – постійні коефіцієнти.

Завдання. Поясніть, чому вирази, пропорційні добутку N ₁× N ₂, входять до рівнянь системи (1) з протилежними знаками?

Перепишемо систему (1) у формі кінцевих різниць:

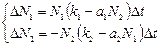(2)

Система рівнянь (1) або (2) є математичною моделлю динаміки співіснування двох біологічних видів на основі відносин «хижак – жертва». У математичної екології ця модель відома під назвою «модель Вольтéрри – Лотки».

В. Вольтéрра згадував, що у 1925 році його приятель-біолог розповів цікавий факт: коли в роки першої світової війни й у перші
повоєнні роки інтенсивність промислів на Адріатиці різко скоротилася, то в уловах почали спостерігати помітне зростання відносної частки хижих риб. Щоб пояснити це, Вольтéрра і запропонував модель (1).

Приймемо далі

Припущення 4. Коефіцієнти моделі k ₁, а ₁, k ₂, а ₂ не залежать від того, яку саме частину кожної популяції ми бажаємо описати. Таку популяцію називають просторово однорідною.

У разі неоднорідного розподілу хижаків і жертв може виникнути ситуація, коли частина хижаків буде знаходитися дуже далеко від жертв (а ₂ малий), а решта – поблизу (а ₂ великий). У такому разі опис кожної популяції системою рівнянь (1) стає неможливим. Тому
будемо вважати, що коефіцієнти моделі є постійними в просторі і не змінюються з плином часу.

Однак з’ясувалося, що модель Вольтéрри – Лотки не має точних аналітичних розв’язків, тобто подати N ₁(t) і N ₂(t) через відомі елементарні функції неможливо. Тому єдине, що залишається в такій ситуації – це скористатись чисельним методом. Для нас цей факт є визначальним: адже в попередніх задачах (моделях) аналітичні розв’язки існували, однак ми наполегливо опановували чисельний метод.
Виявляється, не дарма.

Дата добавления: 2015-01-03