Постановка задачі. Параболічна й гіперболічна орбіти

Параболічна й гіперболічна орбіти

Надаючи, нарешті, початковій швидкості значення v_y (0) = v _{1 К} , тобто вводячи до Н8 новий множник, отримуємо параболічну (розім­кнену) траєкторію (рис. 8.4).

Рис. 8.4.

Завдання

1. Спочатку з’ясуєте, за якої умови траєкторія супутника стає
гіперболічною, а потім перевірте цю умову на моделі.

2. Закон тяжіння не відрізняє штучний супутник від природного. Планети Сонячної системи є природними супутниками Сонця, і при цьому добре виконується умова т_пл << M_С, оскільки маса Сонця приблизно в 900 разів більша за масу всієї іншої речовини Сонячної системи (усіх планет з їх атмосферами, астероїдів, комет, метеорної
речовини тощо). Враховуючи цей факт, змоделюйте рух Землі навколо Сонця, змінивши потрібним чином у вже побудованій моделі вміст деяких комірок стовпця H.

Висновки

1. Залежно від початкових умів траєкторією руху тіла, на яке діє сила всесвітнього тяжіння, може бути одна з кривих другого
порядку – коло, еліпс, парабола чи гіпербола.

2. Усі розглянуті моделі можна об’єднати в одну групу за спільною ознакою m_супутн<< M_{центр тіла}. Усвідомлення цього факту стає умовою переходу до наступного етапу роботи.

8.2. Рух природного супутника планети
або компонентів системи «подвійна зірка»

Природні супутники планет мають маси, якими не завжди можна нехтувати в порівнянні з масами самих планет, тому моделювання руху компонентів таких систем («планета – природний супутник») є більше трудомістким завданням. Знову розпочнемо аналіз із найбільш простого випадку – руху уздовж колових орбіт (рис. 8.5).

1. Обидва ці тіла – центральне масою m ₁ і супутник масою m ₂ – обертаються навколо нерухомої точки С – їх загального центру мас. При цьому вони увесь час знаходяться на одній прямій, яка сполучає тіла і проходить через точку С. Ця точка (центр мас) ділить відстань R між тілами на відрізки r ₁ і r ₂ у відношенні

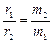. (4)

З (4) випливає 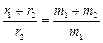або ,

Рис. 8.5.

звідки

.

Переходячи до проекцій, отримуємо для моменту часу t = 0:

, (5)

де х ₁, х ₂– координати тіл у системі відліку, пов’язаній зі спільним центром мас – точкою С.

2. Певних уточнень потребують вирази для прискорень.

Сила тяжіння надає прискорень обом тілам:

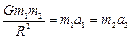, звідки .

Для моменту часу t = 0 у відповідності з рис. 8.5 отримуємо:

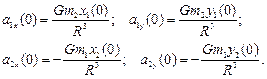(6)

Із задачі про штучний супутник нам відомо, що вигляд траєкторії рухомого тіла визначається початковими умовами, і зокрема,
початковими швидкостями v _{1 y} (0) і v _{2 y} (0).

За аналогією зі згаданою задачею прискорення, що їх надає сила всесвітнього тяжіння, є нормальними (доцентровими) і спрямованими до спільного центру мас. Зокрема, для а _{2 x} (0) із (6) маємо .

Це прискорення забезпечує стійке обертання тіла m ₂ навколо
загального центру мас з лінійною швидкістю v _{2 y} (0). Таким чином,

а _{2 x} (0) = 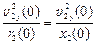у відповідності з добре відомою формулою 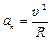. Отже, а _{2 x} (0) = 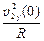, або , звідки 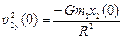і, нарешті,

(7)

Виразимо v _{1 y} (0) через v _{2 y} (0) за допомогою наступних міркувань.

Знаходячись увесь час на одній прямій, обидва тіла мають однакові періоди обертання Т ₁ = Т ₂: , звідки

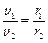, (8)

що для t = 0 у проекціях дає

. (9)

З (8) і (9) маємо .

І остаточно отримуємо:

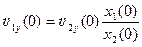. (10)

Завдання. Покажіть, що для довільного моменту часу вираз (6) набуває вигляду:

(7)

де (x ₁, y ₁), (x ₂, y ₂) – відповідно координати першого і другого тіл у довільний момент часу, а – відстань між тілами.

Дата добавления: 2015-01-03