Інтерполювання у випадку рівновіддаленихвузлів: перша інтеполяційна формула Ньютона

Пусть для функции 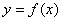заданы значени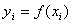я для

равноотстоящих значений независимой переменной ,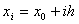

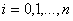, где 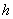- шаг интерполяции. Требуется подобрать полином 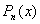степени не выше n, принимающий в точках 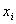значения .

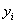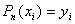. (4.13)

Условия (4.13) эквивалентны тому, что

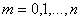, . (4.14)

Следуя Ньютону, будем искать многочлен в виде

.(4.15)

Используя обобщённую степень выражение (4.15) запишем так:

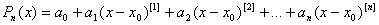. (4.16)

Задача состоит в определении коэффициентов 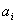, 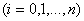многочлена 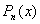. Полагая в выражении (4.16) 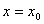получаем: . Чтобы найти коэффициент 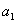, составим первую конечную разность

.

Полагая в последнем выражении 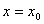, получаем: 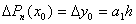, откуда находим 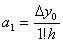. Для определения 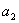найдём конечную разность второго порядка

.

Полагая в последнем выражении 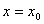, получаем: 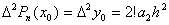, откуда 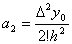. Последовательно продолжая этот процесс, мы обнаружим, что 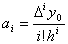, , 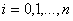, 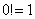. Подставляя найденные значения коэффициентов 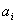в (4.16), получим интерполяционный полином Ньютона

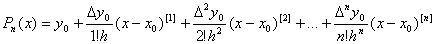. (4.17)

Для практического использования интерполяционную формулу Ньютона (4.17) обычно записывают в преобразованном виде. Для этого введём новую переменную 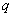по формуле: .

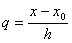Тогда .

Подставляя эти выражения в (4.17), получаем, что первая интерполяционная формула Ньютона имеет вид:

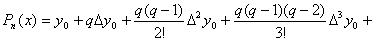
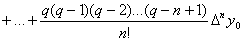, (4.18)

где 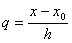. Величина 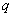представляет собой число шагов, необходимых для достижения точки 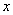, исходя из точки 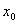. Полученную формулу ещё называют формулой Грегори - Ньютона, т.к. она впервые была получена Джемсом Грегори в 1670 г., а затем, начиная с 1676 г., рассматривалась в ряде работ Исаака Ньютона, посвященных вопросам интерполирования.

Эта формула используется для интерполирования функции в окрестности начального значения 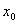, где 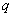мало по абсолютной величине. Если в формуле (4.18) положить n=1, то получим формулу линейной интерполяции:

.

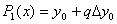При n=2 будем иметь формулу параболического или квадратичного интерполирования

.

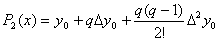Если таблица значений функции конечна, то n ограничено, а именно n не может быть больше числа значений функции уменьшенного на единицу. Если дана неограниченная таблица значений функции y, то число n может быть любым. Практически в этом случае число n выбирается так, чтобы разность 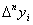была постоянной с заданной степенью точности.

Погрешность первой интерполяционной формулы Ньютона имеет вид:

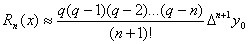. (4.19)

Дата добавления: 2015-01-03