Побудова інтерполяційної функції. Системи Чебишова. Основні напрямки використання теорії інтерполяції

Общая задача интерполирования заключается в построении функции, вообще говоря, отличной от данной y = f(x), которая может быть известна, но задана слишком сложным аналитическим выражением, или неизвестна и задана в виде таблицы значений. Построенная функция должна принимать в заданных точках те же значения, что и данная функция f(x). В этом определении сформулированы две задачи:

1. Построение для функции, имеющей аналитическое выражение, такой более простой функции, которая заменила бы данную в вычислениях.

2. Для функции, заданной таблицей, найти такую формулу, которая давала бы возможность находить значения функции для промежуточных значений аргумента.

Пусть на отрезке [a,b] заданы n+1 точек x0 x1..., x n. Эти точки называются узлами интерполяции. И даны значения некоторой функции f(x) в этих точках

f(xi) = yi.

Требуется построить функцию φ(x) (интерполирующая функция), принадлежащую известному классу и принимающую в узлах интерполяции те же значения, что и f(x), т.е.

φ(xi) = yi.

Геометрически это означает, что нужно найти кривую y = φ(x), некоторого определённого типа, проходящую через заданную систему точек Mi (xi, yi), i=0,1,...,n.

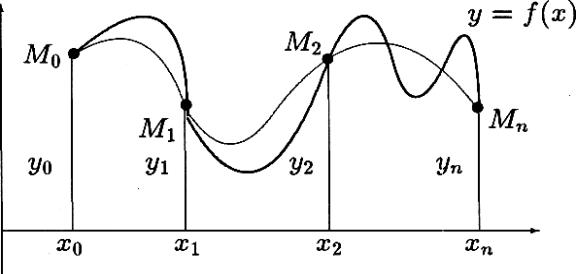
В такой общей постановке задача может иметь бесчисленное множество решений. Однако эта задача становится

однозначной, если в качестве приближающей функции искать многочлен степени не выше n, удовлетворяющий условиям (4.2). Полученную интерполяционную формулу y = φ(x) обычно используют для приближенного вычисления значений данной функции f(x). При этом различают интерполирование в узком смысле, когда x Є [x0, xn], и экстраполирование, когда x<x0 или x>xn. В дальнейшем под термином "интерполирование" мы будем понимать как первую, так и вторую операции.

Системи Чебишова.

Рассмотрим квадратурную формулу

,

где - постоянные коэффициенты. Чебышев предложил выбирать абсциссы таким образом, чтобы:

1) коэффициенты были равны между собой;

2) квадратурная формула являлась точной для всех полиномов до степени "n" включительно.

Покажем, как могут быть найдены в этом случае величины и 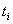. Полагая взяв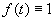

.

.

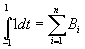Следовательно, квадратурная формула Чебышева имеет вид:

.

Для определения 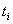используем то, что формула (6.16) должна быть точной для функций вида:

.

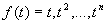Подставляя эти функции в формулу получим систему уравнений

Из системы могут быть определены неизвестные

. Чебышев показал, что решение системы сводится к нахождению корней некоторого алгебраического уравнения степени " ". Узлы 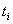являются действительными при =1,2,…,7,9. При =8 и 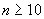среди узлов всегда имеются комплексные. В этом состоит принципиальный недостаток квадратурной формулы Чебышева. Свою формулу Чебышев П.Л. вывел в 1873 году.

Дата добавления: 2015-01-03