Метод Адамса для наближеного розв’язання звичайних диференціальних рівнянь

Метод Рунге-Кута для наближеного розв’язання звичайних диференціальних рівнянь

Для того чтобы увеличить точность результата по сравнению с методом Эйлера, в методе Рунге - Кутта при разложении функции в ряд Тейлора сохраняют четыре члена разложения.

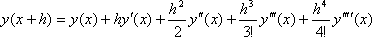
Производные 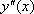, , 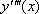могут быть найдены последовательным дифференцированием уравнения. В результате получаются следующие формулы для вычислений:

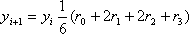, (11.15)

где , , ,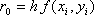

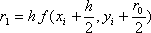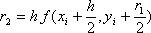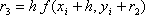
Метод Рунге - Кутта является методом повышенной точности, погрешность на каждом шаге порядка 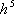. Так, например, при 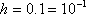метод Эйлера дает только два верных знака, а метод Рунге - Кутта дает пять верных знаков. С алгоритмической точки зрения метод Рунге - Кутта не имеет принципиальных отличий от метода Эйлера.

Метод Адамса — разностный метод численного интегрирования обыкновенных дифференциальных уравнений, позволяющий вычислять таблицу приближённых значений решения в начальных точках. Назван по имени предложившего его английского астронома Дж. К. Адамса в 1855. Пусть требуется найти приближенное решение дифференциального уравнения y'=f(x,y), удовлетворяющее начальному условию y(x0) = y0. Численное решение задачи состоит в построении приближенного значения y1 решения уравнения y(x) в точке x1 = x0 + h. Методами Адамса называют группу многошаговых методов, в которых приближенное решение yn+1=y(xn+1) в точке xn+1=x0+h(n+1) вычисляется по формуле, использующей полином P(x) наименьшей степени, интерполирующий правую часть f(x,y) по значениям fn, fn-1,...,fn-k+1, fr = f(xr,yr). Методы, в которых P(x) = Pkn(x) называют k-шаговыми явными методами Адамса-Башфорта, а методы, в которых P(x) = Pk+1n+1 - (k+1)-шаговыми неявными методами Адамса-Мултона. Методы Адамса k-го порядка требуют предварительного вычисления решения в k начальных точках. Часто для вычисления дополнительных начальных значений используется метод Рунге-Кутты 4-стадийный 4-го порядка точности. Локальная погрешность методов Адамса k-го порядка O(hk). Методы Адамса обладают лучшей, по сравнению с методами Рунге-Кутты устойчивостью.

Все к тому же методу Адамса:

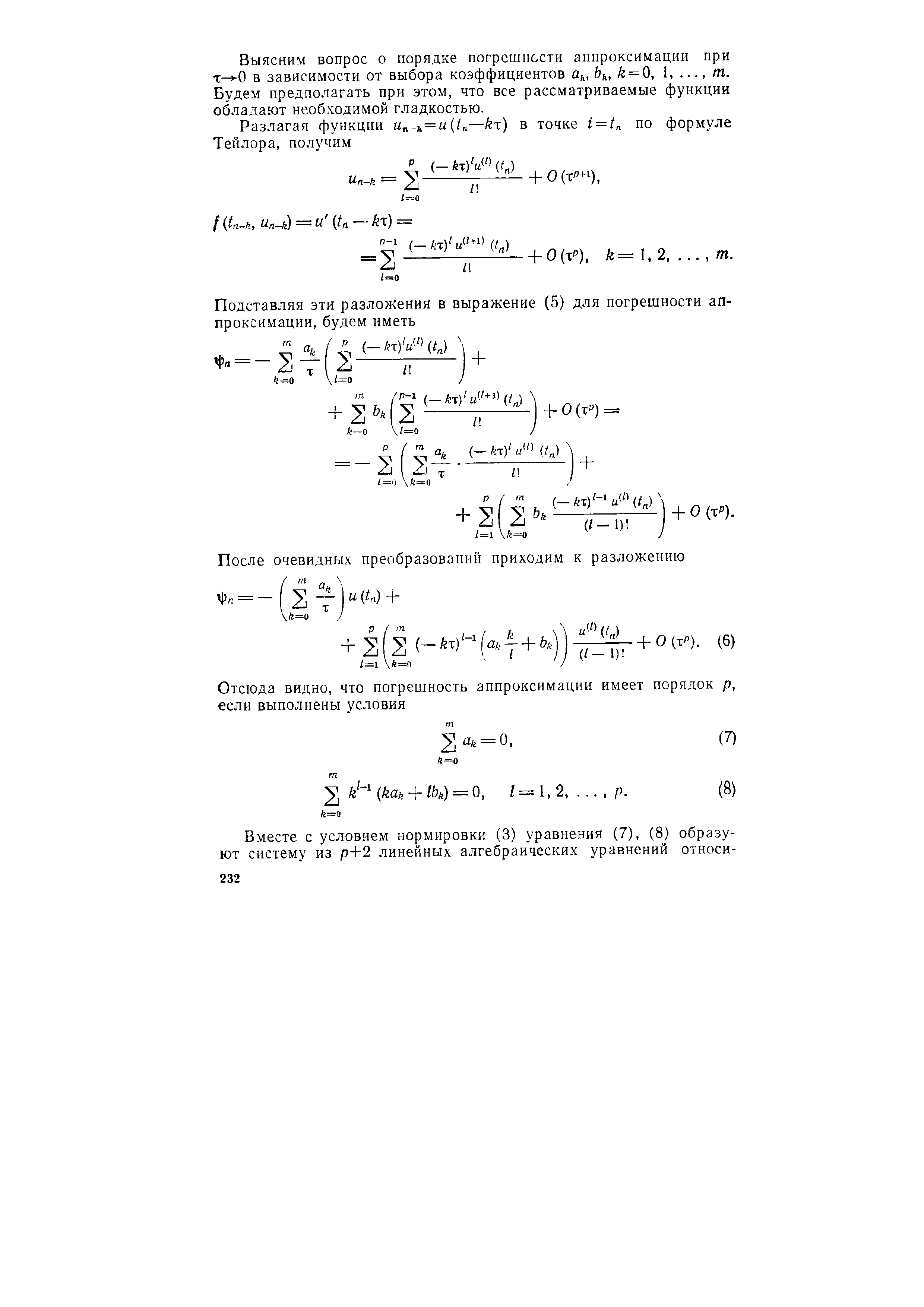
Дата добавления: 2015-01-03