Доказательство. Если бы все элементы были различны, то число перестановок равнялось бы n

Если бы все элементы были различны, то число перестановок равнялось бы n!. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. Возьмем, например, перестановку

aa... a bb... b... xx... x,

n1 n2 n_k

в которой сначала выписаны элементы первого типа, потом все элементы второго типа, …, наконец, все элементы k-го типа. Элементы первого типа можно переставлять n₁! способами, это ничего не меняет. Точно так же ничего не меняют n₂! перестановок элементов второго типа,..., n_k! перестановок элементов k-го типа. Перестановки элементов первого типа, второго типа и т. д. можно делать независимо друг от друга. По правилу произведения элементы перестановки можно переставлять n₁!∙n₂! ∙...∙n_k! способами так, что она останется неизменной. То же самое верно и для любого другого расположения элементов. Поэтому множество всех n! перестановок распадается на части, состоящие из n₁! ∙n₂! ∙...∙n_k! одинаковых перестановок каждая. Значит, число различных перестановок с повторениями, которые можно сделать из данных элементов, равно

P(n₁,n₂,…,n_k)= .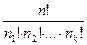

Задача.

Сколькими способами можно поставить в ряд 3 красных, 4 синих и 5 зеленых кубиков?

Решение.

По формуле перестановок с повторениями получаем: Р(3, 4, 5)= .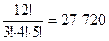

Задача.

Слово – любая конечная последовательность букв русского алфавита. Сколько различных слов можно составить из слова КАСАТЕЛЬНАЯ, если необходимо использовать все буквы?

Решение.

В слове имеется 3 буквы А и еще 8 различных букв. По формуле перестановок с повторениями получаем: Р(1, 1, 1, 1, 1, 1, 1, 1, 3)= =6 652 800.

Сочетания

До сих пор при составлении комбинаций из элементов различных типов нас интересовал порядок расположения элементов. Но некоторый класс задач приводит к составлению комбинаций, в которых порядок элементов совершенно не важен.

Задача 1.

Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал 5 различных цветов?

Решение.

Это задача на размещения без повторений Ответ: =5×4×3=60 способов составить флаг.

Задача 2.

Сколькими способами можно выбрать три краски из имеющихся пяти?

Решение.

В данном случае порядок выбора красок не важен. Поэтому количество способов выбора красок, полученное в предыдущей задаче, необходимо разделить на 3! – количество способов переставить выбранные краски. Ответ: 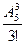=10.

Эта задача относится к классу задач о сочетаниях.

Сочетаниями из n элементов по k называют всевозможные комбинации по k элементов, составленные из данных n элементов. Комбинации отличаются друг от друга составом, но не порядком элементов.

Количество сочетаний из n элементов по k обозначают .

Формула для вычисления числа сочетаний получается из формулы для вычисления количества размещений. Составим сначала все k-сочетания из n элементов, а потом переставим входящие в каждое сочетание элементы всеми возможными способами. При этом получатся все k-размещения из n элементов, причем каждое только по одному разу. Элементы каждого k-сочетания можно переставить k! способами, а число этих сочетаний равно . Значит, справедлива формула . Получаем .

Задача.

Два филателиста хотят обменяться марками. У одного для обмена есть 7 марок, у другого – 5. Сколькими способами они могут поменять две марки одного на две марки другого?

Решение.

Первый филателист должен выбрать 2 марки из 7. Он может это сделать способами. Второй должен выбрать 2 марки из 5. Он может это сделать 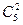способами. По правилу произведения получаем, × 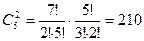способов совершить обмен.

Задача.

Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди них окажется ровно три туза?

Решение.

Необходимо выбрать трех тузов и семь «не тузов». Всего в колоде 4 туза. Поэтому выбрать из них 3 можно способами. «Не тузов» в колоде 48. Выбрать из них 7 можно способами. По правилу произведения получаем: × = 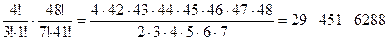способов выбрать из колоды 10 карт так, что среди них будет ровно три туза.

Свойства чисел

Числа обладают рядом замечательных свойств. Эти свойства можно доказывать по-разному. Можно прямо воспользоваться формулой 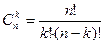. Однако часто удается получить доказательство из комбинаторных соображений.

1 свойство: P(k, n-k) =

Доказательство.

Комбинаторное доказательство.

Поставим по порядку все n элементов, из которых составляют сочетания, и зашифруем каждое сочетание комбинацией из n нулей и единиц. Каждому k-сочетанию соответствует комбинация из к единиц и n – k нулей, и наоборот. Отсюда и следует, что число сочетаний из n элементов по k совпадает с числом перестановок с повторениями из к элементов одного вида (единиц) и n – k элементов другого (нулей).

2 свойство – свойство симметричности

Доказательство.

.

Комбинаторное доказательство

Если выбрать из n различных предметов некоторое k-сочетание, то останется дополнительное (n – k)-сочетание, а дополнительным к (n – k)-сочетанию является исходное k-сочетание. Таким образом, k-сочетание и (n – k) сочетание образуют взаимно дополнительные пары, поэтому число этих сочетаний одно и то же.

3 свойство – основное свойство

Доказательство.

Комбинаторное доказательство.

Составим k-сочетание из n элементов а₁, а₂, …,a_n и разобьем их на два класса. В первый из них войдут сочетания, содержащие элемент a_n, во второй – не содержащие этого элемента. Если из любого сочетания первого класса откинуть элемент а_n, то останется (к –1)-сочетание, составленное из элементов а₁, а₂, …, a_n-1. Число таких сочетаний равно 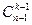. Поэтому в первый класс входит 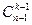комбинаций. Сочетания второго класса являются k-сочетаниями, составленными из элементов а₁, а₂, …,a_n-1. Поэтому их число равно . Поскольку любое k-сочетание принадлежит одному и только одному из этих классов, а общее число этих сочетаний равно , то, используя правило сложения, приходим к искомому равенству.

4 свойство:

Комбинаторное доказательство.

2ⁿ – число всех размещений с повторениями из элементов двух типов. Разобьем эти размещения на классы, отнеся в k-ый класс те, в которые входят k элементов первого типа и n–k элементов второго типа. Размещения k-го типа - это ни что иное, как всевозможные перестановки из k элементов первого типа и n–k элементов второго типа. Число таких перестановок равно P(k, n–k)=C(n, k). По правилу суммы общее число размещений всех классов равно . С другой стороны, это же число равно 2ⁿ.

5 свойство: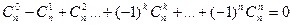

Комбинаторное доказательство.

Выпишем все сочетания из n элементов а₁, …,а_n и сделаем следующее преобразование: к сочетанию, не содержащему элемент а₁, допишем его, а из сочетаний, куда оно входит, вычеркнем. Легко проверить, что при этом снова получаются все сочетания, и притом по одному разу. Но при этом преобразовании все сочетания, имевшие четное число элементов, превратятся в сочетания, имеющие нечетное число элементов, и обратно. Значит сочетаний с четным и нечетным количеством элементов одинаковое количество (пустое сочетание тоже входит в рассмотрение). Это и выражает данная формула.

Задача.

На окружности отмечено 11 точек. Сколько существует многоугольников с вершинами в отмеченных точках?

Решение.

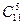Первый способ. Существует треугольников с вершинами в отмеченных точках, – четырехугольников, – пятиугольников, …, 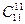– одиннадцатиугольников. Таким образом, по правилу суммы всего многоугольников + + +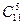…+ 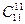. Из четвертого свойства следует, что это выражение равно 2¹¹- 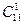- =1 982.

Второй способ. Любая из одиннадцати точек либо является вершиной рассматриваемого многоугольника, либо не является. Всего вариантов 2¹¹. Но одна или две точки не могут составлять многоугольник. Остается 2¹¹- 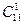- вариантов многоугольников с вершинами в отмеченных точках.

Сочетания с повторениями.

Задача.

В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Эта задача не является задачей на размещения с повторениями, так как порядок, в котором укладывают пирожные в коробку, несуществен. Поэтому она ближе к задачам на сочетания. Но от задач на сочетания она отличается тем, что в комбинации могут быть повторяющиеся элементы. Такие задачи называют задачами на сочетания с повторениями.

Чтобы решить задачу, поступим следующим образом. Зашифруем каждую покупку с помощью нулей и единиц. Сначала напишем столько единиц, сколько куплено наполеонов. Потом, чтобы отделить наполеоны от эклеров, напишем нуль, затем – столько единиц, сколько куплено эклеров, и т. д. Например, если куплено 3 наполеона, 1 эклер, 2 песочных и 1 слоеное пирожное, то получим такую запись: 1110101101. Ясно, что разным покупкам соответствуют разные комбинации из 7 единиц и 3 нулей. Обратно, каждой комбинации 7 единиц и 3 нулей соответствует какая-то покупка.

Таким образом, число различных покупок равно числу перестановок с повторениями, которые можно составить из 7 единиц и 3 нулей. А это число равно P(7,3)=120.

К тому же самому результату можно было прийти и другим путем, а именно: расположим в каждой покупке пирожные в таком порядке: наполеоны, эклеры, песочные и слоеные, а потом перенумеруем их. Но при нумерации будем к номерам эклеров прибавлять 1, к номерам песочных – 2, к номерам слоеных – 3. К номерам наполеонов ничего прибавлять не будем. Например, пусть куплено 2 наполеона, 3 эклера, 1 песочное пирожное и 1 слоеное. Тогда эти пирожные нумеруются так: 1, 2, 4, 5, 6, 8, 10. Ясно, что самый большой номер может быть 10, самый маленький – 1, а кроме того, ни один из номеров не повторяется, причем они образуют возрастающую последовательность. Обратно, каждой возрастающей последовательности из 7 чисел соответствует некоторая покупка. Например, последовательность 2, 3, 4, 5, 7, 8, 9 соответствует покупке из 4 эклеров и 3 песочных пирожных. Чтобы убедиться в этом, надо отнять от заданных номеров числа 1, 2, 3, 4, 5, 6, 7. Мы получим числа 1, 1, 1, 1, 2, 2, 2. Но 1 мы прибавляли к номерам эклеров, а 2 – к номерам песочных.

Отсюда, общее число покупок равно числу возрастающих последовательностей из 7 чисел от 1 до 10. А число таких последовательностей равно C(10,7)=120.

Сочетаниями с повторениями из n элементов по k называют всевозможные комбинации, составленные из элементов n видов по k элементов в каждой. Комбинации считаются различными, если они отличаются составом, но не порядком входящих в них элементов. В комбинацию могут входить элементы одного вида.

Количество сочетаний с повторениямиизn элементов по k обозначают . Общее правило вычисления количества сочетаний с повторениями:

Дата добавления: 2015-01-03