Решение задач 34—39 из учебника

Задача 34. Первая после листа определений задача, как обычно, предлагается детям для того, чтобы они освоились с новыми понятиями, в данном случае с правилами игры «сим». На начальном этапе ребятам наверняка потребуется некоторый контроль. Например, после того как учащиеся поработают с листом определений, стоит провести несколько партий игры «сим» на доске под контролем всего класса. При проведении кругового турнира в группах можно для каждой партии назначить одного-двух контролёров. Несмотря на то что при проведении двух партий одновременно турнир можно закончить гораздо быстрее, всё-таки лучше, чтобы процесс игры многократно проверялся (не только игроками, но и контролёрами). Чтобы контролёрам в группах было проще проверять, является ли данная позиция заключительной, можно перед началом турниров вместе обсудить, сколько всего должно быть проведено отрезков в случае ничьей (на окружности с пятью точками) и начиная с какого хода могут появиться одноцветные треугольники. Конечно, на листе определений ребята уже прочитали, что в случае ничьей на окружности с пятью точками игроки делают по пять ходов (проводят всего 10 отрезков), однако учащимся полезно убедиться в этом.

Надеемся, что заполнить турнирную таблицу ребятам будет нетрудно: подобные задания они уже выполняли для других игр.

Задача 35. В отличие от предыдущей задачи каждый учащийся здесь играет и за Первого, и за Второго и сам же является контролёром. С одной стороны, это проще, ведь можно подыгрывать. Например, если ребёнок хочет закончить партию побыстрее, он может завершить цепочку партии уже на шестой позиции. С другой стороны, каждый ученик теперь должен сам следить за соблюдением правил игры, в частности за соблюдением очерёдности хода, за тем, чтобы на каждом ходу появлялся только один отрезок и за тем, чтобы все ходы аккуратно переносились с предыдущей позиции на следующую.

Провести проверку поможет указание. Действительно, если некоторая позиция заключительная, то либо есть одноцветный треугольник, либо все точки на окружности соединены. Первое проверить достаточно просто. Если в предыдущей задаче вы обсуждали с ребятами, сколько отрезков на окружности с пятью точками должно выходить из каждой точки в случае ничьей, то достаточно просто посчитать это в заключительной позиции, если нет, можно обсудить вопрос о числе отрезков в этой задаче.

Мы приводим один пример цепочки игры с заданным началом, в которой каждый из игроков стремился к выигрышу:

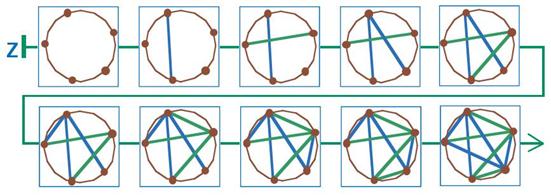
Задача 36. Эта задача сложнее, чем задача 35. Здесь нужно сначала спланировать решение на черновике (например, на пустом поле на листе вырезания) и только потом построить цепочку позиций, воспользовавшись заготовками на листе вырезания. Нужно вспомнить правила игры, понять, какая позиция будет выигрышной для Второго — это треугольник из синих отрезков (так как Второй выигрывает, когда проигрывает Первый). Одни дети могут строить решение этой задачи довольно долго, другие могут найти простое решение сразу. И тот и другой случай представляет определённый интерес.

Короткое решение основывается на том, что Первый может стремиться к проигрышу, а Второй просто не будет ему мешать. При таком подходе ясно, что очередной ход Второго может быть почти любым, а следующий ход Первого замыкает треугольник, что приводит к его проигрышу:

Это простое построение не смогут провести дети, которые захотят, чтобы Первый играл правильно, разумно, не поддавался и т. п. Таким образом, здесь есть что обсудить и в чём разобраться. Если будет время, предложите детям самим поиграть в «сим» с данным началом игры (можно опять-таки использовать пустые поля на листе вырезания, которые мы специально заготовили с запасом). Затем можно собрать заключительные позиции разных партий, в которых выиграл Второй, и обсудить их.

Вот одна из цепочек игры с разумной игрой обоих игроков:

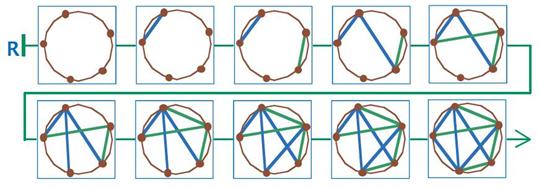
Задача 37. По содержанию эта задача наиболее близка к задаче 28, но в отличие от неё является обязательной. Вполне возможно, что некоторым учащимся понадобится ваша помощь. Большинство ребят, скорее всего, будут решать задачу методом проб и ошибок — строить ломаную ползунка случайным образом, как получится. Лучше всего сначала делать это на запасных полях на листе вырезания.

Соображения, приведённые в задаче 28 о соотношении числа звеньев ломаной (т. е. числа ходов) и точек на поле, через которые прошёл ползунок, позволяют сделать вывод, что в заключительной позиции цепочки W ползунок должен пройти через все 12 точек поля, а в заключительной позиции F — через 11 точек поля. Хорошо, если сильные ребята постепенно будут усваивать подобные закономерности. При этом всем ребятам необходимо понимание того, что число сделанных ходов определяет число звеньев ломаной ползунка. Таким образом, вам, проходя по классу, достаточно будет обратить внимание учащегося на то, что построенная им ломаная не соответствует требуемому числу ходов.

Ответ: подходящих цепочек много. Мы приводим одну цепочку W и одну цепочку F:

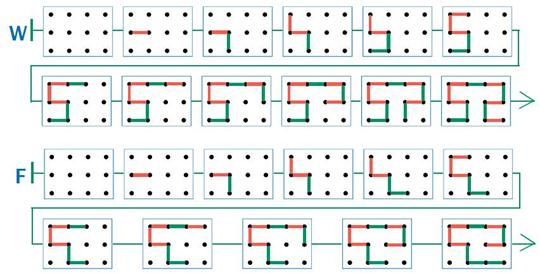
Задача 38. Необязательная. Если вы хотите предложить эту задачу слабым учащимся, лучше заранее сделать несколько копий фигурок из этой задачи. Тогда можно посоветовать ребятам вырезать фигурки и составить цепочку на столе, передвигая фигурки. Строим сначала несколько фрагментов цепочки, например: «крокодил — слон», «тигр — слон — жираф» (этот фрагмент строим с конца). Потом построенные фрагменты объединяем в одну цепочку.

Задача 39. Необязательная. Подобная задача ребятам уже встречалась (см. комментарий к задаче 29). Поэтому данную задачу можно использовать для повторения и обобщения на более сложном уровне. Например, если, решая задачу 29, ребята писали цепочки партий формально, попросите их здесь составлять цепочки честной игры, где ни один игрок не поддаётся и каждый пытается выиграть (впоследствии мы назовём такую партию разумной). Для этого лучше всего подойдёт игровой вариант решения — сыграть с соседом несколько партий в «камешки» по данным в задаче правилам и обобщить закономерные игровые ситуации. В ходе игры станет ясно, что если Первый на первом ходу взял 3 камешка, то Второй при честной игре на втором ходу возьмёт 3 оставшихся камешка и выиграет. Если же Первый на первом ходу возьмёт 4 камешка, то Второй проиграет в любом случае. Если же Первый на первом ходу берёт 1 камешек, то игра может сложиться по-разному, в зависимости от следующего хода Второго. Можно проводить обобщение и в другом направлении. Например, спросить у ребят, можно ли по длине цепочки партии сразу определить победителя. Да, если цепочка чётной длины, то выигрывает Первый, если нечётной — Второй. Значит, задача сводится к тому, чтобы написать две цепочки игры — чётной и нечётной длины.

Урок «Выигрышная стратегия. Выигрышные и проигрышные позиции»

Постепенно мы переходим от формальной работы с цепочками партий к их содержательному анализу. Действительно, до этого момента учащиеся составляли цепочки партий, соблюдая только правила игры и, возможно, некоторые условия (выигрыш определённого игрока, определённую длину цепочки, данную заключительную позицию и пр.). При этом ребята совершенно не должны были задаваться вопросами, насколько вероятно проигрывание такой партии в жизни и насколько умело и старательно играют Первый и Второй. Чтобы соблюсти условия задачи, при построении цепочки партии ребята могли и подыгрывать определённому игроку, заставляя противника играть неразумно, поддаваться. Всё это мы уже отмечали раньше, равно как и то, что некоторые ребята всё же будут стараться построить цепочку честной (разумной) партии, считая ситуацию формального построения цепочки партии неестественной.

Теперь пришло время выделить из множества всех возможных партий разумные партии, т. е. такие, в которых каждый игрок стремится к победе и не поддаётся противнику (при этом, конечно, играет честно, соблюдает правила игры). Это значит, что если игрок может с помощью некоторого хода (или серии ходов) выиграть, то он в разумной партии сделает именно этот ход (или серию ходов).

Возьмём сначала самую простую игру — «камешки». В этой игре возможных позиций немного, и они легко упорядочиваются — укладываются на отрезок числовой прямой от нуля до начальной позиции игры. Начнём с самого простого — изучения отдельных позиций: какие из них являются выигрышными, а какие — проигрышными. На самом деле мы изучаем не собственно позицию, а всю игру с этой начальной позицией. Но на начальных этапах рассмотрения позиции количественно до того небольшие, что говорить об игре сложно: она тривиальна и заканчивается, практически не успев начаться.

Что же означает выражение «изучить позицию»? Это значит выяснить, сможет ли выиграть из этой позиции тот игрок, чья очередь ходить. При этом нужно рассмотреть все возможные варианты ответных ходов противника. Обратите внимание, что мы теперь не говорим о Первом и Втором игроках. Пока неважно, какому именно игроку досталась рассматриваемая позиция — Первому или Второму. Важна только выигрышность позиции с точки зрения игрока, чей черёд делать ход.

Для рассмотрения на листе определений выбрана игра «камешки», в которой разрешено брать 1, 3 или 4 камешка на каждом ходу (такой набор разрешённых ходов не случаен: при более простых разрешённых ходах раскраска числовой линейки получается периодической, и это может привести детей к нежелательным обобщениям).

Начнём изучение с совсем маленьких начальных позиций. Если камешки уже кончились (рассматриваемая позиция — 0), то игрок, который только что сделал ход, выиграл. Это значит, что для игрока, которому теперь надо было бы сделать ход, позиция 0 — проигрышная. Он точно не выиграет, потому что его противник уже выиграл!

Если камешков 1, 3 или 4, то тот игрок, чья очередь ходить, может сделать выигрышный ход — просто забрать все камешки. Значит, эти позиции выигрышные в нашей игре.

Если камешков 2, то игрок, чья очередь ходить, может сделать только один ход: взять 1 камешек. При этом он обязательно проиграет в этой партии: его противник заберёт оставшийся камешек и выиграет. Значит, позиция 2 — проигрышная.

Перейдём теперь к позициям с большим числом камешков. Здесь понадобится провести некоторые рассуждения. Представим себе, что мы играем в камешки и стремимся к победе. Чтобы победить (независимо от того, какие ходы будет выбирать противник), нам надо постараться поставить нашего противника в невыгодное положение. В идеале хорошо было бы сыграть так, чтобы противнику просто некуда было деться: какой ход он ни сделает, все равно останется в проигрыше (помните, в задаче 15 мы обсуждали подобную ситуацию, когда получалась вилка для Второго игрока, ставящего нолики). Что это значит в нашем случае? Это значит, что надо оставить противнику такую позицию, из которой при любом его ходе нам достанется выигрышная позиция.

Назовём проигрышной позицию, любой разрешённый ход из которой ведёт в выигрышную позицию. Назовём выигрышной позицию, из которой существует ход, приводящий в проигрышную позицию.

Итак, если игроку нужно делать ход из выигрышной позиции, он всегда сможет подобрать такой ход, который оставит противнику проигрышную позицию. Любой ход противника из этой (проигрышной) позиции оставит нашему игроку выигрышную позицию. Значит, он опять сможет выбрать ход, в результате которого позиция изменится на проигрышную, и т. д. В итоге игрок выиграет в этой партии, как бы ни старался противник.

Продолжим исследования позиций в игре «камешки», следуя данным определениям. Из позиций 5 и 6 есть ход, в результате которого получается проигрышная позиция 2. Значит, позиции 5 и 6 — выигрышные позиции. В результате всех ходов из позиции 7 получаются выигрышные позиции, значит, позиция 7 — проигрышная позиция и т. д.

Что же такое разумная партия с точки зрения уже введённых определений выигрышной и проигрышной позиций? Это такая партия, в которой на каждом ходу игроки стараются по возможности оставить противнику проигрышную позицию. Если игроку досталась выигрышная позиция, то он наверняка сможет оставить противнику проигрышную. Однако если игрок делает ход из проигрышной позиции, то соблюсти это правило точно невозможно, как бы он ни старался (ведь всякий ход из проигрышной позиции оставляет противнику выигрышную позицию). Таким образом, на самом деле разумно может вести себя только игрок, который делает ход из выигрышной позиции. Если такой игрок на протяжении всей игры делает только разумные ходы, то в дальнейшем мы будем говорить, что он следует своей выигрышной стратегии. Его противник может при этом делать любые ходы, партия всё равно будет оставаться разумной.

Конечно, обсуждение этих моментов не нужно проводить со всем классом на первом уроке по теме. Главное, что должны понять дети после изучения листа определений, — чем выигрышная позиция отличается от проигрышной. Также они должны уметь раскрашивать позиции на числовой линейке и понимать, что в разумной партии игрок, у которого есть возможность, всегда должен делать такой ход, который оставит противнику проигрышную позицию.

Выигрышные и проигрышные позиции существуют и в других играх. Но изучение других игр связано с дополнительными трудностями. Так, в отличие от игры «камешки» в играх «ползунок», «сим», «крестики-нолики» все возможные позиции придётся размещать на дереве игры, которое чаще всего будет очень большим, поэтому возникают технические трудности. В игре «камешки» позиции Первого и Второго ничем не отличаются, поэтому можно говорить, что некоторая позиция является выигрышной или проигрышной для игрока, который должен делать из неё ход, и анализировать игру «камешки» одновременно как для Первого, так и для Второго (в отличие, например, от игры «крестики-нолики», в которой каждый игрок изменяет позицию по-своему, ставит свой знак, и поэтому каждую позицию нужно анализировать для каждого игрока в отдельности).

Решение задач 40—48 из учебника

Задача 40. Первое задание данной задачи — продолжение работы, начатой на листе определений. Поэтому ребятам помогут те же рассуждения, которые приведены на с. 27 — 28 учебника. Начинаем со следующей нераскрашенной позиции — позиции 9. Возможные ходы игры — 1, 3 и 4, следовательно, из позиции 9 могут получиться позиции 8, 6 и 5. Все они выигрышные, значит, позиция 9 проигрышная. Если кто-то из ребят испытывает трудности, поработайте вместе над позицией 9, используя наводящие вопросы: «Какие ходы может сделать игрок?», «Какие позиции могут получиться из позиции 9 в результате одного хода?», «Какими являются эти позиции (есть ли среди них проигрышные)?», «Какой (выигрышной или проигрышной) является позиция 9?».

Далее ребята продолжают раскрашивать числовую линейку самостоятельно до позиции 15:

Теперь, пользуясь раскрашенной числовой линейкой, учащиеся отвечают на вопросы, подводящие к пониманию поведения игроков в разумной партии. Как говорилось на листе определений, в разумной партии игрок всегда старается оставить противнику проигрышную позицию. Здесь же требуется подобрать такие ходы, которые могут быть в разумной партии.

Наконец, ребята должны составить разумную партию целиком. Мы уже обращали ваше внимание, что разумный ход (оставляющий противнику проигрышную позицию) может сделать лишь игрок, находящийся в выигрышной позиции. Поскольку игру начинает Первый и находится при этом в выигрышной позиции 15, то он может сделать разумный ход: взять 1 камешек и оставить Второму проигрышную позицию 14. Теперь в результате любого хода Второй оставит Первому выигрышную позицию (13, 11, 10). Второй просто не может сделать позицию проигрышной, поэтому он может делать любой ход, например взять 3 камешка. Первый снова должен сделать разумный ход и оставить Второму проигрышную позицию 7 и т. д. Итак, в данном случае разумной партию делает только Первый, все позиции, которые он оставляет Второму, должны быть проигрышными. Например, разумной будет следующая партия:

15 — 14 — 11 — 7 — 3 — 0.

Задача 41. Данная задача аналогична задаче 40, и работать с ней ребятам предстоит по той же схеме. Вот раскрашенная числовая линейка:

Существенное отличие обнаруживается лишь при выполнении последнего задания — написания цепочки разумной партии. Действительно, начальная позиция 12 — проигрышная, значит, Первый в начальной позиции не сможет сделать разумного хода: в результате любого его хода Второй получает выигрышную позицию. Зато Второй, оказавшись в выигрышной позиции, может сделать разумный ход — оставить противнику проигрышную позицию и поступать таким образом до конца партии, которая в этом случае закончится его победой. Вот одна из возможных разумных партий:

12 — 11 — 9 — 7 — 6 — 5 — 3 — 1 — 0.

Задача 42. Необязательная. Эта задача помечена как необязательная, хотя её первое задание ничем не сложнее обязательной задачи 40. Вот раскрашенная числовая линейка, которая должна появиться у ребят:

Однако ответ на вопрос потребует от ребят дополнительных размышлений и даже некоторого забегания вперёд — подобные вопросы мы будем обсуждать со всеми детьми позднее. Из материала листа определений и решения задачи 40 становится ясно, что игрок, находящийся в выигрышной позиции, может (делая до конца партии только разумные ходы) выиграть. Однако если он не будет делать разумные ходы, то может и проиграть. Обратите внимание, что в вопросе речь идёт не о разумной партии, а вообще о любой партии.

Проведя несколько партий в камешки по данным правилам (начальная позиция 11, разрешается брать 1 или 3 камешка), ребята могут убедиться в том, что выигрывает действительно всегда только Первый. Почему? Анализируя раскрашенную линейку, можно заметить, что Первый вынужден играть разумно, т. е. он при любом своём ходе оставляет Второму только проигрышные позиции. Это легко проверить, моделируя различные партии на раскрашенной числовой линейке.

Ещё проще можно объяснить исход игры, используя чётность и нечётность позиций. Действительно, при начальной позиции 11 (нечётное число) все возможные позиции после хода Первого — чётные числа (ведь разрешается брать только 1 или 3 камешка). А после хода Второго остаются всегда только нечётные числа. Поэтому позиция 0 может получиться только после хода Первого (0 — чётное число), а после хода Второго позиция 0 получиться не может.

Задача 43. Необязательная. Если у кого-то из ребят возникли трудности с решением, попробуйте с помощью вопросов навести его на мысли о связи длины ползунка (чётности или нечётности числа его звеньев) и выигрыша определённого игрока (см. комментарии к задачам 27, 28, 37). Посоветуйте ребятам сначала работать на черновике (на запасных полях 4 × 3 на листах вырезания), а уже потом нарисовать соответствующие позиции в рабочей тетради. Лучше, если ходы Первого и Второго ребята будут, как обычно, раскрашивать двумя разными цветами, так им проще будет увидеть победителя, а вам будет проще проверить правильность ответа.

Задача 44. Необязательная. Скорее всего, дети воспользуются методом проб и ошибок или методом перебора. Проще всего узнать первую команду в первой конструкции повторения, так как команда «вправо» — это единственная команда, которую может выполнить Робик из начального положения, не выходя за пределы закрашенной фигуры. Вторую команду можно определить перебором. Действительно, команду «вниз» Робик выполнить не может (тогда он выйдет за пределы поля), команду «вправо» — может, но тогда Робик не сможет повторить команды внутреннего цикла даже дважды. Остаются две возможные команды — «влево» и «вверх», которые надо рассмотреть подробнее. Выбрав команду «вверх», подберём число повторений (здесь возможны два варианта — 2 и 3). Сравнивая на каждом этапе результат выполнения конструкции с клетками, закрашенными в задании, постепенно находим правильный ответ. Закончить решение задачи, конечно, необходимо проверкой — выполнением написанной программы на таком же поле (можно использовать поля на листе вырезания).

Ответ:

ПОВТОРИТЬ 3 РАЗА

вправо

вверх

КОНЕЦ

ПОВТОРИТЬ 3 РАЗА

влево

КОНЕЦ

ПОВТОРИТЬ 3 РАЗА

вниз

вправо

КОНЕЦ

Задача 45. Данная задача — обобщённый и сокращённый вариант задач 40 и 41, но уже не содержащий подсказок. Вот раскрашенная числовая линейка:

Здесь не указано, кто должен победить в разумной партии. Учащийся должен понять это сам, анализируя выигрышные и проигрышные позиции на числовой линейке. В данном случае начальная позиция 15 — выигрышная, поэтому разумность партии зависит от Первого, который должен в результате каждого своего хода оставлять Второму проигрышную позицию. Ходы Второго могут быть любыми. Если задачи 40 и 41 ребята решили легко, данную задачу можно использовать для промежуточного контроля. Здесь можно проверить, научились ли ребята самостоятельно раскрашивать числовую линейку и понимают ли они отличие разумной партии от других. Ниже приведена одна из возможных разумных партий:

15 — 12 — 9 — 8 — 6 — 4 — 2 — 0.

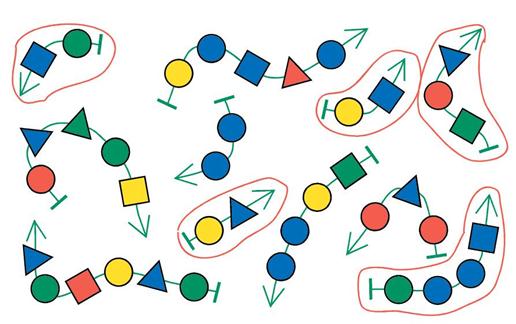
Задача 46. В ходе решения этой задачи ребята повторяют понятие уровней дерева. Однако самым сложным здесь оказывается обеспечить истинность утверждения в рамке, потому что бусины из мешков A, B, C, D можно просто нарисовать сразу на соответствующих уровнях.

Как же соединить эти бусины в дерево, чтобы в нём не было двух одинаковых путей? В данной задаче ситуация осложняется тем, что на каждом уровне есть несколько одинаковых бусин. В ходе проб и ошибок ребята могут заметить, что никакая бусина третьего уровня не может иметь две (или более) следующие, поскольку в этом случае в дереве сразу появятся одинаковые пути, потому что все бусины четвёртого уровня — одинаковые. Следовательно, каждая бусина третьего уровня должна иметь не более одной следующей. Из этого следует, что ровно одна бусина третьего уровня является листом. Лучше сделать листом жёлтую круглую бусину, чтобы уменьшить число одинаковых бусин, которые будут входить в пути длины 4. Соединим оставшиеся бусины третьего и четвёртого уровней. Теперь у нас появились два одинаковых конца пути (желтая круглая — зелёная круглая). Учитывая то, что первые бусины этих путей будут также одинаковыми (потому что все бусины первого уровня одинаковые), мы можем поправить дело только за счёт бусин второго уровня — взять в эти пути разные бусины второго уровня (красную квадратную и синюю треугольную). Правильный ответ в этой задаче не единственный, мы приводим лишь один вариант дерева Х:

Задача 47. Здесь при построении каждой цепочки требуется соблюдение двух условий: ползунок должен проходить через заданный отрезок, выиграть должен определённый игрок. Первое условие соблюсти достаточно легко — надо просто пристраивать ходы к заданному отрезку. Что касается второго условия, здесь могут помочь некоторые соображения, касающиеся связи между выигрышем определённого игрока и чётностью или нечётностью числа звеньев ползунка. Ясно, что, если число звеньев ползунка чётное, выиграет Второй, если нечётное — Первый. Кроме того, число звеньев ползунка связано с числом точек на поле, через которое он прошёл: ползунок из нечётного числа звеньев проходит через чётное число точек, и наоборот. Таким образом, чтобы выиграл Второй, нужно, чтобы ползунок прошёл через все 9 точек поля, а чтобы победу одержал Первый — через 8 или 6 (других вариантов на данном поле не может быть). Если кто-то из ребят будет строить ползунок наугад и запутается, натолкните его на подобные соображения. Ниже мы приводим два примера цепочки К и один пример цепочки Л.

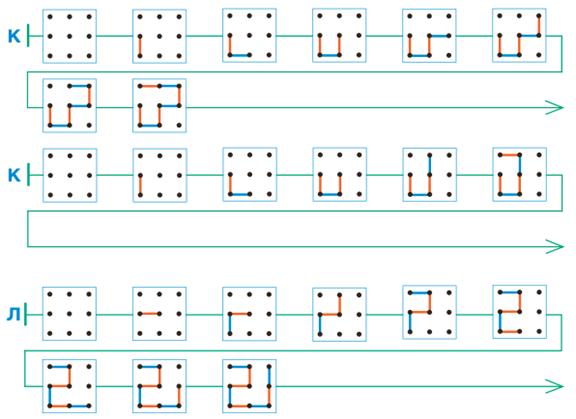
Задача 48. Необязательная. В курсе 2 класса с такими задачами ребята уже встречались. Сложности здесь могут быть связаны с логической структурой условия. В частности, нужно понимать, что любое слово из мешка должно находиться в словарике, но в словарике есть и лишние слова, которые для решения не пригодятся. Каждая заготовка в мешке однозначно определяет слово, которое должно быть в неё помещено. Например, в словарике есть лишь одно слово из четырёх букв (ГУСЬ), именно его нужно вписать в заготовку из четырёх окон в мешке. То же относится и к другим словам, в том числе содержащим дефис. Так, в словарике есть лишь 2 слова, составленные из двух слов, которые пишутся через дефис, в первом из которых четыре буквы, а во втором — шесть. При этом лишь одно из этих слов заканчивается на букву К. Поэтому заготовка для первого слова в мешке определяет его однозначно (ОРЁЛ-КАРЛИК).

Уроки «Выигрышные стратегии в игре «камешки»

Работая с предыдущей темой, ребята анализировали в основном отдельные позиции игры «камешки» (и ходы, приводящие к ним). Теперь настало время проанализировать ход игры в целом. Перекидным мостиком между двумя этими темами является понятие разумной партии (и разумного хода). Мы уже выяснили, что в разумной партии каждый игрок должен стараться следовать общему правилу — всегда оставлять противнику проигрышную позицию. В ходе решения задач ребята могли заметить, что в одной партии игры «камешки» только один из игроков может следовать этому правилу — тот, кто первым сможет занять выигрышную позицию. Теперь мы будем говорить, что такой игрок имеет выигрышную стратегию. Если он будет следовать ей, а значит, делать только разумные ходы и оставлять противнику только проигрышные позиции, то выиграет при любой игре противника.

Итак, если игрок, имеющий выигрышную стратегию, будет следовать ей, то все возможные такие партии будут только разумными. Если начальная позиция выигрышная, то выигрышную стратегию имеет Первый, если проигрышная — Второй. Изложенное общее правило выигрыша — стараться оставлять противнику проигрышную позицию — в каждой игре «камешки» реализуется по-разному. Раскраска клеток числовой линейки определяет как игрока, обладающего выигрышной стратегией, так и его ходы (следование выигрышной стратегии). Правило выигрыша может быть сформулировано либо в виде последовательности ходов, которые должен делать игрок, либо в виде правила о том, какие позиции должен оставлять противнику данный игрок (если проигрышные позиции подчиняются некоей общей закономерности). В следующих задачах ребятам предстоит сформулировать выигрышные стратегии в виде правила.

Решение задач 49—62 из учебника

Задача 49. Изучая данный материал, ребята должны понять: выигрышная стратегия действительно помогает выиграть одному из игроков и нужно научиться ей следовать. Именно поэтому мы начинаем серию задач на эту тему с небольшого соревнования. Разрешённые ходы игры такие же, как на листе определений (1 и 2 камешка). Для следования выигрышной стратегии ребята используют раскрашенную числовую линейку с листа определений на с. 32, поэтому лучше посоветовать им не выбирать начальную позицию больше 10. Первое, что говорит о понимании ребятами материала листа определений: Первый выбирает в качестве начальной позиции выигрышную. В противном случае учащемуся надо посоветовать ещё раз прочитать материал листа определений. Второе условие правильного выполнения задания — все сыгранные партии должны быть разумными, т. е. в цепочке партии все позиции, получающиеся после ходов Первого, — проигрышные. Чтобы вам легче было проверить соблюдение этих двух условий, попросите ребят записывать на черновике цепочки всех сыгранных партий. Если в каждой партии Первый действительно следует выигрышной стратегии, то оба утверждения в рамках должны быть истинными. С теми парами учащихся, у которых так не получилось, можно порассуждать вместе. Эта задача является важным шагом при переходе от формального анализа отдельных позиций к содержательному анализу реальной игры.

Задача 50. В этой задаче проверяется понимание ребятами материала второй части листа определений — формулирования выигрышной стратегии в виде общего правила. Для начала стоит внимательно посмотреть на раскрашенную числовую линейку и выяснить, какой закономерности подчиняется размещение проигрышных позиций. Так, видно, что на линейке существует чёткое чередование позиций — проигрышная, две выигрышные, проигрышная, две выигрышные и т. д. Более того, все проигрышные позиции — числа, которые делятся на 3. Именно такие позиции должен оставлять противнику игрок, который первым сможет занять выигрышную позицию. В данном случае начальная позиция — число, которое делится на 3, это проигрышная позиция, значит, первым в выигрышной позиции окажется Второй и выигрышная стратегия имеется у него.

Задача 51. Здесь проверяется, может ли учащийся применить полученную в предыдущей задаче выигрышную стратегию для построения разумной партии игры. На предыдущем уроке ребята уже строили такие партии, но только с опорой на раскрашенную линейку. Здесь ребёнок может использовать начало такой линейки и правило выигрышной стратегии. Так, в данной задаче начальная позиция на 3 не делится, значит, она выигрышная и выигрышную стратегию имеет Первый. Первая ближайшая проигрышная позиция — 24 камешка, значит, первый ход Первый должен сделать именно в неё. Дальше Первый продолжает делать ходы только в проигрышные позиции: 21, 18, 15 и т. д.

Задача 52. На листе определений данная игра «камешки» (с ходами 1, 2 и 3 и любой начальной позицией) обсуждена исчерпывающе — сформулировано правило выигрышной стратегии, которое позволяет для любой начальной позиции определить обладателя выигрышной стратегии и научить его обыгрывать своего соперника. В частности, это правило позволяет легко раскрасить числовую линейку, ответить на вопросы и построить разумные партии. Тем не менее кто-то из ребят будет решать задачу так же, как на предыдущем уроке. Таких учеников не надо останавливать, для них это будет дополнительной возможностью повторить материал. Если вам важно, чтобы и эти дети в этой задаче использовали сформулированную на листе определений выигрышную стратегию, предложите им по окончании решения большие начальные позиции, для которых раскрасить числовую линейку будет затруднительно.

Задача 53. Данная задача напоминает задачу 49. Разница в том, что здесь детям предлагается играть партии без опоры на числовую линейку, используя только правила выигрышной стратегии (сформулированного на листе определений), именно поэтому начальные позиции должны быть больше 20. Кому-то это может показаться сложным. Критерии правильности работы учащихся описаны в комментарии к задаче 49. Если вы видите, что Первый всё же проигрывает, порассуждайте вместе с ним, опираясь на материал уже решённых задач 49—52. Особенно стоит обратить внимание на построение разумной партии игры в задаче 51.

Задача 54. Здесь ребята вспоминают тему «Конструкция повторения» и ситуацию вложенного цикла.

Ответ:

Задача 55. Эта задача полностью аналогична тем, которые ребята решали на предыдущем уроке. Предоставьте учащимся достаточно времени, чтобы они могли справиться с ней самостоятельно. Данную задачу удобно использовать для текущего контроля предыдущей темы.

Задача 56. Задача на повторение лексики, относящейся к цепочкам, в частности понятий «раньше/позже» и «перед каждой/после каждой». Сначала удобно использовать второе утверждение и найти место для буквы К. Эта буква будет первой в слове. Теперь попробуем найти место для трёх букв О. У нас имеется 5 пустых окон. В одном из них (после буквы Ы) буква О стоять не может. Также две буквы О не могут идти подряд (иначе не будет истинным первое утверждение). Значит, одна буква О стоит в последнем окне, а две другие — во втором и четвёртом окнах. Теперь используем последнее утверждение и получаем слово КОРОМЫСЛО.

Задача 57. Эта задача уже на новый лист определений. Раскрасив в задаче 55 числовую линейку, ребята замечают, что все позиции, делящиеся на 3, — проигрышные, а все остальные — выигрышные. Поэтому при начальной позиции 212 камешков выигрышную стратегию имеет Первый. Он должен всегда забирать столько камешков, чтобы Второму оставалось число камешков, кратное трём. Так, на своём первом ходу Первый должен забрать 2 камешка и оставить Второму позицию 210 камешков.

Задача 58. Необязательная. Задача, аналогичная задаче 53. Проведение соревнования, как обычно, потребует некоторого дополнительного времени. Поэтому при дефиците времени данную задачу можно пропустить.

Задача 59. Необязательная. Здесь ребята повторяют лист определений «Перед каждой, после каждой», а также лист определений «Если бусины нет». Можно сразу отбросить (например, вычеркнуть) те цепочки, где круглая бусина — последняя (у неё «первой бусины после» вообще нет), таких цепочек оказывается 4. Из оставшихся семи подходят лишь 5 цепочек, причём в четырёх из них круглая бусина одна (возможно, кто-то из ребят забыл о том, что конструкцию «после каждой» можно употреблять и в этом случае).

Ответ:

Задача 60. Необязательная. Задача на повторение темы «Все пути дерева». Проверьте, что все помнят алгоритм построения всех путей дерева, который детально рассматривался в курсе 2 класса. Лучше всего, если ученик использует при этом некоторую систему пометок. Мы советовали помечать каждый лист, после того как выписан ведущий в него путь. Хорошо также, если ученик имеет систему перебора листов (например, сверху вниз). Особое внимание необходимо обратить на детей, которые выписывают пути как попало и при этом делают ошибки.

Ответ:

МЕЛ

МЕЛЬ

МЕХ

МЕЧ

МОЗГ

МОЛ

МОСТ

МОХ

СОМ

СОЛО

СОЛЬ

Задача 61. Три команды, уже заданные в программе, дают ребятам ключ к решению, поскольку на поле имеется лишь одна клетка, из которой Робик, не выходя за пределы закрашенной фигуры, может выполнить серию команд «вниз» — «вверх» — «вверх»: это центральная клетка второй строки. Следующий вопрос, который нужно решить детям: из какой клетки Робик начинал свой путь, если он добрался до упомянутой выше клетки за четыре команды? При этом нужно учитывать фигуру, которую закрасил Робик в процессе выполнения программы, — нельзя выходить за её пределы. Клетку положения Робика на поле в начальной позиции можно искать перебором. Таких возможных клеток оказывается две: вторая и шестая клетки второй строки. Отсюда возможных программ Т тоже две.

Ответ:

вниз

вверх

вправо

вправо

вниз

вверх

вверх

вниз

вправо

вправо

вниз

Или:

вниз

вверх

влево

влево

вниз

вверх

вверх

вниз

влево

влево

вниз

Задача 62. Необязательная. Сложность данной задачи в том, что фигурки похожи. Все они звёзды, которые различаются только числом лучей. Чтобы не сбиться, полезно считать число лучей. Можно использовать деление звёзд на группы с одинаковым числом лучей по ходу решения. Например, в левом мешке всего две пятиконечные звезды — синяя и зелёная. Найдём пятиконечные звёзды в правом мешке. Их две и обе они нераскрашенные, значит, раскрасим одну из них в синий цвет, а другую — в зелёный. Лучше сразу после этого соединить одинаковые пятиконечные звёзды в пары. После этого можно перейти к шестиконечным звёздам и т. д.

Проект «Мой доклад» (только для компьютерного варианта изучения курса)

Практическая цель проекта — подготовка текста доклада и выступления на заданную тему с опорой на презентацию.

Методическая цель проекта — приобретение начальных навыков поиска информации в сети, приобретение умения работать с текстом, закрепление умения работы с программой презентаций, закрепление навыков работы с информацией (отбор, структурирование, анализ и пр.), закрепление навыков выступления с графической опорой.

Дата добавления: 2015-01-03