Востоков Е.В. 2 страница

Таблица 1.16 Упорядочение рекламных кампаний по оценке разных маркетинговых групп

Уровень оценки стратегий
	Оценка
Рекламная кампания 1	МГ
	Накопленная оценка	0,2	0,425	0,6375	0,8125
	Оценка
Рекламная кампания 2	МГ
	Накопленная оценка	0,1875	0,3625	0,5625	0,775
	Оценка
Рекламная кампания 3	МГ
	Накопленная оценка	0,1875	0,3875	0,6	0,775
	Оценка
Рекламная кампания 4	МГ
	Накопленная оценка	0,2	0,4125	0,6375	0,825
	Оценка
Рекламная кампания 5	МГ
	Накопленная оценка	0,175	0,3875	0,575	0,8

Примечания: 1) Наихудшей оценке соответствует уровень упорядочения 1, а наилучшему 5

2) медианная оценка соответствует заштрихованным ячейкам.

В качестве наилучшей рассматривается рекламная кампания, имеющая максимальную медианную оценку. В нашем случае такой является 3-я альтернатива.

13. Оцените, насколько Ваше мнение совпало с результатами, полученными с помощью математических моделей принятия решений. Укажите, какие причины сказались на отклонении Вашего решения от полученного с помощью математических методов.

14. Обобщить все полученные результаты и оформить их в виде отчета

Лабораторная работа №2. Деловая игра «Страховка» (выбор в условиях стохастической неопределенности)

1. Лабораторная работа проводится в форме деловой игры. Студенческая группа разбивается на команды по 3 человека. Каждой команде выдается одинаковое задание, которое должно быть обсуждено в группе и принято однозначное решение.

2. В качестве задания рассматривается следующая ситуация:

Небольшая фирма имеет только 1 автомобиль, который нужно застраховать. Имеются следующие варианты страхования автомобиля:

· Полное страхование ущерба – вне зависимости от размера ущерба страховая компания выплачивает фирме возмещение;

· Страхование с лимитом страховой ответственности - страховая компания выплачивает фирме возмещение, если оно не превосходит предельную сумму;

· Страхование с возмещением пропорционально ущербу - вне зависимости от размера ущерба страховая компания выплачивает фирме фиксированную долю от возникшего ущерба;

· Страхование с условной франшизой - страховая компания выплачивает фирме возмещение в полном объеме, если ущерб превосходит минимальную сумму возмещения (франшизу);

· Страхование с безусловной франшизой - страховая компания выплачивает фирме возмещение в полном объеме за вычетом минимальной суммы возмещения (франшизы);

Стоимостные параметры предложенных страховых документов представлены в таблице 2.1.

Таблица 2.1. Основные параметры страховых инструментов (руб.)

	Стоимость годовой страховки	Лимит	Франшиза	Коэффициент пропорциональности
Безлимитная страховка
С лимитом страховой ответственности
Безлимитная страховка с возмещением пропорционально ущербу	11562,5			50%
Условная франшиза
Безусловная франшиза

В таблице 2.2. Представлены вероятностные и стоимостные характеристики страховых случаев, которые могут случиться с автомобилем

Таблица 2.2. Основные характеристики страховых случаев

	Отсутствие страховых случаев	Мелкая авария	Средняя авария	Крупная авария	Угон автомобиля
Ущерб
Вероятность случая в течение года	0,8	0,1	0,05	0,03	0,02

Считается, что в течение года может произойти только один страховой случай.

3. Обсуждение выбора страховки в студенческих группах из 3-х человек. Каждая группа выбирает только 1, наиболее предпочтительный по ее мнению вариант страхования.

4. Каждая из студенческих групп выступает со своим предложением о выбираемом варианте страхования и отвечает на вопросы рецензентов. Рецензирование строится по круговому принципу. (Решение 1-ой группы студентов рецензирует 2-я; решение 2-ой группы – 3-я, и т.д. Решение последней группы студентов рецензируется первой).

5. На основе обсуждения прямым голосованием выбирается наилучший, по мнению студентов, вариант страхования автомобиля.

6. Студентам предлагается обсудить вопрос, как изменится их решение, если у предприятия не 1 автомобиль, а 100.

7. Выбор решения строится по правилам, изложенным в п. 4. – 6.

8. После принятия решений студентами проводится анализ решений с помощью математических методов принятия решений

Для этого строится матрица ущербов

Таблица 2.3. Матрица ущербов и компенсаций (руб.)

	Отсутствие страховых случаев	Мелкая авария	Средняя авария	Крупная авария	Угон автомобиля	Среднее
Вероятность страхового случая	0,8	0,1	0,05	0,03	0,02
Безлимитная страховка	-25625	-5625				-5125
С лимитом страховой ответственности	-13125					-3625
Безлимитная страховка с возмещением пропорционально ущербу	-11562,5	-1562,5	13437,5	88437,5	238437,5	-1312,5
Условная франшиза	-18400	-18400
Безусловная франшиза	-18150	-18150				-1650

8.1. Когда страхуется только 1 автомобиль, мы сталкиваемся с ситуацией однократного решения. В этой ситуации находится состояние, имеющее наибольшую вероятность возникновения при выборе той или иной страховки (т.е. определяется мода распределения). В качестве наиболее вероятного состояния будет отсутствие страховых случаев. Следовательно, рекомендуется выбрать страховку, которая в случае отсутствия страховых случаев, имеет наименьшую стоимость. Такой, в нашем примере, оказывается страховка с пропорциональным возмещением ущерба, которая стоит только 11562,5 рубля

8.2. В случае страховки 100 автомобилей мы имеем ситуацию многократного выбора, так как:

· Страхуется достаточно большое число объектов, страхование каждого из которых рассматривается как независимый случай. Более того, вероятность того, что ни с одним автомобилем ничего не произойдет, составляет 0,8¹⁰⁰, т.е. практически равна 0.

· Стоимость ни одной страховки не составляет более 6% от максимального страхового случая.

Таким образом, мы имеем классическую задачу многократного стохастического выбора. В этой ситуации применяется модель принятия решений на основе нахождения математического ожидания (среднего), которое определяется как

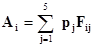
где F_ij – выигрыш компании при выборе i-го варианта страхования и наступлении j-го страхового случая; p_j – вероятность возникновения j-го страхового случая.

В соответствии с теорией, в качестве наилучшей рассматривается стратегия, обеспечивающая максимальное математическое ожидание (среднее). Наибольшее среднее обеспечивает страховка с условной франшизой, которая и должна быть выбрана при страховании автопарка.

9. Оцените, насколько Ваше мнение совпало с результатами, полученными с помощью математических моделей принятия решений. Укажите, какие причины сказались на отклонении Ваших решений от полученных с помощью математических методов.

10. Обобщить все полученные результаты и оформить их в виде отчета

Лабораторная работа №3. Деловая игра «Монетки» (Выбор в условиях антагонистического конфликта)

1. Лабораторная работа проводится в форме деловой игры. Студенческая группа разбивается на команды по 2 человека. Каждой команде выдается одинаковое задание.

2. В качестве задания рассматривается следующая ситуация: Каждой группе выдается комплект из 5 монет разного достоинства. Чем больше достоинство монеты, тем она крупней. В течение 1 раунда один из студентов выбирает 4 монетки разного достоинства, которые помещаются в закрытый контейнер. Второй игрок имеет право вытащить (не глядя) 2 или 3 монеты. Количество монет, вынимаемых из контейнера, объявляется вторым участником до начала вытаскивания монет. Вытаскивание 2-х монет является бесплатным. Стоимость вытаскивания 3-ей монеты составляет заранее заданную величину. Правила выигрыша следующие:

· Если вытаскиваются две монеты, то в случае, если суммарная стоимость вытащенных монет составляет более 70%, выигрывает вытащивший монеты игрок и его выигрыш составляет половину суммы, положенной в контейнер. Если совокупная стоимость, вытащенных монет составляет менее 70%, то второй игрок выплачивает первому половину суммы, положенной в контейнер.

· Если вытаскиваются три монеты, то в случае, если суммарная стоимость вытащенных монет составляет более 60%, то вытаскивающий монеты игрок выплачивает первому игроку сумму, равную суммарной стоимости монет положенных в контейнер. Если совокупная стоимость, вытащенных монет составляет не более 60%, то первый игрок выплачивает второму всю сумму, положенную в контейнер

3. По итогам раунда первый из игроков записывает выбранную комбинацию монет, и свой проигрыш или выигрыш в таблицу

Таблица 3.1. Пример таблицы, заполняемой первым игроком

Раунд	Комбинация монет	Стратегия противника	Выигрыш/ Проигрыш
Раунд 1	1, 2, 3, 4
Раунд 3	1, 2, 3, 4		-6
Раунд 5	1, 2, 3, 7		-6,5
Раунд 7	1, 2, 4, 7
Раунд 9	1, 3, 4, 7		-7,5
Раунд 11	2, 3, 4, 7		-12
Раунд 13	1, 2, 3, 7		-6,5
Раунд 15	1, 2, 3, 4		-6
Раунд 17	1, 2, 4, 7		-7
Раунд 19	1, 3, 4, 7
Итого			-25,5

Второй игрок записывает количество монет, которое он вытаскивал из контейнера и свой выигрыш.

Таблица 3.2. Пример таблицы, заполняемой первым игроком

Раунд	Количество монет	Выигрыш/ Проигрыш
Раунд 1		-5
Раунд 3
Раунд 5		6,5
Раунд 7		-10
Раунд 9		7,5
Раунд 11
Раунд 13		6,5
Раунд 15
Раунд 17
Раунд 19		-11
Итого		25,5

4. Игроки меняются ролями, т.е. в следующем раунде монеты кладет, тот который в предыдущем раунде вытаскивал монеты, а выбирает тот, который до этого клал монеты в контейнер.

5. Проводится 20 раундов выбора (По 10 раз в разных ролях).

6. По итогам игры заполняется следующие таблицы

Таблица 3.3. Выбор комбинаций, которые использовал студент, когда действовал как первый игрок

Комбинация монет	Число раз использования	Вероятность использования
1, 2, 3, 4		0,3
1, 2, 3, 7		0,2
1, 2, 4, 7		0,2
1, 3, 4, 7		0,2
2, 3, 4, 7		0,1
Итого

Таблица 3.4. Выбор стратегий, которые использовал студент, когда действовал как второй игрок

Стратегия вытаскивания монет	Число раз использования	Вероятность использования
		0,5
		0,5
Итого

7. Полученные результаты представляются преподавателю.

8. Проводится разбор итогов принятия решений студентами. Рассматриваемая ситуация соответствует антагонистическим играм, в которых выигрыш первого игрока равен проигрышу второго, т.е.

F(i,j) = F₁(i,j)= - F₂(i,j)

где F₁(i,j) – выигрыш первого игрока при выборе им i-ой стратегии и 2-м игроком j-ой стратегии; F₂(i,j) – выигрыш второго при выборе первым i-ой стратегии и 2-м игроком j-ой стратегии. Таким образом, формируется матрица выигрыша, называемая платежной матрицей. Всего имеется 5 комбинаций монет, которые могут быть положены в контейнер первым игроком. Второй игрок, теоретически может использовать 12 комбинаций, при вытаскивании 2-х монет, и 4 комбинации при вытаскивании из контейнера 3-х монет. Но так как монеты различаются по размеру, то в случае вытаскивания 2-х монет он будет выбирать 2 наиболее крупные, а при вытаскивании 3-х монет – три наиболее мелкие.

Если стоимость вытягивания третьей монеты равна 4 единицам, то платежная матрица выглядит следующим образом

Стратегии 1-го игрока Комбинация монет	№ стратегии 1-го игрока	Стратегии 2-го игрока
Вытаскивание 2-х монет	Вытаскивание 3-х монет
1, 2, 3, 4			-6
1, 2, 3, 7		-6,5
1, 2, 4, 7		-7
1, 3, 4, 7		-7,5
2, 3, 4, 7			-12

В бескоалиционных играх принципом оптимальности является ситуация равновесия, которая в случае антагонистических игр означает наличие такой стратегии i* у первого игрока, и стратегии j* у второго игрока при которой соблюдается равенство

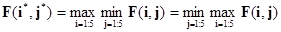
В нашем случае это равенство не соблюдается, так как

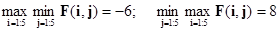
Для бескоалиционных игр с конечным числом стратегий существует ситуация равновесия в смешанных стратегиях Поиск равновесной смешанной стратегии Р₁ для 1-го игрока сводится к решению задачи линейного программирования:

A. 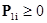для любой стратегии i, имеющейся у 1-го игрока

B..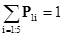

C. для любой стратегии j, имеющейся у 2-го игрока

D.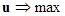

В случае наличия у 2-го игрока только двух стратегий решение этой задачи может быть получено графически.

Построим зависимость выигрыша 1-го игрока при выборе i-ой стратегии от выбора вторым игроком своей 1-ой стратегии (Р₂₁)

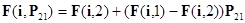
На рис. 3.1. показано изменение выигрыша 1-го игрока в зависимости от выбора смешанной стратегии вторым игроком

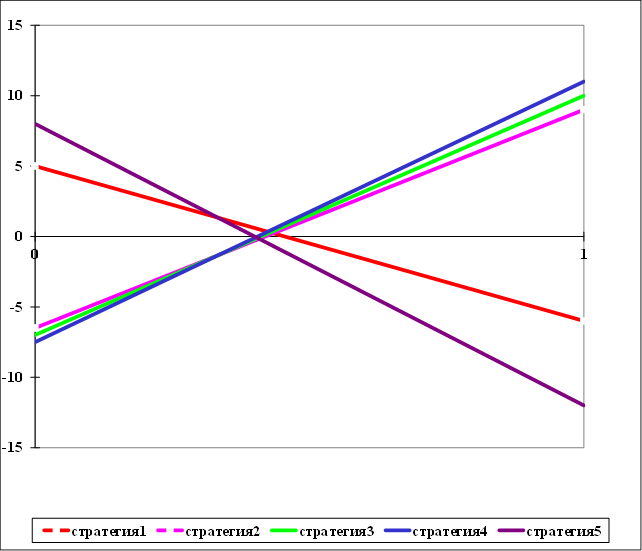
Рис. 3.1. Изменение выигрыша 1-го игрока в зависимости от выбора смешанной стратегии вторым игроком

Рассматривается верхняя огибающая и находится точка, в которой верхняя огибающая достигает своего минимума. Минимум достигается на пересечении 1-ой и 4-ой стратегий 1- го игрока. В этой точке вероятность выбора 2-м игроком своей первой стратегии равна - 0,576, а второй - 0,424. В случае 10 раундов 2-ой игрок должен 6 раз выбирать стратегию по вытягиванию 2-х монет и 4 раза по вытягиванию 3-х монет.

Первый игрок должен выбирать только 1-ую и 4-ую стратегии, так как при оптимальном выборе 2-м игроком своей оптимальной стратегии в любом другом случае он будет проигрывать больше.

Для нахождения равновесной стратегии 1-го игрока требуется приравнять

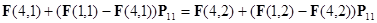(3.1.)

В нашем случае выбор первым игроком своей 1-ой стратегии (P₁₁) равен 0,627. Выбор первым игроком своей 4-ой стратегии равен 1-P₁₁ =0,373. В случае 10 раундов 1-ый игрок должен 6 раз выбирать стратегию по формированию комбинации монет (1,2,3,4) и 4 раза комбинацию (1,3,4,7).

9. После нахождения смешанных равновесных стратегий находится значение игры, т.е. тот выигрыш, который должен получить первый игрок при правильном выборе смешанной стратегии. Для этого достаточно подставить найденное значение P₁₁ в уравнение (3.1). В нашем примере гарантированный выигрыш первого игрока составляет 0,339.

10. Оцените, насколько Ваш выбор стратегий совпал с результатами, полученными с помощью математических моделей принятия решений. Укажите, какие причины сказались на отклонении Ваших решений от полученных с помощью математических методов.

11. Обобщить все полученные результаты и оформить их в виде отчета

Лабораторная работа №4. Деловая игра «Альянс» (Принятие решений в условиях сотрудничества)

1. Лабораторная работа проводится в форме деловой игры. Студенческая группа разбивается на команды по 3 человека. Нормальное число групп 5. Каждой команде выдается одинаковое задание.

2. В качестве задания рассматривается следующая ситуация: Каждый из участников группы представляет интересы разных компаний, действующих на едином рынке и выпускающих машиностроительную продукцию длительного пользования (например, автомобили). Они могут объединить свои усилия, создав альянс. В результате кооперирования появляется дополнительная прибыль, связанная с уменьшением затрат на разработку платформ изделий, сбыт продукции, а также пост продажное обслуживание. В таблице 4.1. показаны выгоды компаний, получаемые в результате объединения в единый альянс, а также в локальные группы

Таблица 4.1. Основные параметры выгод, получаемых от альянса компаний

	Выручка	Себестоимость производства	Расходы на сбыт	Расходы на пост продажное обслуживание	Расходы на НИОКР	Чистая прибыль
Компания 1
Компания 2
Компания 3
Альянс Ком-паний 1 и 2
Альянс Ком-паний 1 и 3
Альянс Ком-паний 2 и 3
Альянс Ком-паний 1, 2 и 3

3. Каждая группа сначала определяет выгоды, получаемые от создания альянса, а затем формирует предложения по распределению полученного дополнительного выигрыша. Дополнительный выигрыш определяется как кредитного капитала банков с учетом инфляции на конец периода.

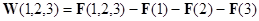
Где F(1,2,3) – Чистая прибыль получаемая альянсом, F(i) – чистая прибыль, получаемая i-ой компанией индивидуально.

4. Из представителей 5 групп формируются 3 «заводских» команды. В каждой команде выбирается руководитель. Под его председательством обсуждаются предложения, сделанные в отдельных группах. Вырабатывается стратегия команды на завершающие переговоры, которые проводят руководители каждой из команд.

5. Выбранное решение представляется всем участникам игры. Каждый из руководителей команд представляет доклад, объясняющий, почему компания согласилась, на ту долю общей прибыли, которая в конечном итоге была определена команде на заключительных переговорах.

6. Найденное решение проверяется преподавателем. Исходная ситуация является примером классической кооперативной игры трех лиц. Первой задачей является нахождение множества дележей, которое показывает все возможные варианты распределения, полученного общей коалицией G выигрыша между игроками. Дележ Х=(Х1,Х2,Х3) полученной в общей коалиции чистой прибыли отвечает двум условиям:

1. Индивидуальной рациональности Х_L >= F (L) для каждого игрока L, т.е. в общей коалиции каждый игрок может получить не меньше, чем, действуя самостоятельно.

2. Коллективной рациональности å Х_L= F(G), т.е. весь выигрыш

LÎ G

полученный общей коалицией G должен быть распределен между участниками.

7. Основным подходом к определению рациональных дележей является нахождение С -ядра (от английского Core) игры. Считается, что дележ Х принадлежит С -ядру, если дополнительно к перечисленным выше условиям, он отвечает условию групповой рациональности, которое формулируется как

å Х_L>= F (К), для любой коалиции К.

 LÎ K

Условие групповой рациональности означает, что, действуя в рамках общей коалиции, каждый игрок получает не меньше, чем при образовании какой-то сепаратной коалиции. Дележи, входящие в С -ядро, называются устойчивыми дележами, так как ни один из игроков не может отклониться от предлагаемого распределения, расколов общую коалицию.

В кооперативной игре 3-х лиц С-ядро можно построить графически, используя так называемые барицентрические координаты.

8. Для графического построения С-ядра используют так называемую 0-1 редуцированную форму игры. Выигрыш в этой форме определяется по формуле:

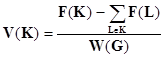
В этой форме V(1)=V(2)=V(3)=0 и V(1,2,3)=1. Значения для локальных коалиций в нашем примере равны

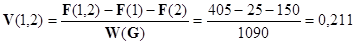
Аналогично рассчитанные V(1,3) = 0,523 и V(2,3) =0,798.

В барицентрических координатах, дележ, соответствующий передаче всего совместного выигрыша 1-му игроку соответствует вершине 1, передаче всего совместного выигрыша 2-му игроку соответствует вершине 2, передаче всего совместного выигрыша 3-му игроку соответствует вершине 3. Нулевой выигрыш 1-го находится на стороне противолежащей вершине 1, нулевой выигрыш 2-го находится на стороне противолежащей вершине 2, нулевой выигрыш 3-го находится на стороне противолежащей вершине 3.

Для построения линии, которая соответствует V(1,2) =0,211 необходимо построить отрезок прямой, на которой X₃=1-V(1,2). Для построения линии, которая соответствует V(1,3) =0,523 необходимо построить отрезок прямой, на которой X₂=1-V(1,3). Для построения линии, которая соответствует V(2,3) =0,798 необходимо построить отрезок прямой, на которой X₁=1-V(2,3).

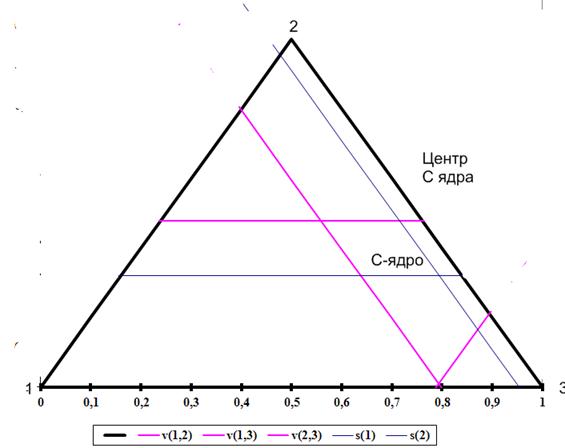
Рис.1 Множество дележей и центр С-ядра.

В С-ядре обычно бывает достаточно много дележей, поэтому стараются найти центр С-ядра, под которым понимают наиболее устойчивую точку С-ядра. Для 3-х участников его параметры находятся с помощью следующих формул:

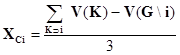(4.1)

Если для одной из компонент, рассчитанной по формуле (4.1) значение Х_Сi оказывается отрицательным, то значение этой компоненты полагается равным 0, а значение других компонент рассчитывается по формуле

В нашем случае центр ядра имеет координаты X_C1 = 0,046, X_C2 =0,321; Х_С3= 0,633

9. Следующим шагом является расчет того совокупного выигрыша, который получит каждый из игроков:

(4.2)

В нашем случае выигрыш 1-го участника альянса равняется У_C1 =25+ 0,046*1090=75, У_C2 =150+0,321*1090 =500; У_С3= 525+0,633*1090=1215.

Центр С-ядра является наиболее устойчивым, но не самым справедливым. Наиболее известным вариантом справедливого дележа является вектор Шепли (Shapley), в основу которого положены следующие аксиомы:

1. Независимости от названия (имени). Величина доли выигрыша каждого игрока зависит только от его потенциального вклада в действия любой из коалиций, которая может быть создана с его участием, а не от номера или названия.

2. Независимость от сторонних выигрышей (Отсутствие зависти). Величина доли выигрыша в данной игре не зависит от размеров выплат, получаемых игроком в других играх.

3. Принцип болвана (бесполезного игрока). Игрок, включение которого в любую коалицию не дает больше, чем прибавление его индивидуальный выигрыша, называется болваном. Болван должен получить ровно столько, сколько он может получить, действуя индивидуально.

Дата добавления: 2014-12-23